Đề bài
Sử dụng các thông tin và hình 107 để trả lời các câu hỏi sau:
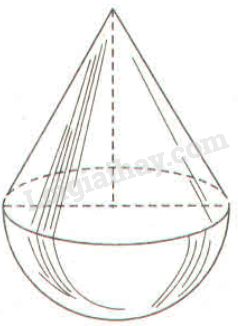
Một đồ chơi “lắc lư” của trẻ em gồm một hình nón gắn với nửa hình cầu (h.107) (chiều cao của hình nón bằng đường kính đường tròn đáy). Có hai loại đồ chơi: loại thứ nhất cao \(9cm\), loại thứ hai cao \(18cm\).
a) Tỉ số: \(\displaystyle{\text{thể tích đồ chơi loại thứ hai} \over \text{thể tích đồ chơi loại thứ nhất}}\)
(A) \(2\) (C) \(8\)
(B) \(4\) (D) \(16\)
Hãy chọn kết quả đúng.
b) Trong các số sau đây:
(A) \(2 (cm)\) (C) \(4 (cm)\)
(B) \( 3 (cm)\) (D) \(\displaystyle 4{1 \over 2}(cm)\)
Số nào là bán kính đường tròn đáy của đồ chơi loại thứ nhất?
c) Trong các số sau đây:
(A) \(30\pi \left( {c{m^3}} \right)\) (B) \(36\pi \left( {c{m^3}} \right)\)
(C) \(72\pi \left( {c{m^3}} \right)\) (D) \(610\left( {c{m^3}} \right)\)
Số nào là thể tích của loại đồ chơi thứ nhất?
Phương pháp giải - Xem chi tiết
Sử dụng:
- Thể tích hình nón có bán kính đáy \(r\), chiều cao \(h\) là: \(V = \dfrac{1}{3}\pi {r^2}h\).
- Thể tích hình cầu bán kính \(r\) là: \(\displaystyle V ={4 \over 3}\pi {r^3}\).
Lời giải chi tiết
a) Loại thứ nhất có chiều cao \(9cm\) là bao gồm chiều cao của hình nón và bán kính của hình cầu, mà chiều cao hình nón bằng đường kính hình cầu.
Gọi \(r\) là bán kính của hình cầu ta có:
\(2r + r = 9 \Rightarrow r = 3\left( {cm} \right)\)
Chiều cao hình nón là: \(h=2r = 6\,cm\)
Thể tích hình nón là: \({V_1} = \displaystyle {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {.3^2}.6 = 18\pi \) \(\left( {c{m^3}} \right)\)
Thể tích nửa hình cầu là: \(\displaystyle {V_2} = {1 \over 2}.{4 \over 3}\pi {.3^3} = 18\pi \left( {c{m^3}} \right)\)
Thể tích loại đồ chơi thứ nhất là: \(18\pi+18\pi=36\pi \left( {c{m^3}} \right)\)
Loại thứ 2 có chiều cao \(18cm\) là bao gồm chiều cao hình nón và bán kính hình cầu mà chiều cao hình nón bằng đường kính hình cầu.
Gọi \(R\) là bán kính của hình cầu ta có:
\(2R + R = 18 \Rightarrow R = 6\,cm\)
Chiều cao hình nón là: \(h'=2R = 12\,cm\)
Thể tích hình nón là: \(\displaystyle {V_1}' = {1 \over 3}\pi {R^2}.h' = {1 \over 3}\pi {.6^2}.12 = 144\pi \) \(\left( {c{m^3}} \right)\)
Thể tích nửa hình cầu là: \(\displaystyle {V_2}' = {1 \over 2}.{4 \over 3}\pi {R^3} = {1 \over 2}.{4 \over 3}\pi {.6^3} = 144\pi \) \(\left( {c{m^3}} \right)\)
Thể tích loại đồ chơi thứ 2 là: \(144\pi +144\pi =288\pi \left( {c{m^3}} \right)\)
\(\displaystyle{\text{thể tích đồ chơi loại thứ hai} \over \text{thể tích đồ chơi loại thứ nhất}}\) \(\displaystyle = {{288\pi } \over {36\pi }} = 8\)
Chọn (C).
b) Bán kính đường tròn đáy đồ chơi thứ nhất là \(r=3\,cm\).
Chọn (B).
c) Thể tích loại đồ chơi thứ nhất là: \(18\pi+18\pi=36\pi \left( {c{m^3}} \right)\).
Chọn (B).
soanvan.me
