Đề bài
Cho các hình thoi \(ABCD\) có cạnh \(AB\) cố định. Tìm quỹ tích giao điểm \(O\) của hai đường chéo của các hình thoi đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)
Lời giải chi tiết
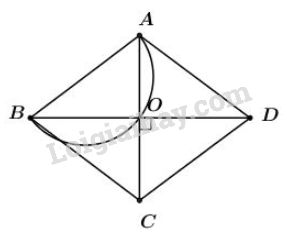
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.
Chứng minh:
Phần thuận:
Vì ABCD là hình thoi nên \(AC \bot BD\) tại \(O.\) (Tính chất)
Vậy điểm \(O\) nhìn \(AB\) cố định dưới góc \(90^0.\)
\(\Rightarrow \) Quỹ tích điểm \(O\) là nửa đường tròn đường kính \(AB.\)
Phần đảo:
Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.
+ Lấy điểm O thuộc nửa đường tròn đường kính AB
+ Lấy C đối xứng với A qua O
+ Lấy D đối xứng với B qua O.
Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường
⇒ ABCD là hình bình hành (Dấu hiệu nhận biết)
Mà O thuộc nửa đường tròn đường kính AB
\(⇒ \widehat {AOB} = {90^0}\)
⇒ AC ⊥ DB
⇒ Hình bình hành ABCD là hình thoi (Hình bình hành có 2 đường chéo vuông góc)
Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)
soanvan.me
