Đề bài
Gọi cung chứa góc \(55^0\) ở bài tập 46 là \(\overparen{AmB}\). Lấy điểm \({M_1}\) nằm bên trong và điểm \({M_2}\) nằm bên ngoài đường tròn chứa cung này sao cho \({M_1},{M_2}\) và cung \(\overparen{AmB}\) nằm cùng về một phía đối với đường thẳng \(AB\). Chứng minh rằng:
a) \(\widehat {A{M_1}B} > 55^0\);
b) \(\widehat {A{M_2}B} < 55^0\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng:
+ Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn
+ Số đo của góc có đỉnh bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn
Lời giải chi tiết
a) \({M_1}\) là điểm bất kì nằm trong cung chứa góc \(55^0\) (hình vẽ).

Gọi \(A', \, B’\) theo thứ tự là giao điểm của \({M_1}A,\) \({M_1}B\) với cung tròn.
Ta có \(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(\overparen{AB} = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))
Vì \(\widehat{A{M_1}B}\) là góc có đỉnh nằm trong đường tròn chắn cung \(A'B'\) và \(AB\) nên:
\(\widehat {A{M_1}B}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{A'B'}}{2}>\dfrac {1}{2}sđ\overparen{AB} =55^0\).
Vậy \(\widehat {A{M_1}B} > 55^0\)
b) \({M_2}\) là điểm bất kì nằm ngoài đường tròn (hình vẽ )
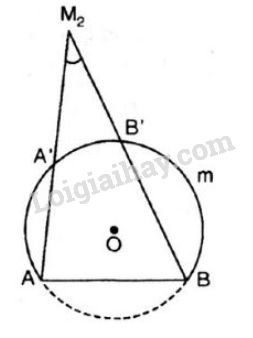
Ta có \({M_2}A, \, {M_2}B\) lần lượt cắt đường tròn tại \(A’, \, B’.\)
\(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(AB = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))
Vì góc \(\widehat {A{M_2}B}\) là góc có đỉnh nằm bên ngoài đường tròn chắn cung \(A'B'\) và \(AB\) nên:
\(\widehat {A{M_2}B}= \dfrac{sđ\overparen{AB}-sđ\overparen{A'B'}}{2}<\dfrac {1}{2}sđ\overparen{AB} =55^0 .\)
Vậy \(\widehat {A{M_2}B} < 55^0.\)
soanvan.me
