Đề bài
Dựng tam giác \(ABC,\) biết \(BC = 6cm,\) \(\widehat{A}=40^0\) và đường cao \(AH = 4cm.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựng cung chứa góc \(40^\circ \) trên cạnh \(BC\).
Vẽ đường thẳng song song với \(BC\) và cách \(BC\) khoảng \(4cm\).
Từ đó xác định điểm \(A\) và tam giác \(ABC.\)
Lời giải chi tiết
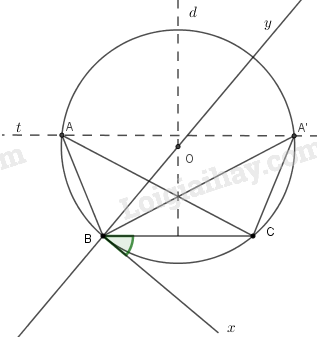
Cách dựng:
+ Kẻ đoạn thẳng \(AB = 6cm\)
+ Dựng cung chứa góc \(40^\circ \) trên đoạn \(BC.\)
- Vẽ đường trung trực d của đoạn \(BC\)
- Vẽ tia \(Bx\) tạo với \(BC\) góc \(40^\circ \)
- Vẽ tia \(By \bot Bx\), tia \(By\) cắt đường thẳng \(d\) tại \(O.\) Vẽ cung \(BmC\) tâm \(O\) bán kính \(OB\) sao cho cung này nằm ở nửa mặt phẳng bờ \(BC\) không chứa \(Bx\). Cung \(BmC\) chính là cung chứa góc \(40^\circ \) cần dựng.
+ Vẽ đường thẳng \(t\) song song với \(BC\) và cách \(BC\) một khoảng \(4cm.\) Gọi giao điểm của đường thẳng \(t\) với cung \(BmC\) là \(A\) và \(A'.\)
Khi đó có hai tam giác thỏa mãn đề bài là \(ABC\) hoặc tam giác \(A'BC.\)
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
\(\Rightarrow \widehat {BAC} = {40^0}\)
+ A ∈ t song song với BC và cách BC 4cm nên chiều cao của tam giác ABC là 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận:
Vì t cắt cung \(BmC\) tại 2 điểm nên bài toán có 2 nghiệm hình
