Đề bài
Cho hai điểm \(A, B\) cố định. Từ \(A\) vẽ các tiếp tuyến với đường tròn tâm \(B\) bán kính không lớn hơn \(AB\). Tìm quỹ tích các tiếp điểm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)
Lời giải chi tiết
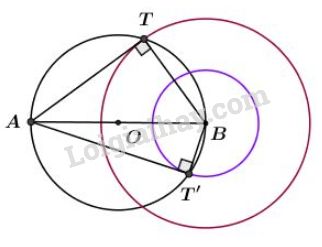
Dự đoán: Quỹ tích là đường tròn đường kính AB.
+ Phần thuận:
Tiếp tuyến \(TA\) vuông góc với bán kính \(BT\) tại tiếp điểm \(T\).
Suy ra \( \widehat{ATB}=90^0\)
Do \(AB\) cố định nên quỹ tích của \(T\) là đường tròn đường kính \(AB\).
+ Phần đảo:
Lấy T thuộc đường tròn đường kính AB
\( \Rightarrow \widehat {ATB} = {90^0}\) ( Góc nội tiếp chắn nửa đường tròn)
⇒ AT ⊥ TB và BT < AB
⇒ AT tiếp xúc với đường tròn tâm B, bán kính BT < BA.
Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB.
