Đề bài
Cho mạch điện có sơ đồ như hình 6.6, trong đó các điện trở R1=14Ω; R2=8Ω; R3=24Ω; dòng điện đi qua R1 có cường độ là I1=0,4A
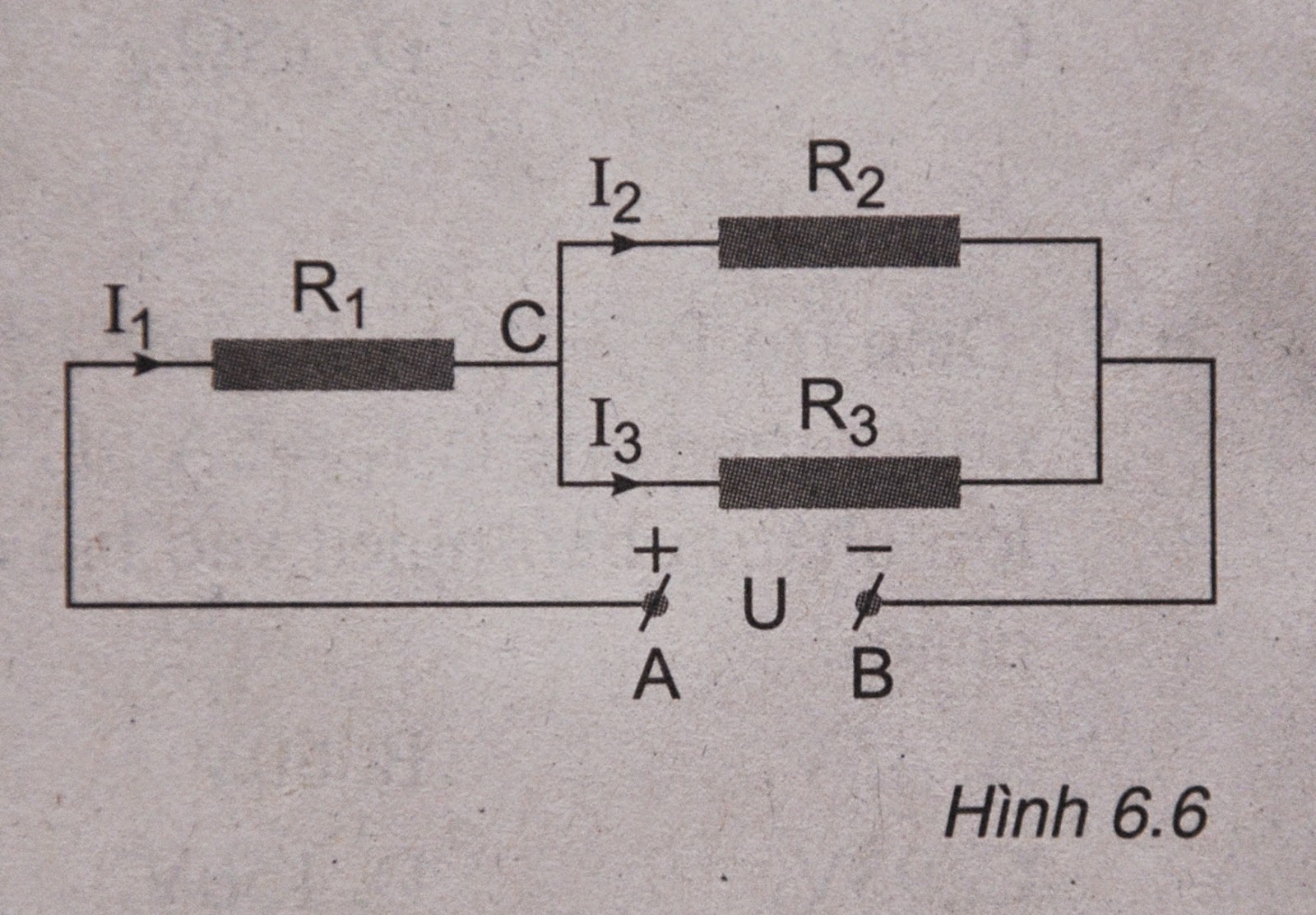
a. Tính cường độ dòng điện I2, I3 tương ứng đi qua các điện trở R2 và R3.
Phương pháp giải - Xem chi tiết
+ Sử dụng biểu thức: \(U=I.R\)
+ Sử dụng biểu thức tính điện trở tương đương của đoạn mạch có các điện trở mắc song song: \(\dfrac{1}{R_{23}} = \dfrac{1}{R_2} + \dfrac{1}{R_3}\)
Lời giải chi tiết
a)
Mạch gồm: \(R_1\) nt [\(R_2\)//\(R_3\)]
Ta có:
\(\dfrac{1}{R_{23}} = \dfrac{1}{R_2} + \dfrac{1}{R_3} =\dfrac{1}{8} + \dfrac{1}{24} \\\Rightarrow {R_{23}} = 6\Omega \)
\(R_{tđ}= R_1 + R_{23} = 14 + 6 = 20Ω\)
Do \(R_1 nt R_{23}\)
nên \( I_1 = I_{23} = 0,4A\)
\(U_{23} = I_{23} .R_{23}= 0,4.6 = 2,4V\\⇒ U_{23}= U_2= U_3 = 2,4 V\) (do \(R_2 // R_3\))
\({I_2} = \dfrac{U_2}{R_2} = \dfrac{2,4}{8} = 0,3{\rm{A}};\\{I_3} = \dfrac{U_3}{R_3} = \dfrac{2,4}{24} = 0,1{\rm{A}}\)
b)
\(U_{AB} = I.R = 0,4.20 = 8V\)
\(U_{AC}= I_1.R_1 = 0,4.14 = 5,6V\)
\(U_{CB}= I_{23}.R_{23} = 0,4.6 = 2,4V\)
soanvan.me
