Đề bài
Hãy chia hình thang ABCD thành hai hình thang có diện tích bằng nhau.
Lời giải chi tiết
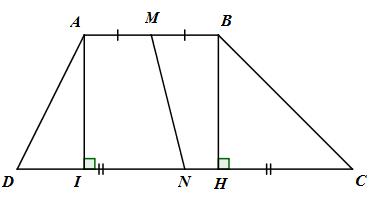
Gọi M, N lần lượt là trung điểm của AB và CD.
Kẻ \(AI \bot CD\) tại I, \(BH \bot CD\) tại H
Tứ giác ABHI có:
AI // BH (cùng vuông góc với CD) và
AB // IH (AB // CD, \(I \in CD\))
\( \Rightarrow \) Tứ giác ABHI là hình hình hành \( \Rightarrow AI = BH\)
Ta có: \({S_{AMND}} = {{\left( {AM + DN} \right).AI} \over 2};\,\,\,{S_{MBCN}} = {{\left( {MB + NC} \right).BH} \over 2}\)
\(AM = MB\) (M là trung điểm của AB)
\(DN = NC\) (N là trung điểm của CD)
\(AI = BH\)
Do đó \({S_{AMND}} = {S_{MBCN}}\)
soanvan.me
