Đề bài
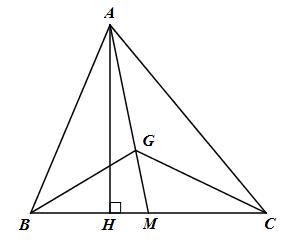
Cho tam giác ABC có G là trọng tâm. BC = 42 cm và chiều cao AH = 10 cm. Tính diện tích tam giác GBC.
Lời giải chi tiết
\({S_{ABC}} = {1 \over 2}BC.AH = {1 \over 2}.42.10 = 210\,\,\left( {c{m^2}} \right)\)
Gọi M là giao điểm của AG và BC.
Vì G là trọng tâm của tam giác ABC (gt)
\( \Rightarrow AG = {2 \over 3}AM \Rightarrow GM = {1 \over 2}AM\)
Ta có \({S_{GBM}} = {1 \over 3}{S_{ABM}}\) (chung đường cao vẽ từ C đêbs AM và \(GM = {1 \over 3}AM\))
Do đó \({S_{GBC}} = {S_{GBM}} + {S_{GCM}} = {1 \over 3}{S_{ABM}} + {1 \over 3}{S_{ACM}} = {1 \over 3}{S_{ABC}} = {1 \over 3}.210 = 70\,\,\left( {c{m^2}} \right)\)
soanvan.me
