Đề bài
Tính theo a diện tích của hình thoi có bốn cạnh cà một đường chéo cùng bằng a.
Lời giải chi tiết
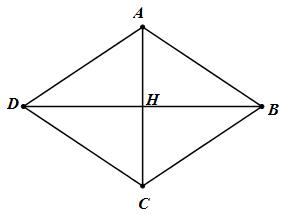
Gọi H là giao điểm của AC và BD. Tứ giác ABCD là hình thoi
\( \Rightarrow H\) là trung điểm của AC và BD \( \Rightarrow AH = {{AC} \over 2} = {a \over 2}\)
\(AC \bot DB\) tại H (ABCD là hình thoi) \( \Rightarrow \Delta AHD\) vuông tại H.
\( \Rightarrow D{H^2} + A{H^2} = A{D^2}\) (định lí Pytago)
\( \Rightarrow D{H^2} + {{{a^2}} \over 4} = {a^2} \Rightarrow D{H^2} = {a^2} - {{{a^2}} \over 4} = {{3{a^2}} \over 4}\)
\( \Rightarrow DH = {{a\sqrt 3 } \over 2} \Rightarrow DB = 2DH = {{2.a\sqrt 3 } \over 2} = a\sqrt 3 \) (do H là trung điểm của DB)
\({S_{ABCD}} = AC.DB = a.a\sqrt 3 = {a^2}\sqrt 3 \,\,\left( {dvdt} \right)\)
soanvan.me
