Đề bài
Tính các góc của một hình bình hành có diện tích bằng 60 cm2 và hai cạnh bên của góc nhọn có độ dài là 100 cm và 12 cm.
Lời giải chi tiết
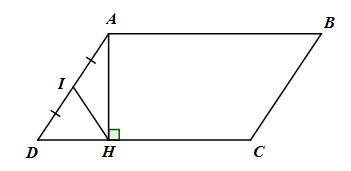
Kẻ đường cao AH của hình bình hành ABCD
\({S_{ABCD}} = AH.AB \Rightarrow 60 = AH.12 \Rightarrow AH = 5\,\,\left( {cm} \right)\)
Gọi I là trung điểm của AD
\(\Delta ADH\) vuông tại H có HI là đường trung tuyến (I là trung điểm của AD)
\( \Rightarrow HI = AI = {{AD} \over 2} = {{10} \over 2} = 5\,\,\left( {cm} \right)\)
Mà \(AH = 5cm\) nên \(HI = AI = AH \Rightarrow \Delta AHI\) đều \( \Rightarrow \widehat {IAH} = {60^0}\)
Mà \(\widehat {ADH} + \widehat {IAH} = {90^0}\,\,(\Delta ADH\) vuông tại H)
Nên \(\widehat {ADH} + {60^0} = {90^0} \Rightarrow \widehat {ADH} = {30^0} \Rightarrow \widehat {ADC} = {30^0}\)
Lại có \(\widehat {ABC} = \widehat {ADC}\) (ABCD là hình bình hành) do đó \(\widehat {ABC} = \widehat {ADC} = {30^0}\)
Ta có: \(\widehat {ADC} + \widehat {DAB} = {180^0}\) (hai góc trong cùng phía và AB // CD)
\( \Rightarrow {30^0} + \widehat {DAB} = {180^0} \Rightarrow \widehat {DAB} = {180^0} - {30^0} = {150^0}\)
Mà \(\widehat {BCD} = \widehat {DAB}\) (ABCD là hình bình hành) nên \(\widehat {BCD} = \widehat {DAB} = {150^0}\)
soanvan.me
