Đề bài
Chứng minh hai đường chéo của một hình bình hành luôn chia nó thành bốn tam giác có diện tích bằng nhau.
Lời giải chi tiết
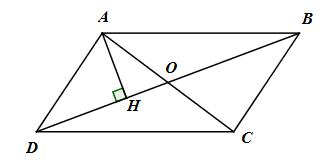
Gọi O là giao điểm của AC và BD, kẻ \(AH \bot DB\) tại H.
ABCD là hình bình hành \( \Rightarrow O\) là trung điểm của AC và BD.
Ta có \({S_{ADO}} = {1 \over 2}AH.DO,\,\,{S_{ABO}} = {1 \over 2}AH.BO\)
Và \(DO = OB\) (O là trung điểm của BD)
Do đó \({S_{ADO}} = {S_{ABO}}\)
Lập luận tương tự ta có : \({S_{ADO}} = {S_{CDO}},\,\,{S_{CDO}} = {S_{BCO}}\)
Vậy \({S_{ADO}} = {S_{ABO}} = {S_{BCO}} = {S_{CDO}}\)
soanvan.me
