Đề bài
Cho tam giác ANC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Lời giải chi tiết
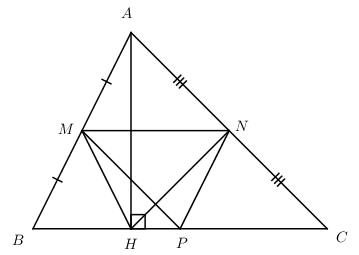
Xét tam giác ABC ta có:
M là trung điểm của AB (gt) ;
N là trung điểm của AC (gt) ;
\( \Rightarrow MN\) là đường trung bình của tam giác ABC \( \Rightarrow MN//BC\)
\( \Rightarrow \) Tứ giác MNPH là hình thang.
Xét tam giác ABC ta có :
M là trung điểm của AB (gt) ;
P là trung điểm của BC
\( \Rightarrow MP\) là đường trung bình của tam giác ABC \( \Rightarrow MP = {1 \over 2}AC\)
\(\Delta ACH\) vuông tại H có HN là trung tuyến (N là trung điểm của AC)
\( \Rightarrow NH = {1 \over 2}AC\). Mà \(MP = {1 \over 2}AC\,\,\left( {cmt} \right)\)
\( \Rightarrow NH = MP\)
Hình thang MNPH (MN//PH) có \(MP = NH\) nên là hình thang cân.
Nhận xét : Đề bài cần bổ sung thêm \(AB < AC\)
soanvan.me
