Đề bài
Cho hình thang cân ABCD (AB//CD) có đường chéo AC vuông góc với cạnh bên AD và AB = BC = 3 cm.
a) Có nhận xét gì về tam giác ACD, chứng minh điều đó. Tính các góc của tam giác ACD và của hình thang cân ABCD.
b) Nêu cách dựng hình thang cân ABCD.
Lời giải chi tiết
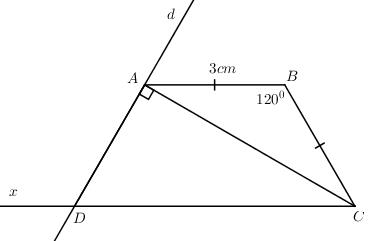
a) Ta có \(\widehat {BAC} = \widehat {ACD}\) (so le trong AB // CD)
Mặt khác \(AB = BC\,\,\left( {gt} \right) \Rightarrow \Delta ABC\) cân tại B \( \Rightarrow \widehat {BAC} = \widehat {BCA}\)
Do đó \(\widehat {BAC} = \widehat {ACD} = \widehat {BCA}\)
Nên \(\widehat {ABC} = \widehat {BAD} = \widehat {CAD} + \widehat {BAC} = {90^0} + \widehat {ACD}\)
Mặt khác \(\widehat {ABC} + \widehat {BCD} = {180^0}\) (hai góc trong cùng phía và AB // CD)
Nên \({90^0} + \widehat {ACD} + \widehat {ACD} + \widehat {ACD} = {360^0} \Rightarrow 3\widehat {ACD} = {90^0} \Rightarrow \widehat {ACD} = {30^0}\)
\(\Delta ACD\) vuông tại A có \(\widehat {ACD} = {30^0}\)
Và \(\widehat {ADC} = {90^0} - \widehat {ACD} = {90^0} - {30^0} = {60^0}\)
Do đó \(\widehat {BAD} = \widehat {ABC} = {90^0} + \widehat {ACD} = {120^0}\)
\(\widehat {ADC} = \widehat {BCD} = \widehat {ACD} + \widehat {BCA} = {60^0}\)
b) Cách dựng
- Dựng tam giác ABC cân tại B có \(AB = BC = 3cm,\,\,\widehat {ABC} = {120^0}\)
- Dựng tia Cx//AB (tia Cx và A cùng nằm trên nửa mặt phẳng bờ BC)
- Dựng đường thẳng d qua A và vuông góc với AC, D là giao điểm của d và tia Cx.
Tứ giác ABCD là hình thang cân cần dựng.
Chứng minh
\(\Delta ABC\) cân tại B, \(\widehat {ABC} = {120^0}\) (bước dựng 1)
\( \Rightarrow \widehat {BAC} = \widehat {BCA} = \left( {{{180}^0} - \widehat {ABC}} \right):2 = {30^0}\)
\(\widehat {DAC} = {90^0}\,\,\left( {d \bot AC} \right)\)
Nên \(\widehat {BAD} = \widehat {DAC} + \widehat {BAC} = {90^0} + {30^0} = {120^0}\)
Ta có AB // CD (Vì Cx // AB) \( \Rightarrow \) Tứ giác ABCD là hình thang.
Mà \(\widehat {BAD} = \widehat {ABC}\,\,\left( { = {{120}^0}} \right)\). Do đó ABCD là hình thang cân.
Vậy tứ giác ABCD là hình thang cân
(AB // CD) có \(AB = BC = 3cm,\,\,AC \bot AD\)
soanvan.me
