Đề bài
Cho hình thang ABCD (AB và CD là hai đáy và AB < CD), AD = BC = AB, \(\widehat {BDC} = {30^o}\) .
Tính các góc của hình thang.
Lời giải chi tiết
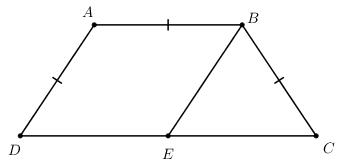
Ta có \(AD = AB\,\,\left( {gt} \right) \Rightarrow \Delta ABD\) cân tại A \( \Rightarrow \widehat {ADB} = \widehat {ABD}\)
Mà \(\widehat {ABD} = \widehat {BDC}\) (so le trong và AB // CD) và \(\widehat {BDC} = {30^0}\,\,\left( {gt} \right)\) nên \(\widehat {ADB} = \widehat {ABD} = {30^0}\)
Ta có \(\widehat {ADC} = \widehat {ADB} + \widehat {BDC} = {30^0} + {30^0} = {60^0}\)
\(\widehat {BAD} + \widehat {ADC} = {180^0}\) (hai góc trong cùng phía và AB // CD)
Do đó \(\widehat {BAD} + {60^0} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {60^0} = {120^0}\)
Trên cạnh CD lấy điểm E sao cho \(DE = AB\)
Hình thang ABED \(\left( {AB//DE} \right)\) có \(AB = DE\)
\( \Rightarrow BE//AD\) và \(BE = AD\)
\(BE = BC\,\,\left( { = AD} \right) \Rightarrow \Delta BEC\) cân tại B \( \Rightarrow \widehat {BEC} = \widehat {BCD}\)
Mặt khác \(\widehat {BEC} = \widehat {ADC}\) (đồng vị và AD // BE)
Do đó \(\widehat {BCD} = \widehat {ADC} = {60^0}\)
Mặt khác \(\widehat {ABC} + \widehat {BCD} = {180^0}\) (hai góc trong cùng phía và AB // CD)
Do đó \(\widehat {ABC} = {180^0} - \widehat {BCD} = {180^0} - {60^0} = {120^0}\)
soanvan.me
