Đề bài
Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng mình rằng BN = MN.
Lời giải chi tiết
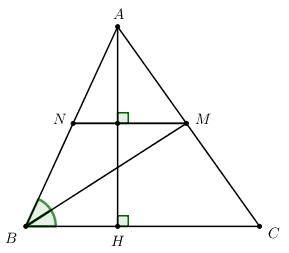
a) Ta có: \(MN \bot AH\,\,\left( {gt} \right)\)
Và \(BC \bot AH\) (AH là đường cao của tam giác ABC) \( \Rightarrow MN//BC \Rightarrow \widehat {BMN} = \widehat {CBM}\)( so le trong)
Và \(\widehat {NBM} = \widehat {MBC}\) (BM là tia phân giác góc B)
Suy ra \(\widehat {BMN} = \widehat {NBM} \Rightarrow \Delta BMN\) cân tại N.
Vậy \(BN = MN\)
soanvan.me
