Tích của đơn thức $x$ và đa thức $(1 – x)$ là:
-
A
\(1 - 2x\)
-
B
\(x - {x^2}\)
-
C
\({x^2} - x\)
-
D
\({x^2} + x\)
Đáp án của giáo viên lời giải hay : B
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
\(x\left( {1 - x} \right) = x.1 - x.x = x - {x^2}\)
Tích của đa thức \(4{x^5} + 7{x^2}\) và đơn thức \(\left( { - 3{x^3}} \right)\) là:
-
A
\(12{x^8} + 21{x^5}\)
-
B
\(12{x^8} + 21{x^6}\)
-
C
\( - 12{x^8} + 21{x^5}\)
-
D
\( - 12{x^8} - 21{x^5}\)
Đáp án của giáo viên lời giải hay : D
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
\(\left( {4{x^5} + 7{x^2}} \right).\left( { - 3{x^3}} \right) \)\(= 4{x^5}.\left( { - 3{x^3}} \right) + 7{x^2}.\left( { - 3{x^3}} \right) = - 12{x^8} - 21{x^5}\)
Rút gọn biểu thức \(A = \left( {{x^2} + 2 - 2x} \right)\left( {{x^2} + 2 + 2x} \right) - {x^4}\) ta được kết quả là:
-
A
\(A = 4\)
-
B
$A = - 4$
-
C
\(A = 19\)
-
D
\(A = - 19\)
Đáp án của giáo viên lời giải hay : A
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Hoặc sử dụng hằng đẳng thức $(a+b)(a-b)=a^2-b^2$ và $(a+b)^2=a^2+2ab+b^2$
$A = \left( {{x^2} + 2 - 2x} \right)\left( {{x^2} + 2 + 2x} \right) - {x^4} $$= {x^2}.{x^2} + 2.{x^2} + 2x.{x^2} + 2.{x^2} + 2.2 + 2.2x - 2x.{x^2} - 2.2x - 2x.2x - {x^4} $$=x^4+2x^2+2x^3+2x^2+4+4x-2x^3-4x-4x^2-x^4$$= 4$
Vậy $A = 4$.
Rút gọn đa thức \(16{x^2} - 4x + \dfrac{1}{4}\) ta được kết quả nào sau đây?
-
A
\({\left( {4x - \dfrac{1}{2}} \right)^2}\)
-
B
\({\left( {x - \dfrac{1}{2}} \right)^2}\)
-
C
\({\left( {4x + \dfrac{1}{2}} \right)^2}\)
-
D
\({\left( {x + \dfrac{1}{2}} \right)^2}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
\(16{x^2} - 4x + \dfrac{1}{4} = {\left( {4x} \right)^2} - 2.4x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {\left( {4x - \dfrac{1}{2}} \right)^2}\)
Trong các khai triển hằng đẳng thức sau, khai triển nào sai?
-
A
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
-
B
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B - 3A{B^2} + {B^3}\)
-
C
\({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)
-
D
\({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\)
Đáp án của giáo viên lời giải hay : B
\({\left( {A - B} \right)^3} \)\(= {\left( {A + \left( { - B} \right)} \right)^3} \)\(= {A^3} + 3.{A^2}.\left( { - B} \right) + 3.A.{\left( { - B} \right)^2} + {\left( { - B} \right)^3}\)\( = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
\( \Rightarrow {\left( {A - B} \right)^3} \)\(= {A^3} - 3{A^2}B - 3A{B^2} + {B^3}\) là sai.
Cho biết \(3{y^2} - 3y\left( {y - 2} \right) = 36\). Giá trị của $y$ là:
-
A
5
-
B
6
-
C
7
-
D
8
Đáp án của giáo viên lời giải hay : B
Biến đổi vế trái bằng cách sử dụng quy tắc nhân đơn thức với đa thức rồi cộng trừ các hạng tử đồng dạng
Từ đó tìm \(y.\)
\(\begin{array}{l}3{y^2} - 3y\left( {y - 2} \right) = 36\\ \Leftrightarrow 3{y^2} - 3y.y - 3y\left( { - 2} \right) = 36\\ \Leftrightarrow 3{y^2} - 3{y^2} + 6y = 36\\ \Leftrightarrow 6y = 36 \\\Leftrightarrow y = 6\end{array}\)
Giá trị của biểu thức \(A = 2x\left( {3x - 1} \right) - 6x\left( {x + 1} \right) - \left( {3 - 8x} \right)\) là:
-
A
\( - 16x - 3\)
-
B
\( - 3\)
-
C
\( - 16x\)
-
D
Đáp án khác
Đáp án của giáo viên lời giải hay : B
Sử dụng quy tắc nhân đơn thức với đa thức rồi cộng trừ các hạng tử đồng dạng
\(\begin{array}{l}\,\,\,\,\,\,\,A = 2x\left( {3x - 1} \right) - 6x\left( {x + 1} \right) - \left( {3 - 8x} \right)\\ \Leftrightarrow A = 2x.3x - 2x.1 - 6x.x - 6x.1 - 3 + 8x\\ \Leftrightarrow A = 6{x^2} - 2x - 6{x^2} - 6x - 3 + 8x\\ \Leftrightarrow A = - 3\end{array}\)
Thực hiện phép tính \(\left( {{x^2} + x + 1} \right)\left( {{x^3} - {x^2} + 1} \right)\) ta được kết quả là:
-
A
\({x^5} + x + 1\)
-
B
\({x^5} - {x^4} + x\)
-
C
\({x^5} + {x^4} + x\)
-
D
\({x^5} - x - 1\)
Đáp án của giáo viên lời giải hay : A
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
$\begin{array}{l}\;\;\;\left( {{x^2} + x + 1} \right)\left( {{x^3} - {x^2} + 1} \right)\\ = {x^2}.{x^3} - {x^2}.{x^2} + {x^2}.1 + x.{x^3} - x.{x^2} + x.1 + 1.{x^3} - 1.{x^2} + 1.1\\ = {x^5} - {x^4} + {x^2} + {x^4} - {x^3} + x + {x^3} - {x^2} + 1\\ = {x^5} + x + 1\end{array}$
Cho \(A = 5x\left( {4{x^2} - 2x + 1} \right) - 2x\left( {10{x^2} - 5x - 2} \right) - 9x + 1\). Chọn câu đúng.
-
A
\(A = 9x\)
-
B
\(A = 18x + 1\)
-
C
\(A = 9x + 1\)
-
D
Giá trị của biểu thức $A$ không phụ thuộc vào biến $x.$
Đáp án của giáo viên lời giải hay : D
Sử dụng quy tắc nhân đơn thức với đa thức rồi cộng trừ các hạng tử đồng dạng
\(\begin{array}{l}\,\,\,\,\,\,\,A = 5x\left( {4{x^2} - 2x + 1} \right) - 2x\left( {10{x^2} - 5x - 2} \right) - 9x + 1\\ \Leftrightarrow A = 5x.4{x^2} - 5x.2x + 5x.1 - 2x.10{x^2} - 2x.\left( { - 5x} \right) - 2x\left( { - 2} \right) - 9x + 1\\ \Leftrightarrow A = 20{x^3}-{\rm{ }}10{x^2} + {\rm{ }}5x{\rm{ }}-{\rm{ }}20{x^3} + {\rm{ }}10{x^2} + {\rm{ }}4x - 9x + 1\\ \Leftrightarrow A = 9x - 9x + 1\\ \Leftrightarrow A = 1\end{array}\)
Vậy giá trị của biểu thức $A$ không phụ thuộc vào biến $x.$
Tìm \(x\) biết \(\left( {x + 2} \right)(x + 3) - \left( {x - 2} \right)\left( {x + 5} \right) = 6\)
-
A
\(x = - 5.\)
-
B
\(x = 5.\)
-
C
\(x = - 10.\)
-
D
\(x = - 1.\)
Đáp án của giáo viên lời giải hay : A
Biến đổi vế trái bằng cách sử dụng quy tắc nhân đa thức với đa thức rồi cộng trừ các hạng tử đồng dạng
Từ đó tìm \(x.\)
\(\begin{array}{l}\left( {x + 2} \right)(x + 3) - \left( {x - 2} \right)\left( {x + 5} \right) = 6\\ \Leftrightarrow x.x + 3.x + 2.x + 2.3 - x.x - 5.x + 2.x + 2.5 = 6\\ \Leftrightarrow {x^2} + 3x + 2x + 6 - {x^2} - 5x + 2x + 10 = 6\\ \Leftrightarrow 2x + 16 = 6\\ \Leftrightarrow 2x = - 10\\ \Leftrightarrow x = - 5\end{array}\)
Vậy \(x = - 5.\)
Rút gọn biểu thức \({\left( {3x + 1} \right)^2} - 2\left( {3x + 1} \right)\left( {3x + 5} \right) + {\left( {3x + 5} \right)^2}\) ta được
-
A
\(8\)
-
B
\(16\)
-
C
\(24\)
-
D
$4$
Đáp án của giáo viên lời giải hay : B
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
\(\begin{array}{l}{\left( {3x + 1} \right)^2} - 2\left( {3x + 1} \right)\left( {3x + 5} \right) + {\left( {3x + 5} \right)^2}\\ = {\left( {\left( {3x + 1} \right) - \left( {3x + 5} \right)} \right)^2}\\ = {\left( {3x + 1 - 3x - 5} \right)^2}\\ = {( - 4)^2} = 16\end{array}\)
Cho biết \({\left( {x + 4} \right)^2} - \left( {x - 1} \right)\left( {x + 1} \right) = 16\). Hỏi giá trị của \(x\) là:
-
A
\(\dfrac{1}{8}\)
-
B
\(8\)
-
C
\( - \dfrac{1}{8}\)
-
D
$ - 8\left( {x + 5} \right)$
Đáp án của giáo viên lời giải hay : C
Sử dụng các hằng đẳng thức \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\); \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)
Sau đó cộng trừ các hạng tử đồng dạng để tìm \(x.\)
\(\begin{array}{l}{\left( {x + 4} \right)^2} - \left( {x - 1} \right)\left( {x + 1} \right) = 16\\ \Leftrightarrow {x^2} + 2.x.4 + {4^2} - \left( {{x^2} - 1} \right) = 16\\ \Leftrightarrow {x^2} + 8x + 16 - {x^2} + 1 = 16\\ \Leftrightarrow 8x = 16 - 16 - 1\\ \Leftrightarrow 8x = - 1\\ \Leftrightarrow x = - \dfrac{1}{8}\end{array}\)
Cho $x + y = 3$. Tính giá trị của biểu thức: $A = {x^2} + 2xy + {y^2} - 4x - 4y + 1$.
-
A
\(\dfrac{1}{2}\)
-
B
\(1\)
-
C
\(2\)
-
D
$ - 2$
Đáp án của giáo viên lời giải hay : D
Sử dụng hằng đẳng thức \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) và nhóm các hạng tử để biến đổi \(A\) sao cho xuất hiện hạng tử \(x + y.\)
\(A = {x^2} + 2xy + {y^2} - 4x - 4y + 1 \)\(= \left( {{x^2} + 2xy + {y^2}} \right) - \left( {4x + 4y} \right) + 1 \)\(= {\left( {x + y} \right)^2} - 4\left( {x + y} \right) + 1\)
Tại $x + y = 3$ , ta có: \(A = {3^2} - 4.3 + 1 = - 2\)
Tìm \(x\) biết: \({\left( {x + 1} \right)^3} - {\left( {x - 1} \right)^3} - 6{\left( {x - 1} \right)^2} = - 10\)
-
A
\(x = - \dfrac{1}{2}\)
-
B
\(x = 1\)
-
C
\(x = - 2\)
-
D
$x = 3$
Đáp án của giáo viên lời giải hay : A
Sử dụng các hằng đẳng thức\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\); \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\);\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Sau đó cộng trừ các hạng tử đồng dạng để tìm \(x.\)
\({\left( {x + 1} \right)^3} - {\left( {x - 1} \right)^3} - 6{\left( {x - 1} \right)^2} = - 10\)
\( \Leftrightarrow {x^3} + 3{x^2} + 3x + 1 - \left( {{x^3} - 3{x^2} + 3x - 1} \right) - 6\left( {{x^2} - 2x + 1} \right) = - 10\)
\(\Leftrightarrow {x^3} + 3{x^2} + 3x + 1 - {x^3} + 3{x^2} - 3x + 1 - 6{x^2} + 12x - 6 = - 10\)\(\Leftrightarrow12x - 4 = - 10\)
\(\Leftrightarrow 12x = - 10 + 4\)
\(\Leftrightarrow 12x = - 6\)
\( \Leftrightarrow x = \dfrac{{ - 1}}{2}\)
Kết quả phân tích đa thức \(6{x^2}y - 12x{y^2}\) là:
-
A
\(6xy\left( {x - 2y} \right)\)
-
B
\(6xy\left( {x - y} \right)\)
-
C
\(6xy\left( {x + 2y} \right)\)
-
D
\(6xy\left( {x + y} \right)\)
Đáp án của giáo viên lời giải hay : A
Sử dụng phương pháp đặt nhân tử chung
\(6{x^2}y - 12x{y^2} = 6xy.x - 6xy.2y = 6xy\left( {x - 2y} \right)\)
Điền đơn thức vào chỗ trống: \(12{x^3}{y^2}{z^2} - 18{x^2}{y^2}{z^4} = ....\left( {2x - 3{z^2}} \right)\)
-
A
$6x{y^2}{z^2}$
-
B
$6{x^2}{y^2}{z^2}$
-
C
$6{y^2}{z^2}$
-
D
$6{x^3}{y^2}{z^2}$
Đáp án của giáo viên lời giải hay : B
Sử dụng phương pháp đặt nhân tử chung
\(12{x^3}{y^2}{z^2} - 18{x^2}{y^2}{z^4} = 6{x^2}{y^2}{z^2}.2x - 6{x^2}{y^2}{z^2}.3{z^2} = 6{x^2}{y^2}{z^2}\left( {2x - 3{z^2}} \right)\)
Vậy đơn thức điền vào chỗ trống là: \(6{x^2}{y^2}{z^2}\)
Tìm \(x\) biết: $2x\left( {x - 3} \right) + 5\left( {x - 3} \right) = 0$
-
A
$x = \dfrac{5}{2}$ hoặc $x = 3$
-
B
$x = - \dfrac{5}{2}$ hoặc $x = 3$
-
C
$x = \dfrac{5}{2}$ hoặc $x = - 3$
-
D
$x = \dfrac{2}{5}$ hoặc $x = 3$
Đáp án của giáo viên lời giải hay : B
Sử dụng phương pháp đặt nhân tử chung đưa về phương trình tích \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\(\begin{array}{l}\;\;\;2x\left( {x - 3} \right) + 5\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {2x + 5} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x + 5 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{5}{2}\\x = 3\end{array} \right.\end{array}\)
Vậy \(x = - \dfrac{5}{2}\) hoặc $ x = 3$
Tính giá trị của biểu thức $A = x\left( {x - 2009} \right) - y\left( {2009 - x} \right)$ tại $x = 3009$ và $y = 1991$:
-
A
$5000000$
-
B
$500000$
-
C
$50000$
-
D
$5000$
Đáp án của giáo viên lời giải hay : A
Sử dụng phương pháp đặt nhân tử chung để thu gọn \(A.\) Sau đó thay $x = 3009$ và $y = 1991$ để tính toán.
\(\begin{array}{l}\;\;\;A = x\left( {x - 2009} \right) - y\left( {2009 - x} \right)\\ \Leftrightarrow A = x\left( {x - 2009} \right) + y\left( {x - 2009} \right)\\ \Leftrightarrow A = \left( {x + y} \right)\left( {x - 2009} \right)\end{array}\)
Với $x = 3009$ và $y = 1991$, giá trị của biểu thức là:
\(A = \left( {3009 + 1991} \right)\left( {3009 - 2009} \right) = 5000.1000 = 5000000\)
Chọn câu sai.
-
A
\(15{x^2} + 10xy = 5x\left( {3x + 2y} \right)\)
-
B
\(35x\left( {y - 8} \right) - 14y\left( {8 - y} \right) = 7\left( {5x + 2y} \right)\left( {y - 8} \right)\)
-
C
\( - x + 6{x^2}y - 12xy + 2 = \left( {6xy + 1} \right)\left( {x - 2} \right)\)
-
D
\({x^3} - {x^2} + x - 1 = \left( {{x^2} + 1} \right)\left( {x - 1} \right)\)
Đáp án của giáo viên lời giải hay : C
Sử dụng phương pháp đặt nhân tử chung và nhóm hạng tử thích hợp
Ta có
+) \(15{x^2} + 10xy = 5x.3x + 5x.2y = 5x\left( {3x + 2y} \right)\)
+) \(35x\left( {y - 8} \right) - 14y\left( {8 - y} \right) = 7.5x\left( {y - 8} \right) + 7.2y\left( {y - 8} \right) = \left( {7.5x + 7.2y} \right)\left( {y - 8} \right) = 7\left( {5x + 2y} \right)\left( {y - 8} \right)\)
+)
\(\begin{array}{l} - x + 6{x^2}y - 12xy + 2\\ = \left( {6{x^2}y - 12xy} \right) - \left( {x - 2} \right)\\ = \left( {6xy.x - 6xy.2} \right) - \left( {x - 2} \right)\\ = 6xy\left( {x - 2} \right) - \left( {x - 2} \right)\\ = \left( {6xy - 1} \right)\left( {x - 2} \right)\end{array}\)
+)
\(\begin{array}{l}\;{x^3} - {x^2} + x - 1\\ = {x^2}.x - {x^2} + x - 1\\ = {x^2}\left( {x - 1} \right) + \left( {x - 1} \right)\\ = \left( {{x^2} + 1} \right)\left( {x - 1} \right)\end{array}\)
Vậy A, B, D đúng, C sai.
Giá trị lớn nhất của \(x\) thỏa mãn phương trình \(\;7{x^2}\left( {x - 7} \right) + 5x\left( {7 - x} \right) = 0\) là
-
A
$x = \dfrac{5}{7}$
-
B
$x = 7$
-
C
$x = 0$
-
D
$x = 8$
Đáp án của giáo viên lời giải hay : B
+ Sử dụng phương pháp đặt nhân tử chung để đưa phương trình về dạng \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\(\begin{array}{l}7{x^2}\left( {x - 7} \right) + 5x\left( {7 - x} \right) = 0\\ \Leftrightarrow 7x.x\left( {x - 7} \right) - 5.x\left( {x - 7} \right) = 0\\ \Leftrightarrow \left( {7x.x - 5.x} \right)\left( {x - 7} \right) = 0\\ \Leftrightarrow x\left( {7x - 5} \right)\left( {x - 7} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\7x - 5 = 0\\x - 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{5}{7}\\x = 7\end{array} \right.\end{array}\)
Giá trị lớn nhất của \(x\) thỏa mãn đề bài là \(x = 7.\)
Đa thức \(12x - 9 - 4{x^2}\) được phân tích thành:
-
A
\(\left( {2x - 3} \right)\left( {2x + 3} \right)\)
-
B
\( - {\left( {2x - 3} \right)^2}\)
-
C
\({\left( {3 - 2x} \right)^2}\)
-
D
\( - {\left( {2x + 3} \right)^2}\)
Đáp án của giáo viên lời giải hay : B
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) để phân tích đa thức thành nhân tử
\(12x - 9 - 4{x^2} = - \left( {4{x^2} - 12x + 9} \right) = - \left( {{{\left( {2x} \right)}^2} - 2.2x.3 + {3^2}} \right) = - {\left( {2x - 3} \right)^2}\)
Phân tích đa thức \({x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}\) thành nhân tử:
-
A
\({\left( {x - y} \right)^3}\)
-
B
${\left( {2x - y} \right)^3}$
-
C
${x^3} - {\left( {2y} \right)^3}$
-
D
${\left( {x - 2y} \right)^3}$
Đáp án của giáo viên lời giải hay : D
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) để phân tích đa thức thành nhân tử
\({x^3} - 6{x^2}y + 12x{y^2} - 8{y^3} = {x^3} - 3.{x^2}.\left( {2y} \right) + 3.x.{\left( { 2y} \right)^2} - {\left( { 2y} \right)^3} = {\left( {x - 2y} \right)^3}\)
Phân tích đa thức thành nhân tử: \(5{x^2} + 10xy - 4x - 8y\)
-
A
\(\left( {5x - 2y} \right)\left( {x + 4y} \right)\)
-
B
\(\left( {5x + 4} \right)\left( {x - 2y} \right)\)
-
C
\(\left( {x + 2y} \right)\left( {5x - 4} \right)\)
-
D
\(\left( {5x - 4} \right)\left( {x - 2y} \right)\)
Đáp án của giáo viên lời giải hay : C
Nhóm hạng tử thứ 1 với hạng tử thứ 2 và nhóm hạng tử thứ 3 với hạng tử thứ 4 để xuất hiện nhân tử chung.
Đặt nhân tử chung để được tích của các đa thức.
\(\begin{array}{l}\,\,\,\,\,5{x^2} + 10xy - 4x - 8y = \left( {5{x^2} + 10xy} \right) - \left( {4x + 8y} \right)\\ = 5x\left( {x + 2y} \right) - 4\left( {x + 2y} \right) = \left( {5x - 4} \right)\left( {x + 2y} \right)\end{array}\)
Điền vào chỗ trống: \(3{x^2} + 6x{y^2} - 3{y^2} + 6{x^2}y = 3\left( {...} \right)\left( {x + y} \right)\)
-
A
\(\left( {x + y + 2xy} \right)\)
-
B
\(\left( {x - y + 2xy} \right)\)
-
C
\(\left( {x - y + xy} \right)\)
-
D
\(\left( {x - y + 3xy} \right)\)
Đáp án của giáo viên lời giải hay : B
- Sử dụng phương pháp giao hoán, kết hợp để sắp xếp các hạng tử.
- Nhóm hạng tử thứ 1 với hạng tử thứ 3 và nhóm hạng tử thứ 2 với hạng tử thứ 4 để xuất hiện nhân tử chung.
- Đặt nhân tử chung để được tích của các đa thức.
- So sánh với đề bài để tìm ra đa thức cần điền vào chỗ trống.
\(\begin{array}{l}\,\,\,\,\,3{x^2} + 6x{y^2} - 3{y^2} + 6{x^2}y = \left( {3{x^2} - 3{y^2}} \right) + \left( {6x{y^2} + 6{x^2}y} \right)\\ = 3\left( {{x^2} - {y^2}} \right) + 6xy\left( {y + x} \right) = 3\left( {x - y} \right)\left( {x + y} \right) + 6xy\left( {x + y} \right)\\ = \left[ {3\left( {x - y} \right) + 6xy} \right]\left( {x + y} \right) = 3\left( {x - y + 2xy} \right)\left( {x + y} \right).\end{array}\)
Vậy chỗ trống là \(\left( {x - y + 2xy} \right)\).
Phân tích đa thức \(m.{n^3} - 1 + m - {n^3}\) thành nhân tử, ta được:
-
A
\(\left( {m - 1} \right)\left( {n + 1} \right)\left( {{n^2} - n + 1} \right)\)
-
B
\({n^2}\left( {n + 1} \right)\left( {m - 1} \right)\)
-
C
\(\left( {m + 1} \right)\left( {{n^2} + 1} \right)\)
-
D
\(\left( {{n^3} - 1} \right)\left( {m - 1} \right)\)
Đáp án của giáo viên lời giải hay : A
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
- Đặt nhân tử chung để được tích các đa thức.
\(\begin{array}{l}\,\,\,\,\,m.{n^3} - 1 + m - {n^3}\\ = \left( {m{n^3} - {n^3}} \right) + \left( {m - 1} \right)\\ = {n^3}\left( {m - 1} \right) + \left( {m - 1} \right)\\ = \left( {{n^3} + 1} \right)\left( {m - 1} \right)\\ = \left( {n + 1} \right)\left( {{n^2} - n + 1} \right)\left( {m - 1} \right).\end{array}\)
Điền vào chỗ trống \(4{x^2} + 4x - {y^2} + 1 = \left( {...} \right)\left( {2x + y + 1} \right)\):
-
A
\(2x + y + 1\)
-
B
\(2x - y + 1\)
-
C
\(2x - y\)
-
D
\(2x + y\)
Đáp án của giáo viên lời giải hay : B
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp để xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
- Đặt nhân tử chung để được tích các đa thức.
- So sánh với yêu cầu của đề bài để chọn đáp án đúng.
\(\begin{array}{l}\,\,\,\,\,4{x^2} + 4x - {y^2} + 1\\ = \left( {{{\left( {2x} \right)}^2} + 2.2x + 1} \right) - {y^2}\\ = {\left( {2x + 1} \right)^2} - {y^2}\\ = \left( {2x + 1 - y} \right)\left( {2x + 1 + y} \right)\\ = \left( {2x - y + 1} \right)\left( {2x + y + 1} \right).\end{array}\)
Vậy đa thức trong chỗ trống là \(2x - y + 1\).
Chọn câu đúng.
-
A
\({x^4} - 4{x^3} + 4{x^2} = {x^2}{\left( {x + 2} \right)^2}\)
-
B
\({x^4} - 4{x^3} + 4{x^2} = {x^2}{\left( {x - 2} \right)^2}\)
-
C
\({x^4} - 4{x^3} + 4{x^2} = {x^2}\left( {x - 2} \right)\)
-
D
\({x^4} - 4{x^3} + 4{x^2} = x{\left( {x - 2} \right)^2}\)
Đáp án của giáo viên lời giải hay : B
Đặt nhân tử chung, dùng hằng đẳng thức để phân tích
\(\begin{array}{l}{x^4} - 4{x^3} + 4{x^2}\\ = {x^2}\left( {{x^2} - 4x + 4} \right)\\ = {x^2}\left( {{x^2} - 2.2.x + {2^2}} \right)\\ = {x^2}{\left( {x - 2} \right)^2}.\end{array}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn \({x^3} - 3{x^2} + 3 - x = 0\)
-
A
$1$
-
B
$2$
-
C
$3$
-
D
$4$
Đáp án của giáo viên lời giải hay : C
+ Sử dụng phương pháp nhóm hạng tử và đặt nhân tử chung để đưa phương trình về dạng \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\(\begin{array}{l}{x^3} - 3{x^2} + 3 - x = 0\\ \Leftrightarrow {x^2}.x - 3.{x^2} + \left( {3 - x} \right) = 0\\ \Leftrightarrow {x^2}\left( {x - 3} \right) - \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\\x = 3\end{array} \right.\end{array}\)
Vậy $x = 1$ hoặc $x = 3$ hoặc \(x = - 1\).
Vậy có ba giá trị của \(x\) thỏa mãn đề bài.
Cho \(4{x^2} - 25 - \left( {2x + 7} \right)\left( {5 - 2x} \right) = \left( {2x - 5} \right)\left( {...} \right)\) . Biểu thức điền vào dấu ba chấm là
-
A
\(2x + 12\)
-
B
$4x - 12$
-
C
$x + 3$
-
D
$4x + 12$
Đáp án của giáo viên lời giải hay : D
Sử dụng hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) và phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử
\(\begin{array}{l}\;4{x^2} - 25 - \left( {2x + 7} \right)\left( {5 - 2x} \right)\\ = {\left( {2x} \right)^2} - {5^2} - \left( {2x + 7} \right)\left( {5 - 2x} \right)\\ = \left( {2x - 5} \right)\left( {2x + 5} \right) - \left( {2x + 7} \right)\left( {5 - 2x} \right)\\ = \left( {2x - 5} \right)\left( {2x + 5} \right) + \left( {2x + 7} \right)\left( {2x - 5} \right)\\ = \left( {2x - 5} \right)\left( {2x + 5 + 2x + 7} \right) = \left( {2x - 5} \right)\left( {4x + 12} \right)\end{array}\)
Biểu thức cần điền là \(4x + 12.\)
Chọn câu sai.
-
A
${x^2} + 4x - {y^2} + 4 = \left( {x - y + 2} \right)\left( {x + y + 2} \right)$
-
B
\({\left( {2{x^2} - y} \right)^2} - 64{y^2} = \left( {2{x^2} - 9y} \right)\left( {2{x^2} + 7y} \right)\)
-
C
\( - {x^3} + 6{x^2}y - 12x{y^2} + 8{y^3} = {\left( {2y - x} \right)^3}\)
-
D
\(\;{x^8} - {y^8} = {\left( {{x^4}} \right)^2} - {\left( {{y^4}} \right)^2} = \left( {{x^4} + {y^4}} \right)\left( {{x^2} + {y^2}} \right)\left( {x + y} \right)\)
Đáp án của giáo viên lời giải hay : D
Sử dụng các phương pháp đặt nhân tử chung, dùng hằng đẳng thức, thêm bớt hạng tử .. và phối hợp nhiều phương pháp để phân tích.
\( + )\;{x^2} + 4x - {y^2} + 4 = \left( {{x^2} + 4x + 4} \right) - {y^2} = \left( {{x^2} + 2.2.x + {2^2}} \right) - {y^2} = {\left( {x + 2} \right)^2} - {y^2} = \left( {x - y + 2} \right)\left( {x + y + 2} \right)\)
\( + )\;{\left( {2{x^2} - y} \right)^2} - 64{y^2} = {\left( {2{x^2} - y} \right)^2} - {\left( {8y} \right)^2} = \left( {2{x^2} - y - 8y} \right)\left( {2{x^2} - y + 8y} \right) = \left( {2{x^2} - 9y} \right)\left( {2{x^2} + 7y} \right)\)
\( + )\; - {x^3} + 6{x^2}y - 12x{y^2} + 8{y^3} = {\left( { - x} \right)^3} + 3.{x^2}.2y + 3.\left( { - x} \right).{\left( {2y} \right)^2} + {\left( {2y} \right)^3} = {\left( { - x + 2y} \right)^3} = {\left( {2y - x} \right)^3}\)
\( + )\;{x^8} - {y^8} = {\left( {{x^4}} \right)^2} - {\left( {{y^4}} \right)^2} = \left( {{x^4} + {y^4}} \right)\left( {{x^4} - {y^4}} \right)\)
\( = \left( {{x^4} + {y^4}} \right)\left( {{x^2} + {y^2}} \right)\left( {{x^2} - {y^2}} \right) = \left( {{x^4} + {y^4}} \right)\left( {{x^2} + {y^2}} \right)\left( {x + y} \right)\left( {x - y} \right)\)
Nên A, B, C đúng. D sai.
Có bao nhiêu giá trị của \(x\) thỏa mãn \({\left( {x + 5} \right)^2} - 2\left( {x + 5} \right)\left( {x - 2} \right) + {\left( {x - 2} \right)^2} = 49\)
-
A
$1$
-
B
$2$
-
C
$3$
-
D
Vô số
Đáp án của giáo viên lời giải hay : D
Sử dụng hằng đẳng thức để biến đổi vế trái từ đó đưa về dạng \({A^2} = {m^2}\)
$\begin{array}{l}{\left( {x + 5} \right)^2} - 2\left( {x + 5} \right)\left( {x - 2} \right) + {\left( {x - 2} \right)^2} = 49\\ \Leftrightarrow {\left( {\left( {x + 5} \right) - \left( {x - 2} \right)} \right)^2} = 49\\ \Leftrightarrow {\left( {x + 5 - x + 2} \right)^2} = 49\\ \Leftrightarrow {7^2} = 49\end{array}$
Vậy với mọi \(x\) đều thỏa mãn.
Rút gọn biểu thức \(B = (x - 2)\left( {{x^2} + 2x + 4} \right) - x\left( {x - 1} \right)\left( {x + 1} \right) + 3x\)
-
A
$x-8$
-
B
$8-4x$
-
C
$8-x$
-
D
\(4x - 8\)
Đáp án của giáo viên lời giải hay : D
Sử dụng hằng đẳng thức \({A^3} + {B^3} = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)\) và \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) để biến đổi và rút gọn \(B.\)
\(\begin{array}{l}B = \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) - x\left( {x - 1} \right)\left( {x + 1} \right) + 3x\\B = \left( {x - 2} \right)\left( {{x^2} + x.2 + {2^2}} \right) - x\left( {{x^2} - 1} \right) + 3x\\B = {x^3} - {2^3} - x.{x^2} + x.1 + 3x\\B = {x^3} - 8 - {x^3} + x + 3x\\B = 4x - 8\end{array}\)
Tìm giá trị của $x$ thỏa mãn \(x\left( {2x - 7} \right) - 4x + 14 = 0\)
-
A
\(x = \dfrac{7}{2}\) hoặc \(x = - 2\)
-
B
\(x = \dfrac{{ - 7}}{2}\) hoặc \(x = 2\)
-
C
\(x = \dfrac{7}{2}\) hoặc \(x = 2\)
-
D
\(x = \dfrac{{ - 7}}{2}\) hoặc \(x = - 2\)
Đáp án của giáo viên lời giải hay : C
Nhóm hạng tử để xuất hiện nhân tử chung.
Đặt nhân tử chung để được tích của các đa thức.
Để tích các đa thức bằng 0 thì giá trị từng đa thức phải bằng 0.
Suy ra giá trị x cần tìm.
\(\begin{array}{l}\,\,\,\,\,\,\,\,x\left( {2x - 7} \right) - 4x + 14 = 0\\ \Leftrightarrow x\left( {2x - 7} \right) - 2\left( {2x - 7} \right) = 0\\ \Leftrightarrow \left( {2x - 7} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {2x - 7} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - 7 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{7}{2}\\x = 2\end{array} \right..\end{array}\)
Vậy \(x = \dfrac{7}{2}\) hoặc \(x = 2\).
Chọn câu đúng nhất:
-
A
\({x^2} - 2x - 4{y^2} - 4y = \left( {x - 2y - 2} \right)\left( {x + 2y} \right)\)
-
B
\({x^2} + {y^2}x + {x^2}y + xy - x - y = \left( {x + xy - 1} \right)\left( {x + y} \right)\)
-
C
Cả A, B đều đúng
-
D
Cả A, B đều sai
Đáp án của giáo viên lời giải hay : C
Sử dụng phương pháp phân phối phép nhân và phép trừ, giao hoán, kết hợp để sắp xếp và tạo ra các hạng tử cần thiết.
Sau đó, nhóm hạng tử để xuất hiện nhân tử chung.
Đặt nhân tử chung để được tích của các đa thức.
\(\begin{array}{l} + ){x^2} - 2x - 4{y^2} - 4y\\ = \left( {{x^2} - 4{y^2}} \right) - \left( {2x + 4y} \right)\\ = \left( {x - 2y} \right)\left( {x + 2y} \right) - 2\left( {x + 2y} \right)\\ = \left( {x - 2y - 2} \right)\left( {x + 2y} \right).\end{array}\)
\(\begin{array}{l} + )\;{x^2} + {y^2}x + {x^2}y + xy - x - y\\ = \left( {{x^2} + xy} \right) + \left( {{y^2}x + {x^2}y} \right) - \left( {x + y} \right)\\ = x\left( {x + y} \right) + xy\left( {y + x} \right) - \left( {x + y} \right)\\ = \left( {x + xy - 1} \right)\left( {x + y} \right)\end{array}\)
Vậy A, B đều đúng.
Tổng các giá trị của \(x\) thỏa mãn \(x\left( {x - 1} \right)\left( {x + 1} \right) + {x^2} - 1 = 0\) là
-
A
\(2\)
-
B
\( - 1\)
-
C
\(1\)
-
D
\(0\)
Đáp án của giáo viên lời giải hay : D
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
- Từ đó đưa về dạng \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\(\begin{array}{l}x(x - 1)\left( {x + 1} \right) + {x^2} - 1 = 0\\ \Leftrightarrow x\left( {x - 1} \right)\left( {x + 1} \right) + \left( {{x^2} - 1} \right) = 0\\ \Leftrightarrow x\left( {x - 1} \right)\left( {x + 1} \right) + \left( {x - 1} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 1} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2}\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right.\end{array}\)
Vậy \(x = - 1\) hoặc \(x = 1\).
Tổng các giá trị của \(x\) là \(1 + \left( { - 1} \right) = 0.\)
Tính giá trị của biểu thức \(B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\) khi \({x^3} - x = 6\):
-
A
$36$
-
B
$42$
-
C
$48$
-
D
$56$
Đáp án của giáo viên lời giải hay : B
+ Sử dụng phương pháp giao hoán, kết hợp và tách hạng tử (tách hạng tử thứ 2 thành 2 hạng tử giống nhau) để sắp xếp và tạo ra các hạng tử cần thiết.
+ Sau khi tách hạng tử, nhóm các hạng tử thích hợp để xuất hiện nhân tử chung giống với \({x^3} - x\).
+ Đặt nhân tử chung để được tích của các đa thức.
+ Sau đó thế biểu thức \({x^3} - x = 6\) vào biểu thức vừa biến đổi để tính giá trị biểu thức.
\(\begin{array}{l}\,\,\,\,\,\,\,\,B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\\ \Leftrightarrow B = {x^6} - {x^4} - {x^4} + {x^3} + {x^2} - x\\ \Leftrightarrow B = \left( {{x^6} - {x^4}} \right) - \left( {{x^4} - {x^2}} \right) + \left( {{x^3} - x} \right)\\ \Leftrightarrow B = {x^3}\left( {{x^3} - x} \right) - x\left( {{x^3} - x} \right) + \left( {{x^3} - x} \right)\\ \Leftrightarrow B = \left( {{x^3} - x + 1} \right)\left( {{x^3} - x} \right)\end{array}\)
Tại \({x^3} - x = 6\), ta có: \(B = \left( {6 + 1} \right).6 = 7.6 = 42\)
Phân tích đa thức \(\;2{x^3}y - 2x{y^3} - 4x{y^2} - 2xy\) thành nhân tử ta được
-
A
\(2xy\left( {x - y - 1} \right)\left( {x + y + 1} \right)\)
-
B
\(2xy\left( {x - y - 1} \right)\left( {x + y - 1} \right)\)
-
C
\(xy\left( {x - y - 1} \right)\left( {x + y + 1} \right)\)
-
D
\(2xy\left( {x - y - 1} \right)\left( {x - y + 1} \right)\)
Đáp án của giáo viên lời giải hay : A
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới. Từ đó biến đổi tiếp để được tích các đa thức.
\(\begin{array}{l}2{x^3}y - 2x{y^3} - 4x{y^2} - 2xy\\ = 2xy\left( {{x^2} - {y^2} - 2y - 1} \right)\\ = 2xy\left[ {{x^2} - \left( {{y^2} + 2y + 1} \right)} \right]\\ = 2xy\left[ {{x^2} - {{\left( {y + 1} \right)}^2}} \right]\\ = 2xy\left( {x - y - 1} \right)\left( {x + y + 1} \right).\end{array}\)
Chọn câu sai:
-
A
\(16{x^4}\left( {x - y} \right) - x + y = \left( {2x - 1} \right)\left( {2x + 1} \right)\left( {4{x^2} + 1} \right)\left( {x - y} \right)\)
-
B
\(16{x^3} - 54{y^3} = 2\left( {2x - 3y} \right)\left( {4{x^2} + 6xy + 9{y^2}} \right)\)
-
C
\(16{x^3} - 54{y^3} = 2\left( {2x - 3y} \right){\left( {2x + 3y} \right)^2}\)
-
D
\(16{x^4}\left( {x - y} \right) - x + y = \left( {4{x^2} - 1} \right)\left( {4{x^2} + 1} \right)\left( {x - y} \right)\)
Đáp án của giáo viên lời giải hay : C
Dùng các hằng đẳng thức đáng nhớ, đặt nhân tử chung và nhóm hạng tử để phân tích
\(\begin{array}{l} + )\,16{x^4}\left( {x - y} \right) - x + y\\ = 16{x^4}\left( {x - y} \right) - \left( {x - y} \right)\\ = \left( {16{x^4} - 1} \right)\left( {x - y} \right)\\ = \left[ {{{\left( {2x} \right)}^4} - 1} \right]\left( {x - y} \right)\\ = \left[ {{{\left( {2x} \right)}^2} - 1} \right]\left[ {\left( {2{x^2}} \right) + 1} \right]\left( {x - y} \right)\\ = \left( {2x - 1} \right)\left( {2x + 1} \right)\left( {4{x^2} + 1} \right)\left( {x - y} \right).\end{array}\)
\(\begin{array}{l} + )\;16{x^3} - 54{y^3}\\ = 2\left( {8{x^3} - 27{y^3}} \right)\\ = 2\left[ {{{\left( {2x} \right)}^3} - {{\left( {3y} \right)}^3}} \right]\\ = 2\left( {2x - 3y} \right)\left[ {{{\left( {2x} \right)}^2} + 2x.3y + {{\left( {3y} \right)}^2}} \right]\\ = 2\left( {2x - 3y} \right)\left( {4{x^2} + 6xy + 9{y^2}} \right).\end{array}\)
Vậy A, B, D đúng. C sai
Tìm $x$ biết \({\left( {2x - 3} \right)^2} - 4{x^2} + 9 = 0\)
-
A
\(x = \dfrac{1}{2}\)
-
B
\(x = - \dfrac{3}{2}\)
-
C
\(x = \dfrac{3}{2}\)
-
D
\(x = \dfrac{2}{3}\)
Đáp án của giáo viên lời giải hay : C
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp để xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
- Đặt nhân tử chung để được dạng $A.B.C = 0$
- Suy ra $A = 0 $ hoặc $B = 0$ hoặc $C = 0.$
- Suy ra các giá trị của $x$ cần tìm.
\(\begin{array}{l}{\left( {2x - 3} \right)^2} - 4{x^2} + 9 = 0\\ \Leftrightarrow {\left( {2x - 3} \right)^2} - \left( {4{x^2} - 9} \right) = 0\\ \Leftrightarrow {\left( {2x - 3} \right)^2} - \left( {{{\left( {2x} \right)}^2} - {3^2}} \right) = 0\\ \Leftrightarrow {\left( {2x - 3} \right)^2} - \left( {2x - 3} \right)\left( {2x + 3} \right) = 0\\ \Leftrightarrow \left( {2x - 3} \right)\left( {2x - 3 - 2x - 3} \right) = 0\\ \Leftrightarrow \left( {2x - 3} \right)\left( { - 6} \right) = 0\\ \Leftrightarrow 2x - 3 = 0\\ \Leftrightarrow x = \dfrac{3}{2}\end{array}\)
Vậy \(x = \dfrac{3}{2}\).
Tìm $x$ biết \({x^3} - {x^2} - x + 1 = 0\)
-
A
\(x = 1\) hoặc \(x = - 1\)
-
B
\(x = - 1\) hoặc \(x = 0\)
-
C
\(x = 1\) hoặc \(x = 0\)
-
D
\(x = 1\)
Đáp án của giáo viên lời giải hay : A
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp để xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
- Đặt nhân tử chung để được dạng $A.B.C = 0$
- Suy ra $A = 0$ hoặc $B = 0$ hoặc $C = 0.$
- Suy ra các giá trị của $x$ cần tìm.
\(\begin{array}{l}\,\,\,\,\,\,\,{x^3} - {x^2} - x + 1 = 0\\ \Leftrightarrow \left( {{x^3} - {x^2}} \right) - \left( {x - 1} \right) = 0\\ \Leftrightarrow {x^2}\left( {x - 1} \right) - \left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 1} \right)\left( {x - 1} \right) = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\end{array}\)
Vậy \(x = 1\) hoặc \(x = - 1\).
Phân tích đa thức sau thành nhân tử: \({x^3} - 5x + 4\) ta được
-
A
\(\left( {x + 1} \right)\left( {{x^2} + x - 4} \right)\)
-
B
\(\left( {x - 1} \right)\left( {{x^2} - x - 4} \right)\)
-
C
\(\left( {x - 1} \right)\left( {{x^2} + x - 4} \right)\)
-
D
\(\left( {x - 1} \right)\left( {{x^2} + x + 4} \right)\)
Đáp án của giáo viên lời giải hay : C
- Tách 1 hạng tử thành nhiều hạng tử hoặc thêm, bớt cùng một hạng tử làm xuất hiện nhân tử chung hoặc các hằng đẳng thức.
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
\(\begin{array}{l}\,\,\,\,\,{x^3} - 5x + 4\\ = {x^3} - x - 4x + 4\\ = x\left( {{x^2} - 1} \right) - 4\left( {x - 1} \right)\\ = x\left( {x - 1} \right)\left( {x + 1} \right) - 4\left( {x - 1} \right)\\ = \left( {x - 1} \right)\left[ {x\left( {x + 1} \right) - 4} \right]\\ = \left( {x - 1} \right)\left( {{x^2} + x - 4} \right).\end{array}\)
Thực hiện phép tính: \(\left( {4{x^4} - 4{x^3} + 3x - 3} \right):\left( {x - 1} \right)\)
-
A
$4{x^2} + 3$
-
B
$4{x^3} - 3$
-
C
$4{x^2} - 3$
-
D
$4{x^3} + 3$
Đáp án của giáo viên lời giải hay : D
- Đặt phép chia, thực hiện phép tính (Hoặc biến đổi số bị chia thành tích các đa thức trong đó có 1 đa thức giống số chia, sau đó thực hiện phép tính).
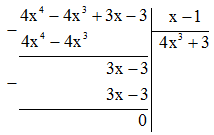
$\left( {4{x^4} - 4{x^3} + 3x - 3} \right):\left( {x - 1} \right) = 4{x^3} + 3$
Rút gọn biểu thức: $A = \dfrac{{4{x^3} - 5{x^2} + 1}}{{{x} - 1}}$
-
A
\(4{x^2} - x - 1\)
-
B
\(4{x^2} + x - 1\)
-
C
\(4{x^2} + x + 1\)
-
D
\(4{x^2} - x + 1\)
Đáp án của giáo viên lời giải hay : A
- Kết hợp các phương pháp phân tích đa thức thành nhân tử và thực hiện phép tính chia để thu được biểu thức rút gọn.
$\begin{array}{l}A = \dfrac{{4{x^3} - 5{x^2} + 1}}{{x - 1}}\\\,\,\,\,\,\, = \dfrac{{4{x^3} - 4{x^2} - {x^2} + 1}}{{x - 1}}\\\,\,\,\,\,\, = \dfrac{{4{x^2}\left( {x - 1} \right) - \left( {{x^2} - 1} \right)}}{{x - 1}}\\\,\,\,\,\,\, = \dfrac{{4{x^2}\left( {x - 1} \right) - \left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\\,\,\,\,\,\, = \dfrac{{\left( {x - 1} \right)\left( {4{x^2} - x - 1} \right)}}{{x - 1}} = 4{x^2} - x - 1.\end{array}$
Thực hiện phép tính \(A = \left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right)\) ta được
-
A
\(3x - 1\)
-
B
\(3x + 1\)
-
C
\(3x\)
-
D
\(3\)
Đáp án của giáo viên lời giải hay : A
Đặt tính theo hàng dọc rồi thực hiện phép chia để tìm thương
\(\left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right)\)

\(\left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right) = 3x - 1.\)
Phân tích đa thức thành nhân tử ta được \({x^3} + 7{x^2} + 12x + 4 = \left( {x + 2} \right)\left( {{x^2} + a.x + 2} \right)\) . Khi đó giá trị của \(a\) là:
-
A
\(5\)
-
B
\( - 6\)
-
C
\( - 5\)
-
D
\(6\)
Đáp án của giáo viên lời giải hay : A
- Tách 1 hạng tử thành nhiều hạng tử hoặc thêm, bớt cùng một hạng tử làm xuất hiện nhân tử chung hoặc các hằng đẳng thức.
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
\(\begin{array}{l} + )\;{x^3} + 7{x^2} + 12x + 4\\ = {x^3} + 6{x^2} + {x^2} + 12x + 8 - 4\\ = \left( {{x^3} + 6{x^2} + 12x + 8} \right) + \left( {{x^2} - 4} \right)\\ = \left( {{x^3} + 3.2.{x^2} + {{3.2}^2}.x + {2^3}} \right) + \left( {{x^2} - 4} \right)\\ = {\left( {x + 2} \right)^3} + \left( {x - 2} \right)\left( {x + 2} \right)\\ = \left( {x + 2} \right)\left( {{{\left( {x + 2} \right)}^2} + x - 2} \right)\\ = \left( {x + 2} \right)\left( {{x^2} + 4x + 4 + x - 2} \right)\\ = \left( {x + 2} \right)\left( {{x^2} + 5x + 2} \right)\end{array}\)
Có bao nhiêu giá trị của $x$ thỏa mãn \(\,2{x^3}\left( {2x - 3} \right) - {x^2}\left( {4{x^2} - 6x + 2} \right) = 0\)
-
A
\(2\)
-
B
\(3\)
-
C
\(0\)
-
D
\(1\)
Đáp án của giáo viên lời giải hay : D
-Nhân đơn thức với đa thức rồi cộng trừ các hạng tử đồng dạng để biến đổi biểu thức thành tích các đa thức và đơn thức có dạng: $A.B = 0,$ suy ra $A = 0$ hoặc $B = 0,$ từ đó rút ra giá trị của $x$ cần tìm.
\(\begin{array}{l}2{x^3}\left( {2x - 3} \right) - {x^2}\left( {4{x^2} - 6x + 2} \right) = 0\\ \Leftrightarrow 4{x^4} - 6{x^3} - 4{x^4} + 6{x^3} - 2{x^2} = 0\\ \Leftrightarrow - 2{x^2} = 0\\ \Leftrightarrow x = 0\end{array}\)
Vậy $x = 0.$
Có \(1\) giá trị của \(x\) thỏa mãn đề bài.
Giá trị nhỏ nhất của biểu thức \(A = {x^2} - x + 1\) là:
-
A
\(\dfrac{2}{4}\)
-
B
\(\dfrac{3}{4}\)
-
C
\(1\)
-
D
\( - \dfrac{3}{4}\)
Đáp án của giáo viên lời giải hay : B
Biến đổi đưa về dạng \({\left( {x - a} \right)^2} + m\) rồi đánh giá \({\left( {x - a} \right)^2} + m \ge m\)
Giá trị nhỏ nhất của \({\left( {x - a} \right)^2} + m\) là \(m \Leftrightarrow x = a.\)
\(\begin{array}{l}A = {x^2} - x + 1 = {x^2} - 2.x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} + \dfrac{3}{4} = {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4}\\ \Rightarrow \;Min\;A = \dfrac{3}{4}\;\end{array}\)
Dấu “=” xảy ra khi \({\left( {x - \dfrac{1}{2}} \right)^2} = 0\) hay \(x = \dfrac{1}{2}\).
Giá trị lớn nhất của biểu thức \(B = - 9{x^2} + 2x - \dfrac{2}{9}\) là:
-
A
\(\dfrac{2}{9}\)
-
B
\( - \dfrac{2}{9}\)
-
C
\(\dfrac{1}{9}\)
-
D
\( - \dfrac{1}{9}\)
Đáp án của giáo viên lời giải hay : D
Biến đổi đưa về dạng \( - {\left( {x - a} \right)^2} + m\) rồi đánh giá \( - {\left( {x - a} \right)^2} + m \le m\)
Giá trị lớ nhất của \( - {\left( {x - a} \right)^2} + m\) là \(m \Leftrightarrow x = a.\)
\(B = - 9{x^2} + 2x - \dfrac{2}{9} \)\(= - {\left( {3x} \right)^2} + 2.3x.\dfrac{1}{3} - {\left( {\dfrac{1}{3}} \right)^2} - \dfrac{1}{9} \)\(= - \left( {{{\left( {3x} \right)}^2} - 2.3x.\dfrac{1}{3} + {{\left( {\dfrac{1}{3}} \right)}^2}} \right) - \dfrac{1}{9} \)\(= - {\left( {3x - \dfrac{1}{3}} \right)^2} - \dfrac{1}{9} \le - \dfrac{1}{9}\)
\( \Rightarrow \;Max\;B = - \dfrac{1}{9}\).
Dấu “=” xảy ra khi \({\left( {3x - \dfrac{1}{3}} \right)^2} = 0\) hay \(x = \dfrac{1}{9}\).
Tính giá trị biểu thức \(P = \left( { - 4{x^3}{y^3} + {x^3}{y^4}} \right):2x{y^2} - xy\left( {2x - xy} \right)\) cho \(x = 1,y = \dfrac{{ - 1}}{2}\);
-
A
\(P = - \dfrac{{19}}{8}\)
-
B
\(P = \dfrac{{19}}{8}\)
-
C
\(P = \dfrac{8}{{19}}\)
-
D
\(P = \dfrac{9}{8}\)
Đáp án của giáo viên lời giải hay : B
- Rút gọn biểu thức đã cho, sau đó thay giá trị của biến vào biểu thức rút gọn để tìm ra giá trị của biểu thức.
\(\begin{array}{l}\,\,\,\,\,\,\,\,P = \left( { - 4{x^3}{y^3} + {x^3}{y^4}} \right):2x{y^2} - xy\left( {2x - xy} \right)\\ \Leftrightarrow P = \left( { - 4{x^3}{y^3}} \right):2x{y^2} + {x^3}{y^4}:2x{y^2} - xy.2x + xy.xy\\ \Leftrightarrow P = - 2{x^2}y + \dfrac{1}{2}{x^2}{y^2} - 2{x^2}y + {x^2}{y^2}\\ \Leftrightarrow P = \dfrac{3}{2}{x^2}{y^2} - 4{x^2}y\\ \Leftrightarrow P = {x^2}y\left( {\dfrac{3}{2}y - 4} \right)\end{array}\)
Tại \(x = 1,y = \dfrac{{ - 1}}{2}\), ta có: \(P = {1^2}.\left( {\dfrac{{ - 1}}{2}} \right)\left( {\dfrac{3}{2}\left( {\dfrac{{ - 1}}{2}} \right) - 4} \right) = \left( {\dfrac{{ - 1}}{2}} \right)\left( {\dfrac{{ - 3}}{4} - 4} \right) = \left( {\dfrac{{ - 1}}{2}} \right)\left( {\dfrac{{ - 19}}{4}} \right) = \dfrac{{19}}{8}\)
Phân tích đa thức \({x^8} + {x^4} + 1\) thành nhân tử ta được
-
A
\(\left( {{x^4} - {x^2} + 1} \right)\left( {{x^2} - x + 1} \right)\left( {{x^2} - x - 1} \right)\)
-
B
\(\left( {{x^4} - {x^2} + 1} \right)\left( {{x^2} - x + 1} \right)\)
-
C
\(\left( {{x^4} - {x^2} + 1} \right)\left( {{x^2} - x + 1} \right)\left( {{x^2} + x + 1} \right)\)
-
D
\(\left( {{x^4} + {x^2} + 1} \right)\left( {{x^2} - x + 1} \right)\left( {{x^2} + x + 1} \right)\)
Đáp án của giáo viên lời giải hay : C
- Tách 1 hạng tử thành nhiều hạng tử hoặc thêm, bớt cùng một hạng tử làm xuất hiện nhân tử chung hoặc các hằng đẳng thức.
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
- Đặt nhân tử chung để được tích các đa thức.
\(\begin{array}{l}{x^8} + {x^4} + 1\\ = {x^8} + 2{x^4} + 1 - {x^4}\\ = \left( {{x^8} + 2{x^4} + 1} \right) - {x^4}\\ = \left[ {{{\left( {{x^4}} \right)}^2} + 2.{x^4}.1 + {1^2}} \right] - {x^4}\\ = {\left( {{x^4} + 1} \right)^2} - {\left( {{x^2}} \right)^2}\\ = \left( {{x^4} + 1 - {x^2}} \right)\left( {{x^4} + 1 + {x^2}} \right)\\ = \left( {{x^4} - {x^2} + 1} \right)\left( {{x^4} + 2{x^2} - {x^2} + 1} \right)\end{array}\)
\(\begin{array}{l} = \left( {{x^4} - {x^2} + 1} \right)\left[ {\left( {{{\left( {{x^2}} \right)}^2} + 2.1.{x^2} + 1} \right) - {x^2}} \right]\\ = \left( {{x^4} - {x^2} + 1} \right)\left[ {{{\left( {{x^2} + 1} \right)}^2} - {x^2}} \right]\\ = \left( {{x^4} - {x^2} + 1} \right)\left( {{x^2} + 1 - x} \right)\left( {{x^2} + 1 + x} \right)\\ = \left( {{x^4} - {x^2} + 1} \right)\left( {{x^2} - x + 1} \right)\left( {{x^2} + x + 1} \right).\end{array}\)
Cho \(S = 1 + x + {x^2} + {x^3} + {x^4} + {x^5}\), chọn câu đúng
-
A
\(xS - S = {x^6} - 1\)
-
B
\(xS - S = {x^6}\)
-
C
\(xS - S = {x^6} + 1\)
-
D
\(xS - S = {x^7} - 1\)
Đáp án của giáo viên lời giải hay : A
Thực hiện phép nhân đơn thức với đa thức để tìm ra đáp án đúng.
\(xS = x.(1 + x + {x^2} + {x^3} + {x^4} + {x^5}) = x + {x^2} + {x^3} + {x^4} + {x^5} + {x^6}.\)
\( \Rightarrow xS - S = x + {x^2} + {x^3} + {x^4} + {x^5} + {x^6} - 1 - x - {x^2} - {x^3} - {x^4} - {x^5} = {x^6} - 1.\)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + 2{y^2} - 2xy + 2x - 10y\)
-
A
$A=3$
-
B
$A=-17$
-
C
$A=-3$
-
D
$A=17$
Đáp án của giáo viên lời giải hay : B
- Tách 1 hạng tử thành nhiều hạng tử hoặc thêm, bớt cùng một hạng tử một cách thích hợp để tách biểu thức đã cho thành dạng $C = a^2 + b^2 + c.$
- Khi đó, \(A \ge c\) với mọi $x.$
- Suy ra, giá trị nhỏ nhất của $A.$
\(\begin{array}{l}\,\,\,\,\,\,\,\,A = {x^2} + 2{y^2} - 2xy + 2x - 10y\\ \Leftrightarrow A = {x^2} + {y^2} + 1 - 2xy + 2x - 2y + {y^2} - 8y + 16 - 17\\ \Leftrightarrow A = \left( {{x^2} + {y^2} + {1^2} - 2.x.y + 2.x.1 - 2.y.1} \right) + \left( {{y^2} - 2.4.y + {4^2}} \right) - 17\\ \Leftrightarrow A = {\left( {x - y + 1} \right)^2} + {\left( {y - 4} \right)^2} - 17.\end{array}\)
Vì \(\left\{ \begin{array}{l}{\left( {x - y + 1} \right)^2} \ge 0\\{\left( {y - 4} \right)^2} \ge 0\end{array} \right.\) với mọi $x;y$ nên \(A \ge - 17\) với mọi $x;y.$
\( \Rightarrow A = - 17 \Leftrightarrow \left\{ \begin{array}{l}x - y + 1 = 0\\y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y - 1\\y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 4\end{array} \right.\)
Vậy $A$ đạt giá trị nhỏ nhất là \(A = - 17\) tại \(\left\{ \begin{array}{l}x = 3\\y = 4\end{array} \right.\).
Cho: \({a^3} + {b^3} + {c^3} = 3abc\) thì
-
A
\(a = b = c\) hoặc \(a + b + c = 0\).
-
B
\(a = b = c\)
-
C
\(a = b = c = 0\)
-
D
\(a = b = c\) hoặc \(a + b + c = 1\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hằng đẳng thức: \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\) để biến đổi giả thiết.
Từ đẳng thức đã cho suy ra \({a^3} + {b^3} + {c^3} - 3abc = 0\)
${b^3} + {c^3} = \left( {b + c} \right)\left( {{b^2} + {c^2} - bc} \right) $$= \left( {b + c} \right)\left[ {{{\left( {b + c} \right)}^2} - 3bc} \right] $$= {\left( {b + c} \right)^3} - 3bc\left( {b + c} \right)$
$ \Rightarrow {a^3} + {b^3} + {c^3} - 3abc $$= {a^3} + \left( {{b^3} + {c^3}} \right) - 3abc $
$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc= {a^3} + {\left( {b + c} \right)^3} - 3bc\left( {b + c} \right) - 3abc$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc $$= \left( {a + b + c} \right)\left( {{a^2} - a\left( {b + c} \right) + {{\left( {b + c} \right)}^2}} \right) - \left[ {3bc\left( {b + c} \right) + 3abc} \right]$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} - a\left( {b + c} \right) + {{\left( {b + c} \right)}^2}} \right) - 3bc\left( {a + b + c} \right)$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} - a\left( {b + c} \right) + {{\left( {b + c} \right)}^2} - 3bc} \right)$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} - ab - ac + {b^2} + 2bc + {c^2} - 3bc} \right)$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - ac - bc} \right)$
Do đó nếu \({a^3} + {b^3} + {c^3} - 3abc = 0\) thì \(a + b + c = 0\) hoặc \({a^2} + {b^2} + {c^2} - ab - bc - ac = 0\)
Mà \({a^2} + {b^2} + {c^2} - ab - bc - ac = \dfrac{1}{2}.\left[ {{{\left( {a - b} \right)}^2} + {{\left( {a - c} \right)}^2} + {{\left( {b - c} \right)}^2}} \right]\) suy ra \(a = b = c\).
