Đề bài
Trong hình thang vuông \(ABCD\) với đáy là \(AD, BC\) có \(\widehat A = \widehat B = 90^\circ \), \(\widehat {ACD} = 90^\circ ,BC = 4cm,AD = 16cm.\) Hãy tìm các góc \(C\) và \(D\) của hình thang.
Phương pháp giải - Xem chi tiết
+) Kẻ thêm hình phụ (kẻ đường cao CH).
+) Sử dụng các tỉ số lượng giác của góc nhọn như sau: \(\tan \alpha = \dfrac{{AB}}{{AC}}\) (hình vẽ)

+) Sử dụng hệ thức lượng trong tam giác vuông \(ABC\) vuông tại \(A\) có chiều cao \(AH\) thì \(AH^2=HB.HC\)
Lời giải chi tiết
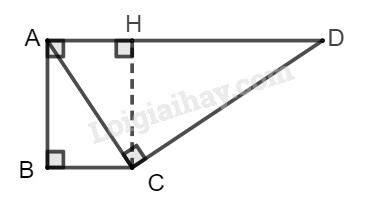
Kẻ đường cao \(CH\) của tam giác \(ACD\) vuông tại C. Khi đó tứ giác \(AHCB\) là hình chữ nhật (vì có ba góc vuông) nên \(AH = BC = 4\), \(HD = AD – AH =16-4= 12.\)
Từ đó, theo hệ thức lượng trong tam giác \(ACD\) vuông, ta có: \(H{C^2} = HA.HD=4.12 = 48\)
Suy ra \(HC = 4\sqrt 3 \).
Trong tam giác vuông \(HCD\), ta có:
\(tgD = \dfrac{{HC}}{{HD}} = \dfrac{{4\sqrt 3 }}{{12}} = \dfrac{{\sqrt 3 }}{3} = tg30^\circ \) nên \(\widehat D = 30^\circ \).
Vì \(AD//BC\) (do ABCD là hình thang) nên \(\widehat {BCD}+\widehat D=180^0\) (hai góc trong cùng phía bù nhau)
Suy ra: \(\widehat {BCD} =180^0-\widehat D= 180^\circ - 30^\circ = 150^\circ .\)
soanvan.me
