Đề bài
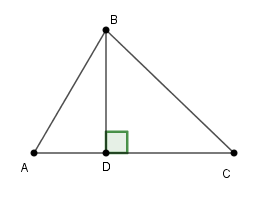
Đường cao \(BD\) của tam giác nhọn \(ABC\) bằng \(6\), đoạn thẳng \(AD = 5\).
a) Tính diện tích tam giác \(ABD\);
b) Tính \(AC\), dùng các thông tin dưới đây nếu cần:
\(\sin C = \dfrac{3}{5},\cos C = \dfrac{4 }{5},tgC = \dfrac{3}{4}.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Công thức tính diện tích tam giác \(ABC\) vuông tại \(A\) và có đường cao \(AH\) là \(S = \dfrac{1}{2}AB.AC = \dfrac{1}{2}AH.BC.\)
Sử dụng tỉ số lượng giác của góc nhọn để tính toán.
Lời giải chi tiết
a) Vì tam giác ABD vuông tại D nên ta có:
\({S_{\Delta ABD}} = \dfrac {1}{ 2}.BD.AD = \dfrac {1}{ 2}.6.5 = 15\) (đvdt)
b) Xét tam giác BCD vuông, theo định nghĩa tỉ số lượng giác của góc nhọn ta có: \(\tan\widehat C = \dfrac {{BD}}{{DC}}\)
Theo giả thiết: \(\tan\widehat C = \dfrac {3}{4}\)
Suy ra: \( \dfrac {{BD}}{{DC}} = \dfrac {3}{4} \Rightarrow DC = \dfrac {4}{3}BD \)\(= \dfrac {{4.6}}{3} = 8\)
Suy ra: \(AC = AD + DC = 5 + 8 = 13.\)
soanvan.me