Xét hình bs. 4. Tìm đẳng thức đúng trong các bài từ 2.9 đến 2.11.
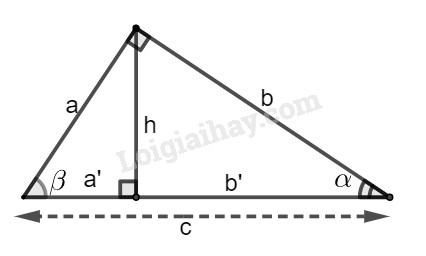
Bài 2.9
(A) \({\cos ^2}\alpha + {\sin ^2}\beta = 1\); (B) \({\sin ^2}\alpha + {\cos ^2}\beta = 1\) ;
(C) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) ; (D) \({\cos ^2}\alpha + {\cos ^2}\beta = 2\).
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết:
Đặt tên hình như hình sau (hình vẽ được sử dụng cho các bài 2.9, 2.10 và 2.11):
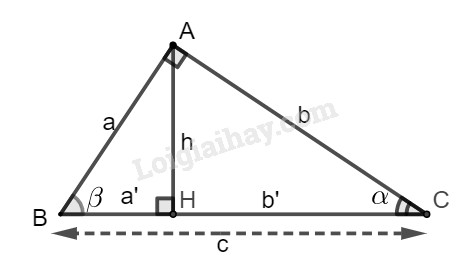
Xét tam giác ABC vuông tại A, ta có: \(a^2+b^2=c^2\) (định lý Pytago) và:
\(\begin{array}{l}
\sin \alpha = \dfrac{a}{c} \Rightarrow {\sin ^2}a = \dfrac{{{a^2}}}{{{c^2}}}\\
\cos \alpha = \dfrac{b}{c} \Rightarrow {\cos ^2}\alpha = \dfrac{{{b^2}}}{{{c^2}}}\\
\Rightarrow {\sin ^2}a + {\cos ^2}\alpha = \dfrac{{{a^2}}}{{{c^2}}} + \dfrac{{{b^2}}}{{{c^2}}} = \dfrac{{{c^2}}}{{{c^2}}} = 1
\end{array}\)
Vậy đáp án là (C)
Bài 2.10
(A) \(tg\alpha = \sin\alpha + \cos\alpha\) ;
(B) \(tg\alpha = \sin\alpha - \cos\alpha\) ;
(C) \(tg\alpha = \sin\alpha .\cos\alpha\) ;
(D) \(tg \alpha\) = \(\dfrac{{\sin \alpha }}{{\cos \alpha }}.\)
Lời giải chi tiết:
\(\begin{array}{l}
\sin \alpha = \dfrac{a}{c};{\rm{cos}}\alpha {\rm{ = }}\dfrac{b}{c}\\
\Rightarrow \dfrac{{\sin \alpha }}{{{\rm{cos}}\alpha }} = \dfrac{a}{c}:\dfrac{b}{c} = \dfrac{a}{b} = tg\alpha
\end{array}\)
Vậy đáp án (D)
Bài 2.11
(A) \(cotg\alpha = 1 + tg\alpha\);
(B) \(cotg\alpha = 1 − tg\alpha\);
(C) \(cotg\alpha = 1.tg\alpha\) ;
(D) \(cotg\alpha = \dfrac{1}{{tg\alpha }}.\)
Lời giải chi tiết:
\(\begin{array}{l}
tg\alpha = \dfrac{a}{b};cotg\,\alpha = \dfrac{b}{a}\\
\Rightarrow tg\alpha .cotg\,\alpha = 1 \Rightarrow cotg\,\alpha = \dfrac{1}{{tg\alpha }}.
\end{array}\)
Vậy đáp án là (D).
soanvan.me
