Đề bài
Các cạnh của một hình chữ nhật bằng \(3\) cm và \(\sqrt 3 \) cm. Hãy tìm các góc hợp bởi đường chéo và các cạnh của hình chữ nhật đó.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất hình chữ nhật và tỉ số lượng giác của góc nhọn: \(\tan \alpha = \dfrac{{AB}}{{AC}}\) (hình vẽ)

Lời giải chi tiết
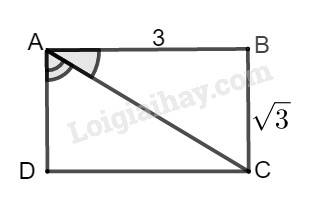
Hình chữ nhật \(ABCD\) có \(AB = 3cm\), \(BC\) = \(\sqrt 3 \) cm
Xét tam giác ABC vuông tại B, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
\(tg\widehat {BAC} = \dfrac{{BC}}{{AB}} = \dfrac{{\sqrt 3 }}{ 3} = tg30^\circ .\)
Vậy \(\widehat {BAC} = 30^\circ \)
Mà \(\widehat {DAC} +\widehat {BAC}=\widehat {BAD}= 90^\circ\)
\(\Rightarrow \widehat {DAC} =90^0-\widehat {BAC}\)\(= 90^\circ - 30^\circ = 60^\circ .\)
Vậy các góc hợp bởi đường chéo và các cạnh của hình chữ nhật đã cho là \(30^0\) và \(60^0.\)
soanvan.me
