Đề bài
Tính các góc của một hình thoi, biết hai đường chéo của nó có độ dài là \(2\sqrt 3 \) và \(2\).
Phương pháp giải - Xem chi tiết
Các tỉ số lượng giác của góc nhọn: \(\tan \alpha = \dfrac{{AB}}{{AC}}\) (hình vẽ)

Sử dụng tính chất: Hình thoi có đường chéo vuông góc với nhau tại trung điểm mỗi đường.
Lời giải chi tiết
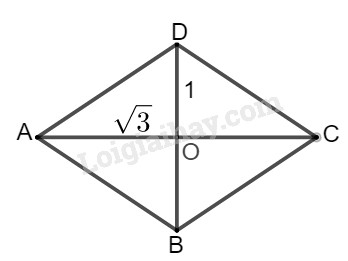
Cho hình thoi \(ABCD\) có đường chéo \(AC = 2\sqrt 3 \), đường chéo \(BD = 2\) thì để ý rằng \(AC\) và \(BD\) vuông góc với nhau tại \(O\) và \(O\) là trung điểm mỗi đường.
Nên \(OD=BD:2=1\) và \(OA=AC:2=\sqrt 3\)
Xét tam giác \(OAD\) vuông tại \(O\), ta có: \(tg\widehat {DAC} = \dfrac{{OD}}{{OA}} = \dfrac{1}{{\sqrt 3 }} = tg30^\circ \) nên \(\widehat {DAC} = 30^\circ \) từ đó góc \(A\) của hình thoi là \(60^0\) (vì đường chéo của hình thoi là phân giác các góc của hình thoi)
Suy ra \(\widehat C = 60^\circ \) còn \(\widehat B = \widehat D\)\(=180^0-60^0 = 120^\circ \) (hai góc kề một cạnh hình thoi có tổng bằng \(180^0.\)
soanvan.me
