Đề bài
Cho đường tròn (O; R), đường kính AB cố định và dây AC. Biết rằng khoảng cách từ O lần lượt đến AC và BC là 8cm và 6cm.
a. Tính độ dài các dây AC, BC và bán kính đường tròn.
b. Lấy D đối xứng với A qua C. Chứng minh ∆ABD cân.
c. Khi C di chuyển trên đường tròn (O). Chứng minh rằng D thuộc một đường tròn cố định.
Phương pháp giải - Xem chi tiết
- Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
- Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương các cạnh góc vuông.
Lời giải chi tiết
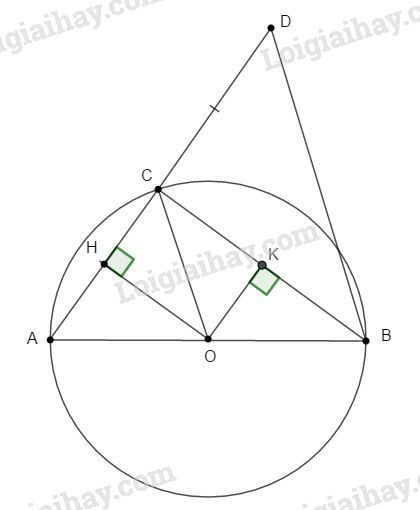
a. Kẻ OH, OK lần lượt vuông góc với AC và BC, ta có:
\(OH = 8cm, OK = 6cm\)
và \(HA = HC = {{AC} \over 2}\)
\(KB = KC = {{BC} \over 2}\) (định lí đường kính và dây cung)
AB là đường kính nên \(\widehat {ACB} = 90^\circ \). Do đó tứ giác CHOK là hình chữ nhật (có ba góc vuông)
\(⇒ OH = CK = 8cm ⇒ BC = 16cm\)
Tương tự có : \(AC = 12cm\)
Xét tam giác vuông OHC, ta có:
\(OC = \sqrt {O{H^2} + H{C^2}} = \sqrt {{8^2} + {6^2}}\)\(\; = 10\,\left( {cm} \right)\) (định lí Pi-ta-go)
b. ∆ABD có đường cao BC đồng thời là đường trung tuyến nên ∆ABD cân tại B.
c. Ta có: \(BD = BA = 2R \) (cmt), B cố định, 2R không đổi.
Vậy D thuộc đường tròn cố định tâm B và bán kính bằng 2R.
soanvan.me
