Đề bài
Cho tam giác ABC vuông tại A có \(AB = 6cm, AC = 8cm\), đường cao AH. Đường tròn (O) đường kính AH cắt AB tại D, đường tròn (O’) đường kính CH cắt AC tại E.
a. Chứng minh (O) và (O’) cắt nhau tại hai điểm phân biệt.
b. Chứng minh đường thẳng DE là tiếp tuyến của (O’).
Phương pháp giải - Xem chi tiết
a.Sử dụng:
+Định lý Py-ta-go
+Hệ thức và cạnh và đường cao trong tam giác vuông
+Đường trung bình của tam giác bằng nửa cạnh đáy
b.Sử dụng:
+Tính chất hình chữ nhật
+Tính chất tam giác cân
Chứng minh tổng hai góc OEH và O'EH bằng 90 độ
Lời giải chi tiết
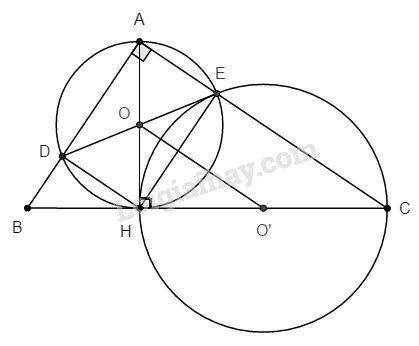
a. ∆ABC vuông tại A, ta có: \(BC = \sqrt {A{B^2} + A{C^2}} \)\(\;= \sqrt {{6^2} + {8^2}} = 10\,\left( {cm} \right)\)
Lại có: \(AH.BC = AB.AC\) (hệ thức lượng)
\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{6.8} \over {10}} = 4,8\,\left( {cm} \right)\)
Do đó bán kính của (O) là : \(R = 2,4\) (cm)
Ta có: \(A{C^2} = BC.HC\) (hệ thức lượng)
\( \Rightarrow HC = {{A{C^2}} \over {BC}} = {{{8^2}} \over {10}} = 6,4\,\left( {cm} \right)\)
nên bán kính của (O’) là \(R’ = 3,2cm\)
Mặt khác: OO’ là đường trung bình của ∆AHC
nên \(OO' = {1 \over 2}AC = {1 \over 2}.8 = 4\,\left( {cm} \right)\)
Ta có: \(OO’ < R + R’\; (4 < 2,4 + 3,2)\) chứng tỏ (O) và (O’) cắt nhau tại hai điểm phân biệt.
b. Ta có: \(\widehat {ADH} = \widehat {AEH} = 90^\circ \) (AH là đường kính) và \(\widehat {BAC} = 90^\circ \) (gt) nên ADHE là hình chữ nhật (có ba góc vuông).
O là giao điểm hai đường chéo AH và \(DE, OH = OE ⇒ ∆OHE\) cân tại O
\( \Rightarrow \widehat {OHE} = \widehat {OEH}\)
Mặt khác, ∆O’HE cân tại O’ (\(O’H = O’E = R’\))
\( \Rightarrow \widehat {O'HE} = \widehat {O'EH},\) mà \(\widehat {OHE} + \widehat {O'HE} = 90^\circ \) (gt)
Do đó \(\widehat {OEH} + \widehat {O'EH} = 90^\circ \) hay \(OE ⊥ O’E\).
\(⇒ DE\) là tiếp tuyến của đường tròn (O’).
soanvan.me
