Đề bài
Cho hình thang cân ABCD \(\left( {AB\parallel CD} \right)\) có AB = AD và BD = CD. Hãy tính các góc của hình thang cân.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tam giác cân và tổng ba góc trong tam giác bằng \(180^0\)
Lời giải chi tiết
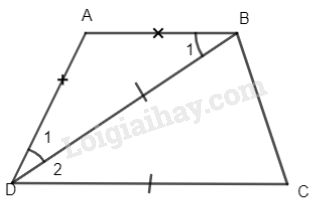Ta có: AB = AD (gt) nên \(\Delta ABD\) cân \( \Rightarrow \widehat {{B_1}} = \widehat {{D_1}}\)Lại có: \(AB// CD(gt) \Rightarrow \widehat {{B_1}} = \widehat {{D_2}}\)(so le trong)
\( \Rightarrow \widehat {{D_1}} = \widehat {{D_2}}\) hay DB là phân giác của \(\widehat {ADC}\)
\(\Delta BCD\) cân (gt) \( \Rightarrow \widehat {BCD} = \widehat {CBD} = \dfrac{{{{180}^ \circ } - \widehat {{D_2}}} }{ 2}\)
\( \Rightarrow 2\widehat {BCD} = {180^ \circ } - \widehat {{D_2}}\)
\( \Rightarrow 2\widehat {ADC} = {180^ \circ } - \widehat {{D_2}}\left( {\widehat {ADC} = \widehat {BCD}} \right)\)
\( \Rightarrow 2.2\widehat {{D_2}} = {180^ \circ } - \widehat {{D_2}}\left( {\widehat {ADC} = 2\widehat {{D_2}}} \right)\)
\( \Rightarrow 5\widehat {{D_2}} = {180^ \circ } \Rightarrow \widehat {{D_2}} = {36^ \circ }\)
\( \Rightarrow \widehat {ADC} = 2\widehat {{D_2}} = {72^ \circ }\) và \(\widehat {BCD} = {72^ \circ }\)
\( \Rightarrow \widehat {BAD} = \widehat {ABC} = {180^ \circ } - {72^ \circ } = {108^ \circ }\)
soanvan.me