Đề bài
Cho hình thang ABCD \(\left( {AB// CD} \right)\) có \(\widehat A - \widehat D = {40^ \circ }\) và \(\widehat B = 3\widehat C\) Hãy tính các góc của hình thang.
Phương pháp giải - Xem chi tiết
Sử dụng: Tổng bốn góc trong tứ giác bằng \(360^0\)
Hai góc kề cạnh bên của hình thang có tổng bằng \(180^0\)
Lời giải chi tiết
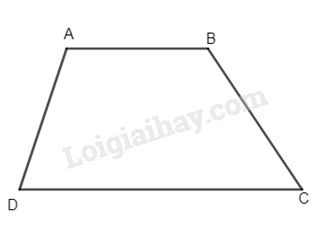
Ta có \(\widehat A - \widehat D = {40^ \circ }(gt) \Rightarrow \widehat A = {40^ \circ } + \widehat D(1)\)
\(AB//CD\;(gt) \Rightarrow \widehat A + \widehat D = {180^ \circ }(2)\)
Thế (1) vào (2) ta có: \({40^ \circ } + \widehat D + \widehat D = {180^ \circ }\)
\( \Rightarrow 2\widehat D = {180^ \circ } - {40^ \circ } \)
\(\Rightarrow \widehat D = {70^ \circ } \Rightarrow \widehat A = {110^ \circ }\)
Lại có: \(\widehat B + \widehat C = {180^ \circ }\) mà \(\widehat B = 3\widehat C(gt) \Rightarrow 3\widehat C + \widehat C = {180^ \circ }\)
\( \Rightarrow 4\widehat C = {180^ \circ } \Rightarrow \widehat C = {45^ \circ }\)
Do đó: \(\widehat B = {3.45^ \circ } = {135^ \circ }\)
soanvan.me
