Đề bài
Cho hình bình hành ABCD. Trên các cạnh AB, BC, CD, DA lấy các điểm I, J, K, L sao cho AI = BJ = CK = DL. Chứng minh rằng:
a) Tứ giác IJKL là hình bình hành.
b) Bốn đường thẳng AC, BD, IK, JK đồng quy.
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành
Hai đường chéo của hình bình hành giao nhau tại trung điểm mỗi đường
Lời giải chi tiết
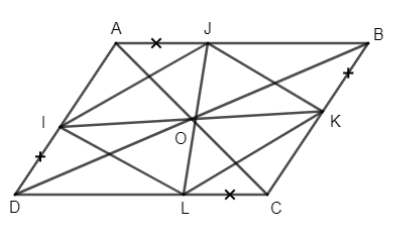
a) Ta có \(\Delta IBJ = \Delta KDL(c.g.c)\) và \(\Delta JCK = \Delta LAI\)
\( \Rightarrow {\rm{IJ}} = KL\) và JK = IL.
Vậy tứ giác IJKL là hình bình hành (các cạnh đối bằng nhau).
b) Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD ta có O là trung điểm của AC. Lại có tứ giác AICK là hình bình hành \((AI//CK\) và \(AI = CK) \Rightarrow \) đường chéo IK đi qua trung điểm O của AC, tứ giác IJKL là hình bình hành (cmt) \( \Rightarrow \) đường chéo JL đi qua trung điểm O của đường chéo IK. Vậy bốn đường thẳng AC, BD, IK, JL đồng quy.
soanvan.me
