Đề bài
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của hai cạnh AB và AC và I là trung điểm của MN. Gọi J là điểm đối xứng của A qua I. Chứng minh rằng B đối xứng với C qua J.
Phương pháp giải - Xem chi tiết
Sử dụng:
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
Lời giải chi tiết
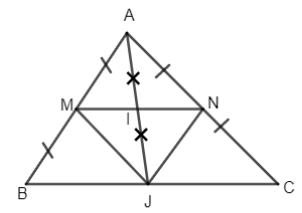
M, I lần lượt là trung điểm của AB và AJ (gt)
\( \Rightarrow MI\) là đường trung bình của \(\Delta ABJ\)
\( \Rightarrow MI// BJ\) hay \(MN// BJ.\)
Tương tự có MN là đường trung bình của \(\Delta ABC\) (vì M, N lần lượt là trung điểm của AB, AC)
Suy ra \(MN// CJ\) mà \(MN//BC\)
\( \Rightarrow B,J,C\) thẳng hàng (1)
Lại có BJ = 2MI; tương tự CJ = 2NI mà MI = NI (gt)
\( \Rightarrow BJ = CJ\) (2)
Từ (1) và (2) suy ra B đối xứng với C qua J.
soanvan.me
