Đề bài
Cho hình thang cân ABCD \(\left( {AB//CD} \right)\) có \(\widehat D = {60^ \circ },AD = AB\)
a)Chứng minh rằng: BD là tia phân giác của góc ADC.
b)Chứng minh: \(BD \bot BC\)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tam giác cân và tính chất hai đường thẳng song song.
Trong hình thang cân, hai góc kề cạnh đáy bằng nhau.
Lời giải chi tiết
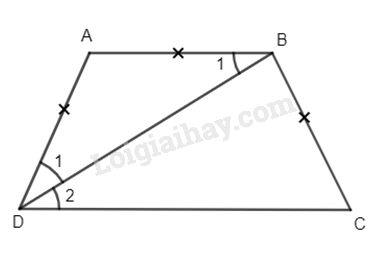
a) Ta có: \(\widehat {{B_1}} = \widehat {{D_2}}\) (AB//CD, so le trong) (1)
\(AB = AD(gt)\) nên \(\Delta ABD\) cân tại A
\( \Rightarrow \widehat {{B_1}} = \widehat {{D_1}}\) (2)
Từ (1) vào (2) suy ra \(\widehat {{D_1}} = \widehat {{D_2}}\) hay BD là tia phân giác của góc ADC.
b) Ta có: \(\widehat {BCD} = \widehat {ADC} = {60^ \circ }\) (hai góc kề đáy của hình thang cân)
mà BD là tia phân giác của góc ADC nên \(\widehat {{D_1}} = \widehat {{D_2}} = {30^ \circ }\)
Trong \(\Delta DBC\) ta có \(\widehat {DBC} = {180^ \circ } - \left( {\widehat {{D_2}} + \widehat {BCD}} \right)\)
\(\widehat {DBC} = {180^ \circ } - \left( {{{30}^ \circ } + {{60}^ \circ }} \right)\)
\(\widehat {DBC} = {90^ \circ },\) chứng tỏ \(BD \bot BC\)
soanvan.me
