Đề bài
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC.
a) Chứng minh EF = AH.
b) Kẻ trung tuyến AM của tam giác ABC. Chứng minh \(AM \bot EF.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có ba góc vuông là hình chữ nhật.
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
Tính chất hình chữ nhật và định lý tổng ba góc trong tam giác
Lời giải chi tiết
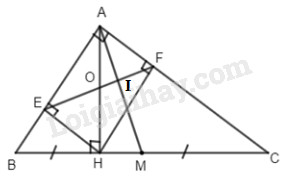
a) Dễ thấy AEHF là hình chữ nhật (có ba góc vuông)
\( \Rightarrow EF = AH\) (tính chất hai đường chéo của hình chữ nhật).
b) Xét tam giác ABC vuông tại A có AM là đường trung tuyến nên \(AM = MC = \dfrac{1 }{ 2}BC\) (đường trung tuyến của tam giác vuông bằng nửa cạnh huyền)
\( \Rightarrow \Delta AMC\) cân tại M nên \(\widehat {MAC} = \widehat C.\)
Mặt khác AEHF là hình chữ nhật (cmt)
\( \Rightarrow OA = OF\) hay \(\Delta AOF\) cân
\( \Rightarrow \widehat {OAF} = \widehat {OFA}\) mà \(\widehat {OAF} = \widehat B\) (cùng phụ với \(\widehat C\)) \( \Rightarrow \widehat {OFA} = \widehat B.\)
\(\Delta ABC\) vuông tại A có \(\widehat B + \widehat C = {90^ \circ } \Rightarrow \widehat {OFA} + \widehat {MAC} = {90^ \circ }\)
Gọi I là giao điểm của AM và EF. Xét tam giác AIF có \(\widehat {IFA} + \widehat {IAF} = {90^ \circ }\)
\( \Rightarrow \widehat {AIF} = {90^ \circ }\) hay \(AI \bot IF\)
Vậy \(AM \bot EF\) (đpcm)
soanvan.me
