Một mạch điện xoay chiều có u là điện áp tức thời ở hai đầu đoạn mạch và i là cường độ tức thời qua mạch. Chọn phát biểu đúng:
-
A
u và i luôn luôn biến thiên cùng tần số.
-
B
u và i luôn luôn biến thiên cùng pha.
-
C
u và i luôn luôn biến thiên ngược pha.
-
D
u luôn luôn sớm pha hơn i.
Đáp án của giáo viên lời giải hay : A
A - đúng
B, C, D - sai vì tùy loại mạch mà u và i có độ lệch pha khác nhau
Chọn phát biểu sai:
-
A
Dòng điện xoay chiều qua điện trở thuần R chỉ có tác dụng nhiệt.
-
B
Điện áp ở hai đầu đoạn mạch chỉ có điện trở thuần biến thiên điều hòa cùng tần số với cường độ dòng điện.
-
C
Cường độ dòng điện qua đoạn mạch chỉ có điện trở thuần biến thiên điều hòa cùng pha với điện áp.
-
D
Nhiệt lượng tỏa ra ở điện trở thuần tỉ lệ với cường độ hiệu dụng qua nó.
Đáp án của giáo viên lời giải hay : D
A, B, C - đúng
D - sai vì Nhiệt lượng tỏa ra ở điện trở thuần tỉ lệ với bình phương cường độ hiệu dụng qua nó
\(Q = {I^2}Rt = \frac{{I_0^2Rt}}{2}\)
Điều nào sau đây là đúng khi nói về đoạn mạch xoay chiều chỉ có điện trở thuần?
-
A
Dòng điện qua điện trở và điện áp hai đầu điện trở luôn cùng pha.
-
B
Pha của dòng điện qua điện trở luôn bằng không.
-
C
Mối liên hệ giữa cường độ dòng điện và điện áp hiệu dụng là U = I/R.
-
D
Nếu điện áp ở hai đầu điện trở là
\(u = {U_0}\sin (\omega t + \varphi )(V) \to i = {I_0}\sin (\omega t)(A)\)
Đáp án của giáo viên lời giải hay : A
Phương án B sai vì pha của dòng điện bằng với pha của điện áp chứ không phải luôn bằng 0.
Phương án C sai vì biểu thức định luật Ohm là U = I.R
Phương án D sai vì dòng điện và điện áp cùng pha nên
\(u = {U_0}\sin (\omega t + \varphi )(V) \to i = {I_0}\sin (\omega t + \varphi)(A)\)
Đặt vào hai đầu đoạn mạch chỉ có điện trở thuần R một điện áp xoay chiều có biểu thức u = U0cos(ωt) V thì cường độ dòng điện chạy qua điện trở có biểu thức i = I\(\sqrt 2 \)cos(ωt+ $\varphi $i) A, trong đó I và $\varphi $i được xác định bởi các hệ thức tương ứng là
-
A
\(I{\rm{ }} = \frac{{{U_0}}}{R};{\varphi _i} = \frac{\pi }{2}\)
-
B
\(I{\rm{ }} = \frac{{{U_0}}}{{2R}};{\varphi _i} = 0\)
-
C
\(I{\rm{ }} = \frac{{{U_0}}}{{\sqrt 2 R}};{\varphi _i} = - \frac{\pi }{2}\);
-
D
\(I{\rm{ }} = \frac{{{U_0}}}{{\sqrt 2 R}};{\varphi _i} = {\rm{ }}0\)
Đáp án của giáo viên lời giải hay : D
+ Vận dụng biểu thức xác định cường độ dòng điện hiệu dụng trong mạch chỉ có điện trở R
+ Sử dụng lí thuyết về độ lệch pha của cường độ dòng điện và điện áp trong mạch chỉ có R
Ta có:
+ Cường độ dòng điện hiệu dụng trong mạch chỉ có R:
\(I{\rm{ }} = \frac{U}{R} = \frac{{{U_0}}}{{\sqrt 2 R}}\)
+ Cường độ dòng điện và hiệu điện thế trong mạch chỉ có R dao động cùng pha với nhau => $\varphi $i = $\varphi $u = 0
Đoạn mạch điện xoay chiều gồm hai điện trở thuần R1 = 20 Ω và R2 = 40 Ω mắc nối tiếp với nhau. Đặt vào giữa hai đầu đoạn mạch một điện áp xoay chiều có biểu thức u = 120\(\sqrt 2 \)cos100πt V. Kết luận nào sau đây là không đúng ?
-
A
Dòng điện xoay chiều chạy qua hai điện trở thuần cùng pha với nhau.
-
B
Dòng điện xoay chiều chạy qua hai điện trở thuần có cùng cường độ hiệu dụng I = 2 A.
-
C
Dòng điện xoay chiều chạy qua hai điện trở thuần có biểu thức i = 2\(\sqrt 2 \)cos100πt A.
-
D
Dòng điện xoay chiều chạy qua hai điện trở thuần R1 và R2 có cường độ cực đại lần lượt là I01 = 6\(\sqrt 2 \) A; I02 = 3\(\sqrt 2 \) A
Đáp án của giáo viên lời giải hay : D
+ Áp dụng biểu thức tính tổng trở trong mạch: R = R1+R2
+ Áp dụng biểu thức tính cường độ dòng điện hiệu dụng:
\(I{\rm{ }} = \frac{U}{R}\)
+ Áp dụng biểu thức tính cường độ dòng điện cực đại:
\({I_0}{\rm{ }} = \frac{{{U_0}}}{R}\)
+ Sử dụng lí thuyết về độ lệch pha của cường độ dòng điện và điện áp trong mạch chỉ có R
Ta có tổng trở của mạch: R = R1 + R2 = 60Ω
Cường độ dòng điện hiệu dụng trong mạch:
\(I{\rm{ }} = \frac{U}{R} = \frac{{120}}{{60}} = 2A\)
Cường độ dòng điện cực đại qua R1 và R2 là như nhau và bằng:
\({I_{01}}{\rm{ = }}{{\rm{I}}_{02}} = {I_0} = \frac{{{U_0}}}{R} = \frac{{120\sqrt 2 }}{{60}} = 2\sqrt 2 A\)
Cường độ dòng điện và hiệu điện thế trong mạch dao động cùng pha nhau
=> Biểu thức cường độ dòng điện trong mạch:
\(i = 2\sqrt 2 {\rm{cos100}}\pi t\)
Mắc điện trở \(R = 55\Omega \)vào mạng điện xoay chiều có điện áp \(u = 110\cos \left( {100\pi t + \pi /2} \right)(V)\). Nhiệt lượng toả ra ở $R$ trong $10$ phút là:
-
A
132 kJ
-
B
66 kJ
-
C
33000 J
-
D
13,2 kJ
Đáp án của giáo viên lời giải hay : B
+ Áp dụng biểu thức tính cường độ dòng điện cực đại trong mạch chỉ có điện trở:
\({I_0} = \frac{{{U_0}}}{R}\)
+ Áp dụng biểu thức tính nhiệt lượng tỏa ra:
\(Q = {I^2}Rt = \dfrac{{I_0^2Rt}}{2}\)
Ta có, cường độ dòng điện cực đại trong mạch:
\({I_0} = \dfrac{{{U_0}}}{R} = \dfrac{{110}}{{55}} = 2A\)
Nhiệt lượng tỏa ra trên R trong 10 phút là:
\(Q = {I^2}Rt = \dfrac{{I_0^2Rt}}{2} = \dfrac{{{2^2}.55.10.60}}{2} = 66000J = 66kJ\)
Một cuộn dây thuần cảm có độ tự cảm L được mắc vào điện áp xoay chiều u có tần số f. Chọn phát biểu đúng:
-
A
Cường độ dòng điện biến thiên điều hòa cùng pha với điện áp u.
-
B
Cường độ hiệu dụng qua mạch tỉ lệ nghịch với f.
-
C
Cường độ dòng điện qua mạch tỉ lệ thuận với L.
-
D
Cường độ dòng điện biến thiên điều hòa với tần số f’ = 2f
Đáp án của giáo viên lời giải hay : B
A- sai vì: Cường độ dòng điện trong mạch chỉ có L trễ pha hơn điện áp u
B- đúng
C- sai vì:
\(I = \frac{U}{{{Z_L}}} = \frac{U}{{\omega L}} = \frac{U}{{2\pi fL}}\)
=> cường độ dòng điện tỉ lệ nghịch với L và f
D- sai vì cường độ dòng điện biến thiên điều hòa với tần số f
Tác dụng của cuộn cảm đối với dòng điện xoay chiều là:
-
A
Gây cảm kháng nhỏ nếu tần số dòng điện lớn.
-
B
Ngăn cản hoàn toàn dòng điện xoay chiều.
-
C
Gây cảm kháng lớn nếu tần số dòng điện lớn.
-
D
Chỉ cho phép dòng điện đi qua theo một chiều.
Đáp án của giáo viên lời giải hay : C
Ta có, cảm kháng:
\({Z_L} = 2\pi fL\)
=> cảm kháng lớn nếu tần số dòng điện lớn
Một mạch điện xoay chiều chỉ chứa cuộn cảm, $i$ là cường độ dòng điện tức thời qua mạch và $u$ là điện áp tức thời. Chọn câu đúng:
-
A
i sớm pha hơn u là \(\dfrac{\pi }{2}\)
-
B
u trễ pha hơn i là \(\dfrac{\pi }{4}\)
-
C
u sớm pha hơn i là \(\dfrac{\pi }{2}\)
-
D
i trễ pha hơn u là \(\dfrac{\pi }{4}\)
Đáp án của giáo viên lời giải hay : C
Trong mạch xoay chiều chỉ có cuộn cảm thì điện áp nhanh pha hơn dòng điện góc π/2:
\(\varphi \)u = \(\varphi \)i + π/2
Cho L là độ tự cảm, f là tần số, T là chu kì, \(\omega \) là tần số góc. Biểu thức tính cảm kháng của cuộn cảm là:
-
A
\({Z_L} = \frac{1}{{\omega L}}\)
-
B
\({Z_L} = 2\pi fL\)
-
C
\({Z_L} = 2\pi TL\)
-
D
\({Z_L} = \frac{{TL}}{{2\pi }}\)
Đáp án của giáo viên lời giải hay : B
Cảm kháng của cuộn cảm được xác định bởi biểu thức:
\({Z_L} = \omega L = 2\pi fL\)
Mạch điện xoay chiều chỉ có cuộn thuần cảm với độ tự cảm L. Đặt vào hai đầu cuộn thuần cảm một điện áp xoay chiều u = U\(\sqrt 2 \)cos(ωt + \(\varphi \)) V. Cường độ dòng điện cực đại của mạch được cho bởi công thức:
-
A
\({I_0} = \dfrac{U}{{\sqrt 2 \omega L}}\)
-
B
\({I_0} = \dfrac{U}{{\omega L}}\)
-
C
\({I_0} = \dfrac{{U\sqrt 2 }}{{\omega L}}\)
-
D
\({I_0} = U\sqrt 2 \omega L\)
Đáp án của giáo viên lời giải hay : C
Với đoạn mạch chỉ có L thì
\({I_0} = \dfrac{{{U_0}}}{{{Z_L}}} = \dfrac{{U\sqrt 2 }}{{\omega L}}\)
Đặt vào hai đầu cuộn cảm \(L = 1/\pi \) H một điện áp xoay chiều $220V – 50Hz$. Cảm kháng của cuộn cảm là:
-
A
\(50\Omega \)
-
B
\(5\Omega \)
-
C
\(100\Omega \)
-
D
\(10\Omega \)
Đáp án của giáo viên lời giải hay : C
Áp dụng biểu thức xác định cảm kháng: \({Z_L} = \omega L = 2\pi fL\)
Ta có, cảm kháng của cuộn cảm:
\({Z_L} = \omega L = 2\pi fL = 2\pi .50.\dfrac{1}{\pi } = 100\Omega \)
Đoạn mạch điện xoay chiều chỉ có cuộn cảm có hệ số tự cảm $L$. Điện áp tức thời và cường độ dòng điện tức thời của mạch là $u$ và $i$. Điện áp hiệu dụng và cường độ hiệu dụng là $U, I$. Biểu thức nào sau đây là đúng?
-
A
\({\left( {\dfrac{u}{U}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 1\)
-
B
\({\left( {\dfrac{u}{U}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 2\)
-
C
\({\left( {\dfrac{u}{U}} \right)^2} - {\left( {\dfrac{i}{I}} \right)^2} = 0\)
-
D
\({\left( {\dfrac{u}{U}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = \dfrac{1}{2}\)
Đáp án của giáo viên lời giải hay : B
Mạch chỉ có cuộn cảm nên điện áp nhanh pha hơn dòng điện góc $\dfrac{\pi}{2}$
Khi đó ta có
\(\begin{array}{l}\left\{ \begin{array}{l}u = {U_C}\cos (\omega t + {\varphi _u}) = U\sqrt 2 \cos (\omega t + {\varphi _u})\\i = {I_0}\cos (\omega t + {\varphi _u} - \dfrac{\pi }{2}) = I\sqrt 2 \sin (\omega t + {\varphi _u})\end{array} \right.\\ \to {\left( {\dfrac{u}{{U\sqrt 2 }}} \right)^2} + {\left( {\dfrac{i}{{I\sqrt 2 }}} \right)^2} = 1\\ \leftrightarrow {\left( {\dfrac{u}{U}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 2\end{array}\)
Cho một đoạn mạch điện xoay chiều chỉ có cuộn cảm thuần. Tại thời điểm t1 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 25 V; 0,3 A. Tại thời điểm t2 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 15 V; 0,5 A. Cảm kháng của mạch có giá trị là:
-
A
30 Ω.
-
B
50 Ω.
-
C
40 Ω.
-
D
100 Ω.
Đáp án của giáo viên lời giải hay : B
+ Áp dụng hệ thức: \({\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 1\)
+ Áp dụng công thức tính cảm kháng:
\({Z_L} = \dfrac{{{U_0}}}{{{I_0}}}\)
Ta có:
Mạch chỉ có cuộn cảm nên điện áp nhanh pha hơn dòng điện góc π/2.
Khi đó ta có: \({\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 1\)
Tại thời điểm t1:
\({\left( {\dfrac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_1}}{{{I_0}}}} \right)^2} = 1\)
Tại thời điểm t2:
\({\left( {\dfrac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_2}}{{{I_0}}}} \right)^2} = 1\)
Từ đó ta được:
\({\left( {\dfrac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_1}}{{{I_0}}}} \right)^2} = {\left( {\dfrac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_2}}{{{I_0}}}} \right)^2} \to \dfrac{{u_1^2 - u_2^2}}{{U_0^2}} = \dfrac{{i_2^2 - i_1^2}}{{I_0^2}} \to \dfrac{{{U_0}}}{{{I_0}}} = \sqrt {\dfrac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \)
Mặt khác, ta có:
\({Z_L} = \dfrac{{{U_0}}}{{{I_0}}} = \sqrt {\dfrac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \) .
Thay số ta được ZL = 50 W
Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Tần số của dòng điện trong mạch là f, công thức đúng để tính dung kháng của mạch là
-
A
ZC = 2πfC
-
B
ZC = πfC
-
C
\({Z_C} = \frac{1}{{2\pi fC}}\)
-
D
\({Z_C} = \frac{1}{{\pi fC}}\)
Đáp án của giáo viên lời giải hay : C
Dung kháng của mạch được xác định bằng biểu thức:
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\)
Chọn câu đúng trong các phát biểu sau đây ?
-
A
Tụ điện cho cả dòng điện xoay chiều và dòng điện một chiều đi qua.
-
B
Điện áp giữa hai bản tụ biến thiên sớm pha π/2 đối với dòng điện.
-
C
Cường độ hiệu dụng của dòng điện xoay chiều qua tụ điện tỉ lệ nghịch với tần số dòng điện.
-
D
Dung kháng của tụ điện tỉ lệ thuận với chu kỳ của dòng điện xoay chiều.
Đáp án của giáo viên lời giải hay : D
A - sai vì tụ điện không cho dòng một chiều đi qua
B - sai vì điện áp giữa hai bản tụ biến thiên trễ pha π/2 đối với dòng điện
C - sai vì cường độ dòng điện tỉ lệ thuận với tần số dòng điện:
\(I = \frac{U}{{{Z_C}}} = \frac{U}{{\frac{1}{{\omega C}}}} = U\omega C = U2\pi fC\)
D - đúng
Đặt vào hai đầu tụ điện \(C=\dfrac{{{{10}^{ - 4}}}}{\pi }\)(F) một điện áp xoay chiều \(u = 141cos(100πt) V\). Dung kháng của tụ điện có giá trị là:
-
A
ZC = 50Ω
-
B
ZC = 0,01 Ω
-
C
ZC = 1 Ω
-
D
ZC = 100 Ω
Đáp án của giáo viên lời giải hay : D
Áp dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
Dung kháng:
\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
Với mạch điện xoay chiều chỉ chứa tụ điện thì dòng điện trong mạch
-
A
Sớm pha hơn điện áp ở hai đầu đoạn mạch góc π/2.
-
B
Sớm pha hơn điện áp ở hai đầu đoạn mạch góc π /4.
-
C
Trễ pha hơn điện áp ở hai đầu đoạn mạch góc π /2.
-
D
Trễ pha hơn điện áp ở hai đầu đoạn mạch góc π /4.
Đáp án của giáo viên lời giải hay : A
Trong mạch xoay chiều chỉ có tụ điện thì dòng điện trong mạch sớm pha hơn điện áp ở hai đầu đoạn mạch một góc π /2
Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Đặt vào hai đầu tụ điện một điện áp u = U0cos(ωt + \(\varphi \)) V. Cường độ dòng điện hiệu dụng của mạch được cho bởi công thức:
-
A
\(I = \dfrac{{{U_0}}}{{\sqrt 2 \omega C}}\)
-
B
\(I = \dfrac{{{U_0}\omega C}}{{\sqrt 2 }}\)
-
C
\(I = \dfrac{{{U_0}}}{{\omega C}}\)
-
D
\(I = {U_0}\omega C\)
Đáp án của giáo viên lời giải hay : B
Ta có: Cường độ dòng điện hiệu dụng trong mạch:
\(I = \dfrac{U}{{{Z_C}}} = \dfrac{U}{{\dfrac{1}{{\omega C}}}} = U\omega C = \dfrac{{{U_0}}}{{\sqrt 2 }}\omega C\)
Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Đặt vào hai đầu tụ điện một điện áp xoay chiều có biểu thức u = U0cos(ωt + \(\varphi \)) V. Cường độ dòng điện tức thời của mạch có biểu thức là
-
A
i = U0ωCsin($\omega $t + $\varphi $ + $\frac{\pi }{2}$ ) A
-
B
i = U0ωCcos($\omega $t + $\varphi $ - $\frac{\pi }{2}$ ) A
-
C
i = U0ωCcos($\omega $t + $\varphi $ + $\frac{\pi }{2}$ ) A
-
D
i = \(\frac{{{U_0}}}{{C\omega }}\)cos(($\omega $t + $\varphi $ + $\frac{\pi }{2}$) A.
Đáp án của giáo viên lời giải hay : C
+ Áp dụng biểu thức tính cường độ dòng điện cực đại trong mạch chỉ có tụ điện
+ Sử dụng lí thuyết về độ lệch pha u-i trong mạch chỉ có tụ điện
Ta có,
+ Cường độ dòng điện cực đại:
\({I_0} = \frac{{{U_0}}}{{{Z_C}}} = \frac{{{U_0}}}{{\frac{1}{{\omega C}}}} = {U_0}\omega C\)
+ Cường độ dòng điện trong mạch sớm pha p/2 so với điện áp đặt vào hai đầu tụ điện
Cho đoạn mạch điện xoay chiều chỉ có tụ điện với điện dung C = \(\dfrac{{{{10}^{ - 4}}}}{\pi }\)(F). Đặt điện áp xoay chiều có tần số $50 Hz$ vào hai đầu đoạn mạch. Tại thời điểm mà điện áp hai đầu mạch có giá trị 100 \(\sqrt {10} \) V thì cường độ dòng điện trong mạch là \(\sqrt 2 A\). Điện áp hiệu dụng hai đầu tụ điện có giá trị là:
-
A
UC = $100\sqrt 2 $ V.
-
B
UC = $100\sqrt 6 $ V.
-
C
UC = $100\sqrt 3 $ V.
-
D
UC = $200\sqrt 2 $ V.
Đáp án của giáo viên lời giải hay : B
+ Áp dụng công thức tính dung khác :
\({Z_C} = \dfrac{1}{{\omega C}}\)
+ Áp dụng hệ thức liên hệ ta được:
\({\left( {\dfrac{{{u_C}}}{{{U_{0C}}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\)
+ Áp dụng mối liên hệ giữa cường U0 - I0 - ZC:
\({Z_C} = \dfrac{{{U_0}}}{{{I_0}}}\)
Dung kháng của mạch là :
\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
Áp dụng hệ thức liên hệ ta được:
\(\begin{array}{l}{\left( {\dfrac{{{u_C}}}{{{U_{0C}}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1 \leftrightarrow {\left( {\frac{{100\sqrt {10} }}{{100{I_0}}}} \right)^2} + {\left( {\dfrac{{\sqrt 2 }}{{{I_0}}}} \right)^2} = 1 \leftrightarrow \dfrac{{10}}{{I_0^2}} + \dfrac{2}{{I_0^2}} = 1\\ \to {I_0} = 2\sqrt 3 A \to {U_{0C}} = {I_0}{Z_C} = 200\sqrt 3 V \to {U_C} = \dfrac{{{U_{0C}}}}{{\sqrt 2 }} = \dfrac{{200\sqrt 3 }}{{\sqrt 2 }} = 100\sqrt 6 V\end{array}\)
Cho đoạn mạch điện xoay chiều chỉ có tụ điện với điện dung C. Tại thời điểm t1 điện áp và dòng điện qua tụ điện có giá trị lần lượt là 40 V; 1 A. Tại thời điểm t2 điện áp và dòng điện qua tụ điện có giá trị lần lượt là 50 V ; 0,6 A. Dung kháng của mạch có giá trị là
-
A
30 Ω
-
B
40 Ω
-
C
50 Ω
-
D
37,5 Ω
Đáp án của giáo viên lời giải hay : D
+ Sử dụng hệ thức
\({\left( {\frac{u}{{{U_0}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\)
+ Áp dụng mối liên hệ giữa cường U0 - I0 - ZC:
\({Z_C} = \frac{{{U_0}}}{{{I_0}}}\)
Áp dụng hệ thức liên hệ ta được:
\({\left( {\frac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{i{}_1}}{{{I_0}}}} \right)^2} = {\left( {\frac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{i{}_2}}{{{I_0}}}} \right)^2} \leftrightarrow \frac{{{U_0}}}{{{I_0}}} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \)
Mặt khác, ta có:
\({Z_C} = \frac{{{U_0}}}{{{I_0}}} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \)
Thay số ta được ZC = 37, 5 Ω
Đặt vào hai đầu cuộn cảm có điện trở thuần một điện áp xoay chiều \(u = 120\cos 100\pi t\left( V \right)\). Biểu thức của cường độ dòng điện trong đoạn mạch là \(i = 3\cos \left( {100\pi t - \frac{\pi }{6}} \right){\rm{ }}A\). Độ tự cảm L của cuộn dây gân nhất với giá trị nào sau đây?
-
A
95 mH.
-
B
105 mH.
-
C
45 mH.
-
D
65mH.
Đáp án của giáo viên lời giải hay : D
Biểu thức định luật Ôm:
\({I_0} = \frac{{{U_0}}}{Z} \Rightarrow Z = \frac{{{U_0}}}{{{I_0}}}\)
Độ lệch pha giữa u và i:
\(\tan \varphi = \frac{{{Z_L}}}{R}\)
Biểu thức tính tổng trở:
\(Z = \sqrt {{R^2} + Z_L^2} \)
Công thức tính cảm kháng:
\({Z_L} = \omega L\)
+ Ta có:
\({I_0} = \frac{{{U_0}}}{Z} \Rightarrow Z = \frac{{{U_0}}}{{{I_0}}} = \frac{{120}}{3} = 40\Omega \)
+ Độ lệch pha giữa u và i:
\(\tan \varphi = \frac{{{Z_L}}}{R} \Rightarrow \frac{{{Z_L}}}{R} = \tan \frac{\pi }{6} = \frac{1}{{\sqrt 3 }} \Leftrightarrow R = \sqrt 3 {Z_L}\)
Tổng trở của đoạn mạch:
\(Z = \sqrt {{R^2} + Z_L^2} = 2{Z_L} \Rightarrow {Z_L} = 20\Omega \)
Cảm kháng:
\({Z_L} = \omega L \Rightarrow L = \frac{{{Z_L}}}{\omega } = \frac{2}{{10\pi }} = 63,7mH\)
Vậy giá trị của L gần nhất với 65mH.
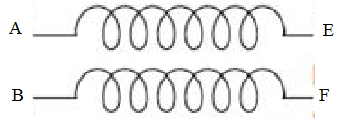
Một học sinh mắc mạch điện như hình vẽ. Đặt vào A và B điện áp xoay chiều
\(u = U\sqrt 2 \cos \left( {100\pi t } \right)\)
(U không đổi). Khi nối E, F với một ampe kế thì số chỉ của ampe kế là 3,8A. Khi nối E, F với một vôn kế thì số chỉ của vôn kế là 11,95V. Coi như hai cuộn dây thuần cảm và có hệ số tự cảm bằng nhau. Độ tự cảm cảu mỗi cuộn dây gần nhấu với giá trị nào sau đây?
-
A
5mH
-
B
20 mH
-
C
10 mH
-
D
15 mH
Đáp án của giáo viên lời giải hay : A
Khi mắc ampe kế vào E,F ta đo được cường độ dòng điện chạy trong mạch :
\(I = \frac{U}{{2{Z_L}}}\)
Khi mắc Vôn kế vào E, F thì ta đo được hiệu điện thế giữa hai điểm E, F tức là A, B (vì vôn kế lý tưởng và mạch thuần cảm).
Vậy là U = 11,95 V.
Cảm kháng:
\({Z_L} = \omega .L\)
Khi mắc ampe kế vào E,F ta đo được cường độ dòng điện chạy trong mạch :
\(I = \frac{U}{{2{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{2I}}\)
Khi mắc Vôn kế vào E, F thì ta đo được hiệu điện thế giữa hai điểm E, F tức là A, B (vì vôn kế lý tưởng và mạch thuần cảm). Vậy là U = 11,95V.
Lại có :
\(I = \frac{U}{{2{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{2I}} = \frac{{11,95}}{{2.3,8}} = 1,{572_{}}\Omega \)
Từ công thức tính cảm kháng ta có :
\(L = \frac{{{Z_L}}}{\omega } = \frac{{1,572}}{{100\pi }} = {5.10^{ - 3}}H = 5mH\)
Đặt vào hai đầu cuộn thuần cảm với độ tự cảm \(L = \frac{1}{\pi }H\) một hiệu điện thế xoay chiều \(u = {U_0}.\cos 100\pi t\left( V \right).\)Tại thời điểm t1có \({u_1} = 200V,{i_1}\; = 2A\); tại thời điểm t2có \({u_2} = 200\sqrt 2 V,{i_2} = 0\). Biểu thức của hiệu điện thế và dòng điện trong mạch là
-
A
\(u = 200\sqrt 2 .\cos 100\pi t(V);i = 2\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{2}} \right)\left( A \right)\)
-
B
\(u = 200\sqrt 2 .\cos 100\pi t(V);i = 2\cos \left( {100\pi t} \right)\left( A \right)\)
-
C
\(u = 200\sqrt 2 .\cos 100t(V);i = 2\sqrt 2 \cos \left( {100t} \right)\left( A \right)\)
-
D
\(u = 200.\cos 100\pi t(V);i = 2\cos \left( {100\pi t} \right)\left( A \right)\)
Đáp án của giáo viên lời giải hay : A
Đoạn mạch xoay chiều chỉ chứa cuộn cảm thuần thì:
+ Điện áp và cường độ dòng điện vuông pha với nhau. Ta có:
\(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\)
+ Cường độ dòng điện trễ pha \(\dfrac{\pi }{2}\) so với điện áp.
Đoạn mạch xoay chiều chỉ chứa cuộn cảm thuần thì điện áp và cường độ dòng điện vuông pha với nhau.
Ta có:
\(\begin{array}{l}
\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1 \Rightarrow \dfrac{{{{200}^2}}}{{U_0^2}} + \dfrac{2}{{I_0^2}} = \dfrac{{{{\left( {200\sqrt 2 } \right)}^2}}}{{U_0^2}} + \dfrac{0}{{I_0^2}} = 1\\
\left\{ \begin{array}{l}
{U_0} = 200\sqrt 2 V\\
{I_0} = 2\sqrt 2 A
\end{array} \right. \Rightarrow u = 200\sqrt 2 .\cos \left( {100\pi t} \right)V\\
\Rightarrow i = 2\sqrt 2 .\cos \left( {100\pi t - \dfrac{\pi }{2}} \right)A
\end{array}\)
Đặt điện áp xoay chiều \(u = {U_0}\cos \left( {100\pi t-\dfrac{\pi }{3}} \right)V\)vào hai đầu một cuộn cảm thuần có độ tự cảm \(L = \dfrac{1}{{2\pi }}H\). Ở thời điểm điện áp giữa hai đầu cuộn cảm là \(100\sqrt 2 {\rm{ }}V\)thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là
-
A
\(i = 2\sqrt 3 \cos \left( {100\pi t - \dfrac{{5\pi }}{6}} \right)A\)
-
B
\(i = 2\sqrt 3 \cos \left( {100\pi t + \dfrac{\pi }{6}} \right)A\)
-
C
\(i = 2\sqrt 2 \cos \left( {100\pi t + \dfrac{\pi }{6}} \right)A\)
-
D
\(i = 2\sqrt 2 \cos \left( {100\pi t - \dfrac{{5\pi }}{6}} \right)A\)
Đáp án của giáo viên lời giải hay : A
Mạch chỉ có cuộn cảm nên \(u \bot i \Rightarrow \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\)
Đối với cuộn cảm thuần: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_L} = {I_0}.{Z_L}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\)
Cảm kháng của cuộn cảm: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{2\pi }} = 50\Omega \)
Điện áp cực đại: \({U_0} = {I_0}{Z_C} = 50{I_0}\)
\(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1 \Leftrightarrow \dfrac{{{{\left( {100\sqrt 2 } \right)}^2}}}{{{{50}^2}.I_0^2}} + \dfrac{{{2^2}}}{{I_0^2}} = 1 \Rightarrow {I_0} = 2\sqrt 3 A\)
Mạch chỉ có cuộn cảm thuần nên i trễ pha hơn u góc \(\dfrac{\pi }{2}\)
\( \Rightarrow {\varphi _i} = - \dfrac{\pi }{3} - \dfrac{\pi }{2} = - \dfrac{{5\pi }}{6}\)
Phương trình của i là: \(i = 2\sqrt 3 \cos \left( {100\pi t - \dfrac{{5\pi }}{6}} \right)A\)
Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm không đổi, tụ điện có điện dung C thay đổi. Khi C = C1 thì tần số dao động riêng của mạch là 6MHz và khi C = C2 thì tần số dao động riêng của mạch là 8MHz. Nếu C = 2C1 + 3C2 thì tần số dao động riêng của mạch là
-
A
3,12MHz
-
B
16,25MHz
-
C
4,8MHz
-
D
10MHz
Đáp án của giáo viên lời giải hay : A
Tần số dao động riêng của mạch LC là \(f=\frac{1}{2\pi \sqrt{LC}}\)
Tần số dao động riêng của mạch LC là \(f=\dfrac{1}{2\pi \sqrt{LC}}\)
Khi C = C1 thì \({{f}_{1}}=\dfrac{1}{2\pi \sqrt{L{{C}_{1}}}}={{6.10}^{6}}Hz\) (1)
Khi C = C2 thì \({{f}_{2}}=\dfrac{1}{2\pi \sqrt{L{{C}_{2}}}}={{8.10}^{6}}Hz\) (2)
Khi C = 2C1 + 3C2 thì \(f=\dfrac{1}{2\pi \sqrt{L(2{{C}_{1}}+3{{C}_{2}})}}\) (3)
Từ (1) và (2) ta được C1 = (16/9)C2
Thay vào (3) ta được :
\(f = \dfrac{1}{{2\pi \sqrt {L(2.\dfrac{{16}}{9}{C_2} + 3{C_2})} }} = \dfrac{1}{{2\pi \sqrt {\dfrac{{59}}{9}L{C_2}} }} = \sqrt {\dfrac{9}{{59}}} {f_2} = 3,{12.10^6}Hz\)
Đặt một điện áp xoay chiều có \(u = 120\sqrt 2 \cos 100\pi t\,V\) vào hai đầu một mạch điện gồm một điện trở R nối tiếp với một bóng đèn 100 V – 100 W. Muốn đèn sáng bình thường thì R có giá trị là bao nhiêu?
-
A
20 Ω.
-
B
100 Ω.
-
C
10 Ω.
-
D
120 Ω.
Đáp án của giáo viên lời giải hay : A
Chọn đáp án A
+ Dòng điện chạy trong mạch khi đèn sáng bình thường\(I = \frac{{{P_d}}}{{{U_d}}} = \frac{{100}}{{100}} = 1\,\,{\rm{A}}{\rm{.}}\)
\( \to \) Điện áp hiệu dụng ở hai đầu điện trở \({U_R} = U - {U_d} = 20\,\,V.\)
\( \to \)Giá trị của R là
\({\rm{R}} = \frac{{{U_R}}}{I} = \frac{{20}}{I} = 20\,\,\Omega .\)
Đặt điện áp xoay chiều có giá trị cực đại là \(220\sqrt 2 V\) vào hai đầu một tụ điện thì cường độ dòng điện trong cuộn cảm có biểu thức \(i = 5.\cos 100\pi t\,\,\left( A \right)\). Tại thời điểm điện áp có 220V và đang tăng thì cường độ dòng điện là:
-
A
\( - 2,5\sqrt 3 A\)
-
B
\(2,5\sqrt 3 A\)
-
C
\(2,5\sqrt 2 A\)
-
D
\( - 2,5\sqrt 2 A\)
Đáp án của giáo viên lời giải hay : C
Sử dụng VTLG
Mạch điện chỉ chứa tụ điện có u trễ pha hơn i góc \(\dfrac{\pi }{2}\)
Đối với đoạn mạch chỉ chứa tụ điện thì điện áp hai đầu mạch luôn trễ pha hơn so với dòng điện một góc \(\dfrac{\pi }{2}\)
Biểu diễn trên VTLG ta có:
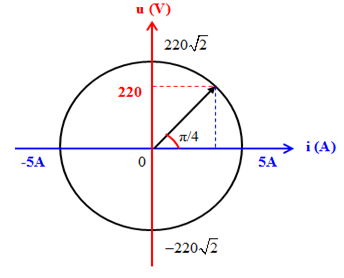
Từ VTLG ta thấy tại thời điểm u = 220V và đang tăng thì cường độ dòng điện:
\(i = {I_0}.\cos \dfrac{\pi }{4} = 5.\dfrac{{\sqrt 2 }}{2} = 2,5\sqrt 2 A\)
Cho cường độ dòng điện tức thời của đoạn mạch xoay chiều là \(i = 5\cos \left( {120\pi t - \dfrac{\pi }{3}} \right)A\). Khi đó
-
A
tần số của dòng điện là \(f = 120\;\,Hz\)
-
B
cường độ dòng điện cực đại là \({I_0} = 5\sqrt 2 \,A\)
-
C
pha dao động của dòng điện là \(\varphi = - \dfrac{\pi }{3}\;\,rad\)
-
D
cường độ dòng điện hiệu dụng là \(I = \dfrac{5}{{\sqrt 2 }}\;\,A\)
Đáp án của giáo viên lời giải hay : D
- Tần số của dòng điện là:
\(f = \frac{\omega }{{2\pi }} = \dfrac{{120\pi }}{{2\pi }} = 60Hz\) => A sai
- Cường độ dòng điện cực đại là:
\({I_0} = 5{\rm{A}}\) => B sai
- Pha dao động của dòng điện là \(\left( {120\pi t - \dfrac{\pi }{3}} \right)\) => C sai
- Cường độ dòng điện hiệu dụng: \(I = \dfrac{{{I_0}}}{{\sqrt 2 }} = \dfrac{5}{{\sqrt 2 }}A\) => D đúng
Đặt điện áp \(u = {U_0}\cos \left( {\omega t + \dfrac{\pi }{3}} \right)\) vào hai đầu cuộn cảm thuần có độ tự cảm \(L\) thì cường độ dòng điện qua cuộn cảm là
-
A
\(i = \dfrac{{{U_0}}}{{\omega L}}\cos \left( {\omega t - \dfrac{\pi }{6}} \right)\)
-
B
\(i = \dfrac{{{U_0}}}{{\omega L}}\cos \left( {\omega t + \dfrac{\pi }{6}} \right)\)
-
C
\(i = \dfrac{{{U_0}}}{{\omega L}}\cos \left( {\omega t - \dfrac{\pi }{3}} \right)\)
-
D
\(i = \dfrac{{{U_0}}}{{\omega L}}\cos \left( {\omega t + \dfrac{{5\pi }}{6}} \right)\)
Đáp án của giáo viên lời giải hay : A
Đối với đoạn mạch chỉ có cuộn cảm thuần:
\(\left\{ \begin{array}{l}u = {U_0}\cos \left( {\omega t + \varphi } \right)\\i = \dfrac{{{U_0}}}{{{Z_L}}}\cos \left( {\omega t + \varphi - \dfrac{\pi }{2}} \right)\end{array} \right.\)
Biểu thức của điện áp: \(u = {U_0}\cos \left( {\omega t + \dfrac{\pi }{3}} \right)\)
Biểu thức của cường độ dòng điện qua cuộn cảm thuần:
\(i = \dfrac{{{U_0}}}{{{Z_L}}}\cos \left( {\omega t + \dfrac{\pi }{3} - \dfrac{\pi }{2}} \right) = \dfrac{{{U_0}}}{{\omega L}}\cos \left( {\omega t - \dfrac{\pi }{6}} \right)\)
Điện áp \(u = 200co{\rm{s}}\left( {100\pi t + \frac{\pi }{2}} \right)\left( V \right)\) có giá trị hiệu dụng bằng
-
A
\(100\sqrt 2 V\).
-
B
\(200\sqrt 2 V\).
-
C
\(200V\).
-
D
\(100V\).
Đáp án của giáo viên lời giải hay : A
Biểu thức điện áp: \(u = {U_0}co{\rm{s}}\left( {\omega t + \varphi } \right)\)
Điện áp hiệu dụng: \(U = \dfrac{{{U_0}}}{{\sqrt 2 }}\)
Điện áp hiệu dụng: \(U = \dfrac{{{U_0}}}{{\sqrt 2 }} = \dfrac{{200}}{{\sqrt 2 }} = 100\sqrt 2 V\)
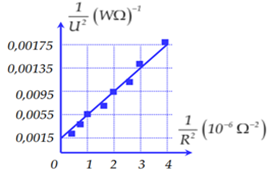
Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp \(u = {U_0}.cos\omega t\) (U0 không đổi, \(\omega = 314rad/s\)) vào hai đầu một đoạn mạch gồm tụ điện có điện dung C mắc nối tiếp với biến trở R. Biết \(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2{\omega ^2}{C^2}}}.\dfrac{1}{{{R^2}}}\); trong đó điện áp U giữa hai đầu R được đo bằng đồng hồ đo điện đa năng hiện số. Dựa vào kết quả thực nghiệm đo được trên hình vẽ, học sinh này tính được giá trị của C là:
-
A
\(5,{20.10^{ - 6}}F\)
-
B
\(1,{95.10^{ - 4}}F\)
-
C
\(1,{95.10^{ - 3}}F\)
-
D
\(5,{20.10^{ - 3}}F\)
Đáp án của giáo viên lời giải hay : B
Sử dụng các vị trí tại \(\dfrac{1}{{{R^2}}} = 1\) thì \(\dfrac{1}{{{U^2}}} = 0,0055\) và tại \(\dfrac{1}{{{R^2}}} = 2\) thì \(\dfrac{1}{{{U^2}}} = 0,0095\) ta tìm được C.
+ Tại: \(\dfrac{1}{{{R^2}}} = {10^{ - 6}}\) thì \(\dfrac{1}{{{U^2}}} = 0,0055\) ta có:
\(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}.\dfrac{1}{{{R^2}}} \Leftrightarrow 0,0055 = \dfrac{2}{{U_0^2}} + \dfrac{{{{2.10}^{ - 6}}}}{{U_0^2.{\omega ^2}.{C^2}}}\)
+ Tại: \(\dfrac{1}{{{R^2}}} = {2.10^{ - 6}}\) thì \(\dfrac{1}{{{U^2}}} = 0,0095\)ta có:
\(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}.\dfrac{1}{{{R^2}}} \Leftrightarrow 0,0095 = \dfrac{2}{{U_0^2}} + \dfrac{{{{4.10}^{ - 6}}}}{{U_0^2.{\omega ^2}.{C^2}}}\)
Ta được hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{0,0055 = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}{{.10}^{ - 6}}}\\{0,0095 = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}{{.2.10}^{ - 6}}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0,0055 = \dfrac{2}{{U_0^2}}.\left( {1 + \dfrac{1}{{3,{{14}^2}.{C^2}}}{{.10}^{ - 6}}} \right){\mkern 1mu} \,\,\,{\mkern 1mu} \left( 1 \right)}\\{0,0095 = \dfrac{2}{{U_0^2}}\left( {1 + \dfrac{1}{{3,{{14}^2}.{C^2}}}{{.2.10}^{ - 6}}} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)
Lấy (2) chia (1) ta được: \(C = 1,{95.10^{ - 4}}F\)
