Điện năng được truyền từ đường dây điện một pha có điện áp hiệu dụng ổn định \(220{\rm{ }}V\)vào nhà một hộ dân bằng đường dây tải điện có chất lượng kém. Trong nhà của hộ dân này, dùng một máy biến áp lí tưởng để duy trì điện áp hiệu dụng ở đầu ra luôn là \(220{\rm{ }}V\)(gọi là máy ổn áp). Máy ổn áp này chỉ hoạt động khi điện áp hiệu dụng ở đầu vào lớn hơn \(110{\rm{ }}V\). Tính toán cho thấy, nếu công suất sử dụng điện trong nhà là \(1,1{\rm{ }}kW\) thì tỉ số giữa điện áp hiệu dụng ở đầu ra và điện áp hiệu dụng ở đầu vào (tỉ số tăng áp) của máy ổn áp là\(1,1\) . Coi điện áp và cường độ dòng điện luôn cùng pha. Nếu công suất sử dụng điện trong nhà là \(2,2kW\) thì tỉ số tăng áp của máy ổn áp bằng:
-
A
\(1,55\)
-
B
\(2,20\)
-
C
$4,78$
-
D
\(1,26\)
Đáp án của giáo viên lời giải hay : D
- Sử dụng lí thuyết về truyền tải điện năng đi xa
- Sử dụng công thức của máy biến áp
Gọi điện áp từ dây điện là \({U_0}\) , điện áp đầu vào và đầu ra máy ổn áp lần lượt là \({U_1}\) và \({U_2}\).
Theo đề bài ta có: \({U_0} = {\text{ }}{U_2} = 220\left( V \right)\) và không thay đổi.
Công suất trong nhà là công suất đầu ra ổn áp, hơn nữa do máy ổn áp lí tưởng nên \({P_1} = {\rm{ }}{P_2} = {\rm{ }}{P_{nha}}\)
Ta có \({P_{nha}} = {\rm{ }}{P_1} = {\rm{ }}{U_1}I{\rm{ }} = \dfrac{{{U_2}I}}{k} = \dfrac{{220I}}{k}\) trong đó \(I\) là dòng điện chạy trên dây tải điện
Mặt khác \(I = \dfrac{{{U_0} - {U_1}}}{R} = \dfrac{{200}}{R} = \dfrac{{220 - \dfrac{{200}}{R}}}{R} = \dfrac{{220(k - 1)}}{{kR}}\) nên thay vào ta được
\({P_{nha}} = \dfrac{{{{220}^2}(k - 1)}}{{{k^2}R}}\) (Với $R$ là điện trở dây tải điện có giá trị không đổi)
Khi \({P_{nha}} = 1,1{\rm{ }}kW\) thì \(k{\rm{ }} = {\rm{ }}{k_1} = 1,1\) và khi thì \(k{\rm{ }} = {\rm{ }}{k_2}\) ta có tỷ số:
$\begin{array}{l}\dfrac{{{k_2} - 1}}{{{k_1} - 1}}.\dfrac{{k_1^2}}{{k_2^2}} = 2 \Leftrightarrow \dfrac{{{k_2} - 1}}{{k_2^2}} = \dfrac{{20}}{{121}}\\ \Leftrightarrow 20k_2^2 - 121{k_2} + 121 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{k_2} = 4,78\\{k_2} = 1,26\end{array} \right.\end{array}$
Bởi \({U_1} = \dfrac{{220}}{k} > 110(V) = > k < 2\)
=> Giá trị \({k_2} = {\rm{ }}4,78\) bị loại
Đặt điện áp xoay chiều $u{\rm{ }} = {\rm{ }}{U_0}cos\omega t$ (${U_0}$ và $\omega $ có giá trị dương, không đổi) vào hai đầu đoạn mạch AB như hình bên, trong đó tụ điện có điện dung C thay đổi được. Biết $R{\rm{ }} = {\rm{ }}5r$, cảm kháng của cuộn dây ${Z_L} = {\rm{ }}4r$ và $CL{\omega ^2} > {\rm{ }}1$. Khi $C{\rm{ }} = {\rm{ }}{C_0}$ và khi $C{\rm{ }} = {\rm{ }}0,5{C_0}$ thì điện áp giữa hai đầu M, B có biểu thức tương ứng là ${u_1} = {\rm{ }}{U_{01}}cos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)$ và ${u_2} = {\rm{ }}{U_{02}}cos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)$ (${U_{01}}$ và ${U_{02}}$ có giá trị dương). Giá trị của $\varphi $ là:
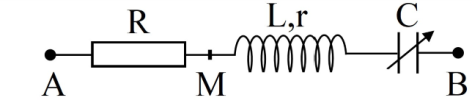
-
A
$0,47{\rm{ }}rad$
-
B
$0,62{\rm{ }}rad$
-
C
$1,05{\rm{ }}rad$
-
D
$0,79{\rm{ }}rad$
Đáp án của giáo viên lời giải hay : D
+ Sử dụng công thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Vận dụng các công thức lượng giác
Ta có:
$\varphi = {\tan ^{ - 1}}\left( {\dfrac{{{Z_L} - {Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\dfrac{{{Z_L} - {Z_C}}}{{R + r}}} \right)$(1);
theo bài ta có: ${\tan ^{ - 1}}\left( {\dfrac{{{Z_L} - {Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\dfrac{{{Z_L} - {Z_C}}}{{R + r}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{{Z_L} - 2{Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\dfrac{{{Z_L} - 2{Z_C}}}{{R + r}}} \right)$
${\tan ^{ - 1}}\left( {\dfrac{{4r - {Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\dfrac{{4r - {Z_C}}}{{6r}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{4r - 2{Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\dfrac{{4r - 2{Z_C}}}{{6r}}} \right)$
$ = > {Z_C} = r$ ; thay vào (1) ta tìm được $\varphi = 0,785rad$
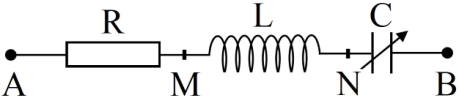
Đặt điện áp \({u_{AB}} = {\rm{ }}30cos100\pi t{\rm{ }}\left( V \right)\) vào hai đầu đoạn mạch \(AB\) như hình bên, trong đó cuộn cảm thuần có độ tự cảm \(L\) và tụ điện có điện dung \(C\) thay đổi được. Khi \(C{\rm{ }} = {\rm{ }}{C_0}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch \(MN\) đạt giá trị cực đại và điện áp hiệu dụng giữa hai đầu đoạn mạch \(AN\) là \(30\sqrt 2 V\). Khi \(C = 0,5{C_0}\) thì biểu thức điện áp giữa hai đầu cuộn cảm là:
-
A
\({u_{MN}} = 15\sqrt 3 {\rm{cos}}\left( {100\pi t + \dfrac{{5\pi }}{6}} \right)V\)
-
B
\({u_{MN}} = 15\sqrt 3 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{3}} \right)V\)
-
C
\({u_{MN}} = 30\sqrt 3 {\rm{cos}}\left( {100\pi t + \dfrac{{5\pi }}{6}} \right)V\)
-
D
\({u_{MN}} = 30\sqrt 3 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{3}} \right)V\)
Đáp án của giáo viên lời giải hay : A
+ Vận dụng các dạng bài C biến thiên
+ Sử dụng biểu thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Viết phương trình điện áp
Khi \(C = {C_o}\): \({U_{MN}}\) đạt cực đại, \(I = {I_{max}}\) ta có \(Z = R\) và \({Z_L} = {Z_{Co}}\) ; \({U_{AN}} = 30\sqrt 2 = \dfrac{{15\sqrt 2 }}{R}\sqrt {{R^2} + Z_L^2} \to {Z_L} = R.\sqrt 3 \)
Khi \(C = 0,5{C_o}\) thì \({Z_C} = 2{Z_L} = 2R\sqrt 3 \); góc lệch pha giữa \(u\) và \(i\):
\(\tan \varphi = \dfrac{{R\sqrt 3 - 2.R\sqrt 3 }}{R} = - \sqrt 3 \to \varphi = - \dfrac{\pi }{3}\)
=> Độ lệch pha của $u_L$ so với $i$ là:
\({\varphi _{uL}} = \dfrac{\pi }{3} + \dfrac{\pi }{2} = \dfrac{{5\pi }}{6}\)
$\begin{array}{l} \to {u_L} = \dfrac{{30R\sqrt 3 }}{{\sqrt {{R^2} + 3{R^2}} }}c{\rm{os}}\left( {{\rm{100}}\pi {\rm{t + }}\dfrac{{5\pi }}{{\rm{6}}}} \right)(V)\\ = 15\sqrt 3 c{\rm{os}}\left( {{\rm{100}}\pi {\rm{t + }}\dfrac{{5\pi }}{{\rm{6}}}} \right)(V)\end{array}$
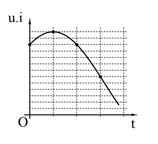
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có \(R,{\rm{ }}L,{\rm{ }}C\) mắc nối tiếp thì dòng điện trong đoạn mạch có cường độ \(i\). Hình bên là một phần đồ thị biểu diễn sự phụ thuộc của tích \(u.i\) theo thời gian \(t\). Hệ số công suất của đoạn mạch là:
-
A
\(0,625\)
-
B
\(0,866\)
-
C
\(0,500\)
-
D
\(0,707\)
Đáp án của giáo viên lời giải hay : A
+ Đọc đồ thị p – t
+ Sử dụng biểu thức u, i: \(\left\{ \begin{array}{l}u = {U_0}{\rm{cos}}\left( {\omega t + \varphi } \right)\\i = {I_0}{\rm{cos}}\left( {\omega t + \varphi } \right)\end{array} \right.\)
+ Sử dụng biểu thức tính góc của hệ số công suất: \(\varphi = {\varphi _u} - {\varphi _i}\)
+ Vận dụng biểu thức tính công suất: \(p = ui\)
+ Vận dụng các công thức lượng giác
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}u = {U_0}\cos (\omega t + {\varphi _u})\\i = {I_0}\cos (\omega t + {\varphi _i})\end{array} \right.\\\left\{ \begin{array}{l}{\varphi _u} + {\varphi _i} = x\\{\varphi _u} - {\varphi _i} = \varphi \end{array} \right.\end{array}\)
\(p = ui = UI(\cos (2\omega t + x) + \cos \varphi )\)
Ta có:
\(13{\rm{ }} = UI\left( {1{\rm{ }} + {\rm{ }}cos\varphi } \right)\) (1)
và \(2\omega {t_0} + x{\text{ }} = {\text{ }}2\pi {\text{ }} + {\text{ }}k2\pi \)
\(t{\text{ }} = {\text{ }}0,p{\text{ }} = {\text{ }}11{\text{ }} = {\text{ }}UI\left[ {cosx{\text{ }} + cos\varphi } \right]\) (2)
\(\begin{array}{l}t = 3{t_0},p = 6 = UI\left[ {cos\left( {2\omega .3{t_0} + x} \right) + cos\varphi } \right]\\ = UI\left[ {cos\left( {6\pi - 2x} \right) + cos\varphi } \right]\\ = UI\left[ {cos\left( { - 2x} \right){\rm{ }} + {\rm{ }}cos\varphi } \right]{\rm{ }}\left( 3 \right)\end{array}\)
Lấy (1) chia (2) ta được: \(cos\varphi {\rm{ }} = {\rm{ }}5,5 - 6,5cosx\)
Lấy (1) chia (3) ta được: \(\dfrac{{13}}{6} = \dfrac{{1{\rm{ }} + {\rm{ }}cos\varphi }}{{ - cos\left( {2x} \right){\rm{ }} + {\rm{ }}cos\varphi }} = \dfrac{{1 + 5,5 - 6,5cosx}}{{2.co{s^2}x{\rm{ }} - 1{\rm{ }} + 5,5{\rm{ }} - 6,5cosx}}\)
Suy ra \(\left[ \begin{array}{l}cosx = 0,75\\\cos x = 1\left( {loai} \right)\end{array} \right.\)
Với \(\cos x = 0,75 \to cos\varphi = 0,625\)
Điện năng được truyền từ một nhà máy phát điện gồm \(8\) tổ máy đến nơi tiêu thụ bằng đường dây tải điện một pha. Giờ cao điểm cần cả \(8\) tổ máy hoạt động, hiệu suất truyền tải đạt \(70\% \). Coi điện áp hiệu dụng ở nhà máy không đổi, hệ số công suất của mạch điện bằng \(1\), công suất phát điện của các tổ máy khi hoạt động là không đổi và như nhau. Khi công suất tiêu thụ điện ở nơi tiêu thụ giảm còn \(72,5\% \) so với giờ cao điểm thì cần bao nhiêu tổ máy hoạt động?
-
A
5
-
B
6
-
C
4
-
D
7
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính công suất hao phí khi truyền tải điện năng: \(\Delta P = \dfrac{{{P^2}R}}{{{{\rm{U}}^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\)
Ta có:
\(\Delta {P_1} = 0,30{P_1} = \dfrac{{R.P_1^2}}{{{U^2}}} \to \dfrac{R}{{{U^2}}} = \dfrac{{0,30}}{{{P_1}}}\);
\(\Delta {P_2} = \dfrac{{R.P_2^2}}{{{U^2}}} = \dfrac{{0,30.P_2^2}}{{{P_1}}}\);
\({P_2} = \dfrac{{0,30}}{{{P_1}}}.P_2^2 + \dfrac{{203}}{{400}}{P_1} \to {P_2} = 0,625{P_1} = 0,625.8{P_0} = 5{P_0}\)
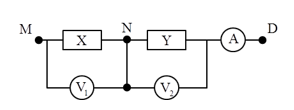
Cho mạch điện như hình vẽ: \(X,{\rm{ }}Y\) là hai hộp, mỗi hộp chỉ chứa $2$ trong $3$ phần tử: điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Ampe kế có điện trở rất nhỏ, các vôn kế có điện trở rất lớn. Các vôn kế và ampe kế đo được cả dòng điện xoay chiều và một chiều. Ban đầu mắc hai điểm $N, D$ vào hai cực của một nguồn điện không đổi thì \({V_2}\) chỉ \(45{\rm{ }}V\), ampe kế chỉ \(1,5{\rm{ }}A\). Sau đó mắc \(M,{\rm{ }}D\) vào nguồn điện xoay chiều có điện áp \(u{\rm{ }} = {\rm{ }}120cos100\pi t{\rm{ }}V\) thì ampe kế chỉ \(1{\rm{ }}A\), hai vôn kế chỉ cùng một giá trị và $u_{MN}$ lệch pha $0,5π $ so với $u_{ND}$. Khi thay tụ $C$ trong mạch bằng tụ $C’$ thì số chỉ vôn kế \({V_1}\) lớn nhất \({U_{1max}}\) . Giá trị \({U_{1max}}\) gần giá trị nào nhất sau đây?
-
A
$90 V$
-
B
$75 V$
-
C
$120 V$
-
D
$105 V$
Đáp án của giáo viên lời giải hay : B
+ Sử dụng phương pháp giải bài toán hộp đen
+ Áp dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Áp dụng biểu thức: \(Z = \dfrac{U}{I}\)
+ Vận dụng biểu thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Khi mắc vào hai cực $ND$ một điện áp không đổi $ \to $ có dòng trong mạch với cường độ $I = 1,5{\mkern 1mu} {\mkern 1mu} {\rm{A}} \to $ $ND$ không thể chứa tụ (tụ không cho dòng không đổi đi qua) và ${{\rm{R}}_Y} = \dfrac{{40}}{{1,5}} = 30{\mkern 1mu} {\mkern 1mu} \Omega $
+ Mắc vào hai đầu đoạn mạch $MB$ một điện áp xoay chiều thì ${u_{ND}}$ sớm pha hơn ${u_{MN}}$ một góc \(0,5\pi {\text{}} \to \) X chứa điện trở ${{\rm{R}}_X}$ và tụ điện $C$, $Y$ chứa cuộn dây $L$ và điện trở ${{\rm{R}}_Y}$ .
$ \to $ với ${V_1} = {V_2} \to {U_X} = {U_Y} = 60{\mkern 1mu} {\mkern 1mu} V \to {Z_X} = {Z_Y} = 60{\mkern 1mu} {\mkern 1mu} \Omega $
+ Cảm kháng của cuộn dây ${{\text{Z}}_L} = \sqrt {Z_Y^2 - R_Y^2} {\text{}} = \sqrt {{{60}^2} - {{30}^2}} {\text{}} = 30\sqrt 3 {\mkern 1mu} {\mkern 1mu} \Omega $ .
+ Với ${u_{MN}}$ sớm pha $0,5\pi $ so với ${u_{N{\rm{D}}}}$ và $\tan {\varphi _Y} = \dfrac{{{Z_L}}}{{{R_Y}}} = \dfrac{{30\sqrt 3 }}{{30}} = \sqrt 3 {\text{}} \to {\varphi _Y} = {60^0}$
$ \to {\varphi _X} = {30^0}$
$ \to \left\{ {\begin{array}{*{20}{l}}{{R_X} = 30\sqrt 3 \Omega }\\{{Z_C} = 30\Omega }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} $ .
+ Điện áp hiệu dụng hai đầu $MN$: ${V_1} = {U_{MN}} = \dfrac{{U\sqrt {R_X^2 + Z_C^2} }}{{\sqrt {{{\left( {{R_X} + {R_Y}} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{60\sqrt 2 \sqrt {{{\left( {30\sqrt 3 } \right)}^2} + Z_C^2} }}{{\sqrt {{{\left( {30\sqrt 3 {\text{}} + 30} \right)}^2} + {{\left( {30\sqrt 3 - {Z_C}} \right)}^2}} }}$
+ Sử dụng bảng tính Mode $ \to $ $7$ trên Casio ta tìm được ${V_{1\max }}$ có giá trị lân cận \(75V\)
Đặt điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\) (\(U\) không đổi, \(\omega \) thay đổi) vào hai đầu đoạn mạch gồm: một điện trở thuần \(R\), một cuộn cảm thuần có độ tự cảm \(L\), một tụ điện có điện \(C\) mắc nối tiếp \(\left( {2L > C{R^2}} \right)\). Khi \(\omega = 100\pi \left( {rad/s} \right)\) thì điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại. Khi \(\omega = 200\pi \left( {rad/s} \right)\) thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cức đại. Giá trị điện áp hiệu dụng cực đại giữa hai đầu cuộn cảm là:
-
A
\(U\sqrt 3 \)
-
B
\(\dfrac{{2U}}{{\sqrt 3 }}\)
-
C
\(U\sqrt 2 \)
-
D
\(\dfrac{{2U}}{{\sqrt 2 }}\)
Đáp án của giáo viên lời giải hay : B
Bài toán điều kiện cực trị khi tần số thay đổi
+ \(f\) biến thiên để \({U_{{L_{max}}}}\) : \({U_{L\max }} = \dfrac{{2.U.L}}{{R.\sqrt {4LC - {R^2}.{C^2}} }}\), \({\omega _L} = \dfrac{1}{C}\sqrt {\dfrac{2}{{\dfrac{{2L}}{C} - {R^2}}}} {\rm{}}\)
+ \(f\) biến thiên để \({U_{{C_{max}}}}\) : \({U_{C\max }} = \dfrac{{2.U.L}}{{R.\sqrt {4LC - {R^2}.{C^2}} }}\), \({\omega _C} = \dfrac{1}{L}\sqrt {\frac{{2L - {R^2}.C}}{2}} {\rm{}}\)
Điều kiện cực trị khi tần số thay đổi.
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có: \({U_{L\max }} = \dfrac{{2.U.L}}{{R.\sqrt {4LC - {R^2}.{C^2}} }} \Leftrightarrow {\omega _L} = \dfrac{1}{C}.\sqrt {\dfrac{2}{{\dfrac{{2L}}{C} - {R^2}}}} {\rm{}} = 200\pi \)
Và điện áp trên tụ cực đại là:\({U_{C\max }} = \dfrac{{2.U.L}}{{R.\sqrt {4LC - {R^2}.{C^2}} }} \Leftrightarrow {\omega _C} = \dfrac{1}{L}.\sqrt {\dfrac{{2L - {R^2}.C}}{2}} {\rm{}} = 100\pi \)
Ta thấy: \({U_{L\max }} = {U_{C\max }} = \dfrac{U}{{\sqrt {1 - \dfrac{{\omega _C^2}}{{\omega _L^2}}} }} = \dfrac{U}{{\sqrt {1 - \dfrac{1}{4}} }} = \dfrac{{2.U}}{{\sqrt 3 }}V\)
Cho đoạn mạch xoay chiều $AB$ nối tiếp gồm: $AM$ chứa biến trở $R$, đoạn mạch $MN$ chứa $r$, đoạn $NP$ chứa cuộn cảm thuần, đoạn $PB$ chứa tụ điện có điện dung biến thiên. Ban đầu thay đổi tụ điện sao cho ${U_{AP}}$ không phụ thuộc vào biến trở $R$. Giữ nguyên giá trị điện dung đó và thay đổi biến trở. Khi${u_{AP}}$ lệch pha cực đại so với ${u_{AB}}$ thì ${U_{PB}} = {U_1}$ . Khi $\left( {{U_{AN}}.{U_{NP}}} \right)$ cực đại thì ${U_{AM}} = {U_2}$. Biết rằng ${U_1} = 2.(\sqrt 6 {\text{}} - \sqrt 3 ){U_2}$ . Độ lệch pha cực đại giữa ${u_{AP}}$ và ${u_{AB}}$ gần nhất với giá trị nào?
-
A
\(\dfrac{{5\pi }}{7}\)
-
B
\(\dfrac{{3\pi }}{7}\)
-
C
\(\dfrac{{6\pi }}{7}\)
-
D
\(\dfrac{{4\pi }}{7}\)
Đáp án của giáo viên lời giải hay : D
+ C biến thiên để \({U_{RL}}\) không phụ thuộc vào R: \({Z_C} = 2{Z_L}\)
+ Sử dụng giản đồ véc-tơ
+ Sử dụng định luật Ôm và các biến đổi toán học
Khi thay đổi \(C\) để \({U_{AP}}\) không phụ thuộc biến trở \(R\) Ta có:
+ Khi R thay đổi ta luôn có \(\Delta APB\) luôn là tam giác cân tại \(A\)
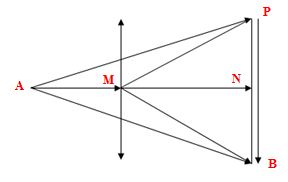
+ Ta thấy khi $R$ thay đổi, nếu ta di chuyển điểm $A \to M$ thì góc $2\varphi $ chính là độ lệch pha của ${U_{AP}}$ và ${U_{AB}}$ và nó càng lớn. Vậy độ lệch pha cực đại của ${U_{AP}}$ và ${U_{AB}}$ khi điểm $A$ trùng với điểm $M$ hay lúc đó $R = 0$.
Khi đó: ${U_1} = {U_{PB}} = \dfrac{U}{{{Z_1}}}.{Z_C} = \dfrac{U}{{\sqrt {{r^2} + Z_L^2} }}.2{Z_L}$
+ Khi $R = {R_0}$ : ${U_{AN}}.{U_{NP}} \le \dfrac{{U_{AN}^2 + U_{NP}^2}}{2} = \dfrac{{{U^2}}}{2}$
Vậy ${U_{AN}}.{U_{NP}}$ lớn nhất khi hay khi đó tam giác $APB$ là tam giác vuông cân.
Lúc này: ${U_2} = {U_{AM}} = \dfrac{U}{{\sqrt 2 }} - {U_r}$
Từ hình vẽ ta suy ra; $\left\{ \begin{gathered} {Z_L} = {\text{ }}R{\text{ }} + {\text{ }}r \hfill \\ {Z_2} = \sqrt 2 .(R + r) \hfill \\\end{gathered} \right.$
Nên : ${U_2} = \dfrac{U}{{\sqrt 2 }} - I.r = \dfrac{U}{{\sqrt 2 }} - \dfrac{U}{{{Z_2}}}.r = \dfrac{U}{{\sqrt 2 }} - \dfrac{U}{{\sqrt 2 .(R + r)}}.r \Rightarrow {U_2} = \dfrac{{U.({Z_L} - r)}}{{\sqrt 2 .{Z_L}}}$
Lại có, từ đề bài: ${U_1} = 2.(\sqrt 6 {\text{}} + \sqrt 3 ).{U_2}$
Nên ta có:
$\begin{array}{l}\dfrac{U}{{\sqrt {{r^2} + Z_L^2} }}.2.{Z_L} = 2.(\sqrt 6 + \sqrt 3 ).\dfrac{{U.({Z_L} - r)}}{{\sqrt 2 .{Z_L}}}\\ \Rightarrow \dfrac{{{Z_L}}}{{\sqrt {{r^2} + Z_L^2} }} = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}\dfrac{{{Z_L} - r}}{{{Z_L}}}\\Z_L^2 = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}.({Z_L} - r).\sqrt {{r^2} + Z_L^2} \Rightarrow {\left( {\dfrac{{{Z_L}}}{r}} \right)^2} = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}.\left( {\dfrac{{{Z_L}}}{r} - 1} \right).\sqrt {1 + {{\left( {\dfrac{{{Z_L}}}{r}} \right)}^2}} \end{array}$
Đặt $x = tan\varphi {\text{}} = \dfrac{{{Z_L}}}{r}$ ta có phương trình:
\(\begin{array}{l}{x^2} = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}\left( {x - 1} \right)\sqrt {1 + {x^2}} \\ \to x \approx 1,377\\ \to \varphi \approx {54^0}\\ \to 2\varphi \approx {108^0} \approx \dfrac{3}{5}\pi \end{array}\)
=> Gần với \(\dfrac{{4\pi }}{7}\) nhất
Một đoạn mạch \(AB\) gồm hai đoạn mạch \(AM\) và \(MB\) mắc nối tiếp. Đoạn mạch \(AM\) chỉ có biến trở \(R\), đoạn mạch \(MB\) gồm tụ \(C\) mắc nối tiếp với cuộn dây không thuần cảm có độ tự cảm \(L\), điện trở thuần \(r\). Đặt vào \(AB\) một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Điều chỉnh \(R\) đến giá trị \(80\Omega \) thì công suất tiêu thụ trên biến trở đạt cực đại, đồng thời tổng trở của đoạn mạch \(AB\) là số nguyên và chia hết cho \(40\). Khi đó hệ số công suất của đoạn mạch \(MB\) có giá trị là:
-
A
$0,8$
-
B
$0,25$
-
C
$0,75$
-
D
$0,125$
Đáp án của giáo viên lời giải hay : D
+ Dạng bài Mạch RLC có R biến thiên để \({P_{{R_{max}}}}\) , khi đó: \(R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính hệ số công suất: \({\rm{cos}}\varphi =\dfrac{R}{Z}\)
Điều chỉnh R đến giá trị \(80\Omega \) thì công suất tiêu thụ trên biến trở cực đại
\( \Rightarrow R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = 80\) (1)
Có tổng trở của đoạn mạch là số nguyên và chia hết cho \(40\)
\( \to {Z_{AB}} = 40n\) (n là số nguyên)
\( \Rightarrow {Z_{AB}} = \sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = 40n \Leftrightarrow {\left( {80 + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\) (2)
Từ (1) và (2) ta có: \(\left\{ \begin{array}{l}{r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {80^2}\\{\left( {80 + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {80^2}\\{80^2} + 160r + {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\end{array} \right. \Rightarrow r = 10{n^2} - 80\)
Hệ số công suất của đoạn MB là: \(c{\rm{os}}{\varphi _{MB}} = \dfrac{r}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{10{n^2} - 80}}{{80}}\)
Có: \(c{\rm{os}}{\varphi _{MB}} \le 1 \Leftrightarrow \dfrac{{10{n^2} - 80}}{{80}} \le 1 \Rightarrow n \le 4\)
+ Với \(n = 4 \to cos{\varphi _{MB}} = 1\)
+ Với \(n{\rm{ }} = {\rm{ }}3 \to c{\rm{os}}{\varphi _{MB}} = \dfrac{{{{10.3}^2} - 80}}{{80}} = 0,125\)
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi \(u = 120\sqrt 2 {\rm{cos100}}\pi {\rm{t}}\left( V \right)\) vào đoạn mạch \(AB\) gồm đoạn \(AM\)chỉ chứa điện trở \(R\), đoạn mạch \(MB\) chứa tụ điện có điện dung \(C\) thay đổi được mắc nối tiếp với một cuộn cảm thuần. Biết sau khi thay đổi \(C\) thì điện áp hiệu dụng hai đầu mạch \(MB\) tăng \(\sqrt 2 \) lần và dòng điện tức thời trong mạch trước và sau khi thay đổi \(C\) lệch pha nhau một góc \(\dfrac{{5\pi }}{{12}}\). Điện áp hiệu dụng hai đầu mạch \(AM\) khi chưa thay đổi \(C\) có giá trị bằng:
-
A
\(60\sqrt 3 V\)
-
B
\(60\sqrt 2 V\)
-
C
\(120{\rm{ }}V\)
-
D
\(60{\rm{ }}V\)
Đáp án của giáo viên lời giải hay : A
+ Vận dụng biểu thức tính độ lệch pha của i so với u
+ Vận dụng các công thức lượng giác
+ Vận dụng máy tính giải phương trình
Ta có \({\varphi _{i1}} - {\varphi _{12}} = \left( {{\varphi _u} - {\varphi _1}} \right) - \left( {{\varphi _u} - {\varphi _2}} \right) = {\varphi _2} - {\varphi _1} = \dfrac{{5\pi }}{{12}}\left( 1 \right)\)
(Giả sử trường hợp một mạch có tính dung kháng và trường hợp hai mạch có tính cảm kháng).
*Trước và sau khi thay đổi C ta có hai trường hợp, trong đó một trường hợp mạch có tính cảm kháng và một trường hợp mạch có tính dung kháng \(\left\{ \begin{array}{l}\sin {\varphi _1} = \dfrac{{{U_{1LC}}}}{U}\\\sin {\varphi _2} = \dfrac{{{U_{2LC}}}}{U}\end{array} \right. = > \left\{ \begin{array}{l}{\varphi _1} = - \arcsin \dfrac{{{U_{1LC}}}}{U} = - \arcsin \dfrac{{{U_{1LC}}}}{{120}}\\{\varphi _2} = \arcsin \dfrac{{{U_{2LC}}}}{U} = \arcsin \dfrac{{\sqrt 2 {U_{1LC}}}}{{120}}\end{array} \right.\)
Thế vào (1), ta được:
\(\begin{array}{l}\arcsin \dfrac{{\sqrt 2 {U_{1LC}}}}{{120}} + \arcsin \dfrac{{{U_{1LC}}}}{{120}} = \dfrac{{5\pi }}{{12}} \Rightarrow {U_{1LC}} = 60V\\ \Rightarrow {U_{1R}} = \sqrt {{U^2} - U_{1LC}^2} = \sqrt {{{120}^2} + {{60}^2}} = 60\sqrt 3 V\end{array}\)
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch nối tiếp gồm cuộn dây có điện trở \(R\), hệ số tự cảm \(L\) và tụ điện có điện dung \(C\) thay đổi được. Ban đầu \(C = {C_1}\), khi đó điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch, điện áp hai đầu cuộn dây có giá trị hiệu dụng là \(60{\rm{ }}V\) và nhanh pha hơn điện áp hai đầu đoạn mạch một góc \(\dfrac{\pi }{3}\) . Giảm dần điện dung của tụ đến giá trị \(C = {C_2}\) thì hiệu điện áp hiệu dụng hai đầu tụ điện và điện áp hiệu dụng hai đầu cuộn dây bằng \(10V\). Khi đó điện áp hiệu dụng hai đầu cuộn dây có giá trị gần nhất với giá trị nào sau đây?
-
A
\(45{\rm{ }}V\)
-
B
\(50{\rm{ }}V\)
-
C
\(30{\rm{ }}V\)
-
D
\(60{\rm{ }}V\)
Đáp án của giáo viên lời giải hay : B
+ Vẽ giản đồ véc-tơ
+ Sử dụng biểu thức tính \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{{U_L} - {U_C}}}{{{U_R}}}\)
+ Hiệu điện thế hiệu dụng của mạch: \({U^2} = U_R^2 + {\left( {{U_L} - {U_C}} \right)^2}\)
+ Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
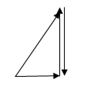
+ Khi \(C = {C_1}\) , \(u\) cùng pha với \(i\), trong mạch có cộng hưởng.
\({U_{AB}} = {U_R};{U_{LR}} = {\rm{ }}60V\)
\(\begin{array}{l}\tan \varphi = \frac{{{U_L}}}{{{U_R}}} = \tan {60^0} = \sqrt 3 \to {U_L} = \sqrt 3 {U_R}\\{U_{LR}} = \sqrt {U_L^2 + U_R^2} = 60\\ \to \left\{ \begin{array}{l}{U_L} = 30\sqrt 3 V\\{U_R} = 30V\end{array} \right.\end{array}\)
\(\dfrac{R}{{{Z_L}}} = \dfrac{{{U_R}}}{{{U_L}}} = \dfrac{1}{{\sqrt 3 }} \Rightarrow {Z_L} = \sqrt 3 R = {Z_{{C_1}}}\)
\({U_{AB}} = {U_R} = 30V\)
+ Khi\(C = {C_2}\) thì \({U_{{C_2}}} - {U_{LR'}} = 10V\)
Đặt \({U_{LR'}} = a \to {U_{{C_2}}} = a + 10\) Biết \({U_{AB}} = 30V\), ta có : \(\begin{array}{l}U_{_R}^2 + {\left( {{U_L}^\prime - {U_{{C_2}}}} \right)^2} = {30^2} \Leftrightarrow U_{_R}^2 + U_{_L}^2 + U_{{C_2}}^2 - 2.{U_L}^\prime .{U_{{C_2}}} = 900\\ \Leftrightarrow U_{_{LR}}^2 - 2.{U_L}^\prime .{U_{{C_2}}} + {U^2}_{{C_2}} = 900(*)\end{array}\)
Mặt khác, vì \({Z_L} = \sqrt 3 R \Rightarrow {U_L}^\prime = \sqrt 3 {U_R}^\prime \)
\(\begin{array}{l}{U_{LR'}} = \sqrt {{U_R}{'^2} + {U_L}{'^2}} = 2{U_R}' = \dfrac{2}{{\sqrt 3 }}{U_L}'\\ \Rightarrow {U_L}^\prime = \dfrac{{\sqrt 3 }}{2}{U_{LR}}^\prime \end{array}\)
Thay \({U_{LR'}} = a;{U_{{C_2}}} = a + 10\) vào biểu thức (*) ta được : \(\begin{array}{l}{a^2} + {(a + 10)^2} - 2.(a + 10).\dfrac{{\sqrt 3 }}{2}a = 900\\ \Rightarrow (2 - \sqrt 3 ){a^2} + (20 - 10\sqrt 3 )a - 800 = 0 \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 49,86V\\{a_2} = - 59,86V\end{array} \right.\end{array}\)
Chọn đáp án gần giá trị \(a{\rm{ = }}49,86V = 50V\)
Đặt điện áp \(u = {U_0}cos100\pi t\) vào hai đầu đoạn mạch \(AB\) theo thứ tự gồm \(R\), cuộn dây thuần cảm \(L\) và tụ \(C\) nối tiếp. Gọi \(M\) là điểm nối giữa \(R\) và \(L\). Điện áp tức thời của đoạn mạch \(AM\) (chứa R) và \(MB\) (chứa L và C) tại thời điểm \({t_1}\) là \({u_{AM}} = 60V;{u_{MB}} = 15\sqrt 7 V\) và tại thời điểm \({t_2}\) là \({u_{AM}} = 40\sqrt 3 V;{u_{MB}} = 30V\). Giá trị của \({U_0}\) bằng:
-
A
$100V$
-
B
\(50\sqrt 2 V\)
-
C
\(25\sqrt 2 V\)
-
D
\(100\sqrt 2 V\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ thức vuông pha
Đoạn mạch \(\) chứa \(R\), đoạn \(\) chứa \(L\) và \({\rm{?u}}\)
=>\({u_{AM}}\) và \({u_{MB}}\) vuông pha với nhau
=> Ở mọi thời điểm ta có:
\(\dfrac{{u_R^2}}{{U_{0R}^2}} + \dfrac{{u_{LC}^2}}{{U_{0LC}^2}} = 1 \Rightarrow \left\{ \begin{array}{l}\dfrac{{{{60}^2}}}{{U_{0R}^2}} + \dfrac{{{{\left( {15\sqrt 7 } \right)}^2}}}{{U_{0LC}^2}} = 1\\\dfrac{{{{\left( {40\sqrt 3 } \right)}^2}}}{{U_{0R}^2}} + \dfrac{{{{30}^2}}}{{U_{0LC}^2}} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{{U_{0R}^2}} = \dfrac{1}{{6400}}\\\dfrac{1}{{U_{0LC}^2}} = \dfrac{1}{{3600}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}U_{0R}^2 = 6400\\U_{0LC}^2 = 3600\end{array} \right.\)
=> Điện áp cực đại: \({U_0} = \sqrt {U_{0R}^2 + U_{0LC}^2} {\rm{}} = \sqrt {6400 + 3600} {\rm{}} = 100V\)
Đặt một điện áp xoay chiều \(u = U\sqrt 2 c{\rm{os}}\omega t(V)\) , trong đó \(U\) không đổi, \(\omega \) thay đổi được vào một đoạn mạch gồm có điện trở \(R\), tụ điện và cuộn cảm thuần có hệ số tự cảm \(L = \dfrac{{1,6}}{\pi }H\) mắc nối tiếp. Khi \(\omega = {\omega _0}\) thì công suất trên đoạn mạch đạt cực đại và bằng \(732W\). Khi \(\omega = {\omega _1}\) hoặc \(\omega = {\omega _2}\) thì công suất tiêu thụ trên đoạn mạch bằng nhau và bằng \(300W\). Biết \({\omega _1} - {\omega _2} = 120\pi \left( {rad/s} \right)\). Giá trị của \(R\) bằng:
-
A
\(240\Omega \)
-
B
\(133,3\Omega \)
-
C
\(160\Omega \)
-
D
\(400\Omega \)
Đáp án của giáo viên lời giải hay : C
Bài toán mạch điện R, L, C mắc nối tiếp có ω thay đổi
+ Khi \(\omega {\rm{ }} = {\rm{ }}{\omega _0}\) công suất trên mạch đạt cực đại: \(\) \(\omega _0^2 = \dfrac{1}{{LC}}\) , \({P_{m{\rm{ax}}}} = \dfrac{{{U^2}}}{R} = 732 \Rightarrow {U^2} = 732R(*)\)
+ Khi \(\omega = {\omega _1}\) và \(\omega = {\omega _2}\) ; \({\omega _1}-{\omega _2} = 120\pi \) thì công suất tiêu thụ trên đoạn mạch bằng nhau :
$\begin{array}{l}{P_1} = {P_2} = P = 300{\rm{W}}\\ \Leftrightarrow \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}}} = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}}\\ \Rightarrow {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}$
+ Ta có :
$\begin{array}{l}{Z_{L1}} - {Z_{C1}} = {\omega _1}L - \dfrac{1}{{{\omega _1}{C_1}}} = {\omega _1}L - \dfrac{1}{{\dfrac{{\omega _0^2}}{{{\omega _2}}}C}}\\ \leftrightarrow {\omega _1}L - \dfrac{{{\omega _2}}}{{\omega _0^2C}} = {\omega _1}L - \dfrac{{{\omega _2}}}{{\dfrac{1}{{LC}}C}}\\ = {\omega _1}L - {\omega _2}L = \left( {{\omega _1} - {\omega _2}} \right)L = 120\pi \dfrac{{1,6}}{\pi } = 192\\ \Rightarrow {Z_{L1}} - {Z_{C1}} = 192(**)\end{array}$
+ Công suất tiêu thụ : \(P = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}}} = 300 \Rightarrow 300{R^2} + 300{\left( {{Z_{L1}} - {Z_{C1}}} \right)^2} = {U^2}R(***)\)
Từ (*) ; (**) ; (***) ta suy ra: \(300{R^2} + {300.192^2} = 732{R^2} \Rightarrow R = 160\Omega \)
Đoạn mạch $AB$ được mắc nối tiếp theo thứ tự, cuộn dây với hệ số tự cảm $L = \dfrac{2}{{5\pi }}H$ , biến trở $R$ và tụ điện có điện dung $C = \dfrac{{{{10}^{ - 2}}}}{{25\pi }}F$. Điểm $M$ là điểm nối giữa $R$ và $C$. Nếu mắc vào hai đầu $A, M$ một ắc quy có suất điện động $12V$ và điện trở trong $4\Omega $ điều chỉnh $R = {R_1}$ thì có dòng điện cường độ $0,1875A$. Mắc vào $AB$ một hiệu điện thế $u = 120\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)\left( V \right)$ rồi điều chỉnh $R = {R_2}$ thì công suất tiêu thụ trên biến trở đạt cực đại bằng $160W$. Tỷ số ${R_1}:{R_2}$ là:
-
A
$1,6$
-
B
$0,25$
-
C
$0,125$
-
D
$0,45$
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Giả sử cuộn dây thuần cảm:
Ta có, khi \(R{\rm{ }} = {\rm{ }}{R_2}\) công suất tiêu thụ trên biến trở cực đại.
Khi đó ta có: \({R_2} = \left| {{Z_L} - {Z_C}} \right| = 40 - 25 = 15W\)
Mặt khác: \({P_{{R_2}}} = \dfrac{{{U^2}}}{{2{R_2}}} = \dfrac{{{{120}^2}}}{{2.15}} = 480 \ne 160\)
=> điều giả sử ban đầu là sai
=> Cuộn dây không thuần cảm có điện trở $r$
- Ta có:
+ Ban đầu khi mắc vào hai đầu $A, M$ một ắc quy có suất điện động \(E{\rm{ }} = {\rm{ }}12V\), điện trở trong \({r_1} = 4\Omega \) thì \({I_1} = 0,1875\)
Theo định luật Ôm, ta có: \({I_1} = \dfrac{E}{{{R_b} + r}} = \dfrac{E}{{{R_1} + r + {r_1}}} \to {R_1} + {r_1} + r = \dfrac{E}{{{I_1}}} = 64 \to {R_1} + r = 60\Omega {\rm{}}({\rm{1}})\)
+ Khi mắc vào A,B một hiệu điện thế \(u = 120\sqrt 2 {\rm{cos100}}\pi {\rm{t}}\) ,\(R = {R_2}\) thì công suất tiêu thụ trên biến trở cực đại và bằng \(160W\)
Ta có: Công suất trên biến trở R đạt cực đại khi \({R_2}^2 = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}{\rm{ }}({\rm{2}})\)
Mặt khác, ta có: Công suất trên \({R_2}\):
\(\begin{array}{l}P{\rm{ = }}\dfrac{{{U^2}}}{{{{({R_2} + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R_2} = 160{\rm{W}}\\ \to \dfrac{{{R_2}}}{{{{({R_2} + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{160}}{{{{120}^2}}} = \dfrac{1}{{90}}90\\{R_2} = 2R_2^2 + 2{\rm{r}}R \to {R_2} + r = 45\end{array}\)
Kết hợp với (2) ta được: \(R_2^2 = {(45 - {R_2})^2} + {15^2} \to {R_2} = 25\Omega ,r = 20\Omega \)
Với \(r = 20\Omega \) thay vào (1) \( \to {R_1} = 60 - 20 = 40\Omega \)
\( \to \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{40}}{{25}} = 1,6\)
Điện năng được truyền từ nhà máy điện đến nơi tiêu thụ bằng đường dây tải điện một pha. Để giảm hao phí trên đường dây người ta tăng điện áp ở nơi truyền đi bằng máy tăng áp lí tưởng có tỉ số giữa số vòng dây của cuộn thứ cấp và số vòng dây của cuộn sơ cấp là k. Biết công suất của nhà máy điện không đổi, điện áp hiệu dụng giữa hai đầu cuộn sơ cấp không đổi, hệ số công suất của mạch điện bằng \(1\). Khi \(k = 10\) thì công suất hao phí trên đường dây bằng \(10\% \) công suất ở nơi tiêu thụ. Để công suất hao phí trên đường dây bằng \(5\% \) công suất ở nơi tiêu thụ thì k phải có giá trị là
-
A
\(19,1\).
-
B
\(13,8\).
-
C
\(15,0\).
-
D
\(5,0\).
Đáp án của giáo viên lời giải hay : B
Sử dụng biểu thức tính công suất hao phí: \(\Delta P = \dfrac{{{P^2}}}{{{{\left( {Ucos\varphi } \right)}^2}}}R\)
\(\Delta P = P - P'\)
Ta có
\(\begin{array}{l}\Delta P = 10\% P' \Rightarrow \Delta P = \dfrac{1}{{11}}P = \dfrac{{{P^2}}}{{{U^2}.co{{\rm{s}}^2}\varphi }}R{\rm{ }}\left( 1 \right)\\\Delta P = 5\% P' \Rightarrow \Delta P = \dfrac{1}{{21}}P = \dfrac{{{P^2}}}{{{k^2}{U^2}.co{{\rm{s}}^2}\varphi }}R{\rm{ }}\left( 2 \right)\end{array}\)
Chia 2 vế của 2 phương trình cho nhau, ta được
\(\dfrac{{{k^2}}}{{{{10}^2}}} = \dfrac{{21}}{{11}} \Rightarrow {k^2} = \dfrac{{2100}}{{11}} \Rightarrow k = 13,8\)
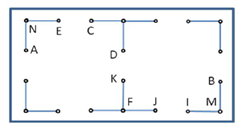
Trong giờ thực hành vật lí có sử dụng bộ thí nghiệm điện xoay chiều Vật lí 12 để tiến hành lắp mạch điện. Bảng lắp ráp mạch điện được vẽ lại như hình vẽ, với các chốt cắm có tên tương ứng. Một học sinh lắp mạch như sau: giữa E, C lắp cuộn cảm thuần có độ tự cảm \(31,85 mH\); giữa D, K lắp một điện trở \({\rm{R = 10 \Omega }}\); giữa J, I lắp một tụ xoay; giữa N, F lắp Vôn kế \(v_1\); giữa F, M lắp Vôn kế \(V_2\); giữa A, B duy trì một điện áp xoay chiều (\(12 V\) – \(50 Hz\)). Điều chỉnh góc xoay giữa hai bản tụ điện, quan sát đồng thời số chỉ của cả hai Vôn kế. Khi tổng số chỉ của hai Vôn kế đạt giá trị lớn nhất thì công suất của mạch lúc đó là
-
A
\(15,8 W\)
-
B
\(13,8 W\)
-
C
\(10,3 W\)
-
D
\(12,3 W\)
Đáp án của giáo viên lời giải hay : D
Số chỉ của vôn kế V1 là điện áp hiệu dụng của ULR, số chỉ của vôn kế V2 là điện áp hiệu dụng của UC.
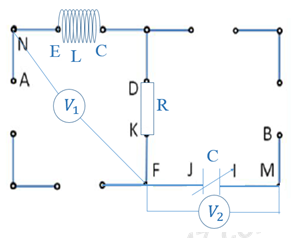
Ta có: Mạch điện gồm L, R, C mắc nối tiếp, tụ C thay đổi.
\(R = 10(\Omega );{Z_L} = 10(\Omega ) \Rightarrow {Z_L} = R\)
\({U_{LR}} = \dfrac{{{U_{AB}}}}{Z}.{Z_{RL}} = \dfrac{{{U_{AB}}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}.\sqrt {{R^2} + Z_L^2} \)
\({U_C} = \dfrac{{{U_{AB}}{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Tổng số chỉ của 2 vôn kế là:
\(U' = \dfrac{{{U_{AB}}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}.\sqrt {{R^2} + Z_L^2} + \dfrac{{{U_{AB}}{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{{U_{AB}}\left( {\sqrt {2{R^2}} + {Z_C}} \right)}}{{\sqrt {{R^2} + {{(R - {Z_C})}^2}} }} = \dfrac{{{U_{AB}}\left( {\dfrac{{\sqrt 2 R}}{{{Z_C}}} + 1} \right)}}{{\sqrt {\dfrac{{2{R^2}}}{{Z_C^2}} - 2\dfrac{R}{{{Z_C}}} + 1} }}\)
Đặt \(\dfrac{{\sqrt 2 R}}{{{Z_C}}} + 1 = a\)\( \Rightarrow U' = \dfrac{{{U_{AB}}.a}}{{\sqrt {{a^2} - (\sqrt 2 + 2)a + \sqrt 2 + 2} }} = \dfrac{{{U_{AB}}}}{{\sqrt {1 - \dfrac{{\sqrt 2 + 2}}{a} + \dfrac{{\sqrt 2 + 2}}{{{a^2}}}} }}\)
U’ max \( \Leftrightarrow \dfrac{1}{a} = \dfrac{{2 + \sqrt 2 }}{{2(2 + \sqrt 2 )}} = \dfrac{1}{2} \Rightarrow a = 2 \Rightarrow \dfrac{{\sqrt 2 R}}{{{Z_C}}} + 1 = 2 \Rightarrow {Z_C} = \sqrt 2 R = 10\sqrt 2 (\Omega )\)
Công suất của mạch lúc đó là:
\(P = \dfrac{{{U^2}}}{R}{\rm{co}}{{\rm{s}}^2}\varphi = \dfrac{{{{12}^2}}}{{10}}{\left( {\dfrac{{10}}{{\sqrt {{{10}^2} + {{(10 - 10\sqrt 2 )}^2}} }}} \right)^2} = 12,3({\rm{W}})\)
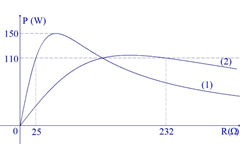
Lần lượt đặt vào hai đầu đoạn mạch xoay chiều RLC không phân nhánh (\(R\) là biến trở, \(L\) thuần cảm) hai điện áp xoay chiều \({u_1} = {U_{01}}\cos ({\omega _1}t + {\varphi _1})\) và \({u_2} = {U_{02}}\cos ({\omega _2}t + {\varphi _2})\) người ta thu được đồ thị công suất của mạch điện xoay chiều theo biến trở \(R\) như hình vẽ (đường 1 là của \(u_1\) và đường 2 là của \(u_2\)). Khi sử dụng điện áp \(u_2\) thì công suất tiêu thụ của mạch đạt giá trị lớn nhất là
-
A
\(113,4 W\)
-
B
\(116,9 W\)
-
C
\(112,3 W\)
-
D
\(114,5W\)
Đáp án của giáo viên lời giải hay : D
Sử dụng công thức: \({P_{\max }} = \dfrac{{{U^2}}}{{2{R_0}}}\) và \({R_1}{R_2} = R_0^2\)
Với R1, R2 có cùng giá trị công suất P
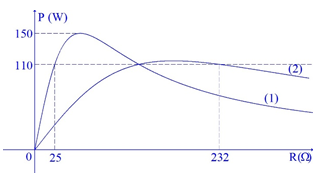
Ta có:
\({P_{1\max }} = \dfrac{{U_1^2}}{{2{R_{01}}}} = 150({\rm{W}})\); \(R_{01}^2 = {R_1}{R_2} = 25{R_2}\)
\({P_{2\max }} = \dfrac{{U_2^2}}{{2{R_{02}}}}\); \(R_{02}^2 = 232{R_2}\)
\({R_1} + {R_2} = \dfrac{{U_1^2}}{P} \Rightarrow 25 + {R_2} = \dfrac{{U_1^2}}{{110}} \Rightarrow U_1^2 = 110.\left( {25 + {R_2}} \right)\)
và \(R{'_1} + R{'_2} = \dfrac{{U_2^2}}{P} \Rightarrow {R_2} + 232 = \dfrac{{U_2^2}}{{110}} \Rightarrow U_2^2 = 110.({R_2} + 232)\)
(Lưu ý: \({R_2} = R{'_1}\))
\( \Rightarrow {P_{1\max }} = \dfrac{{U_1^2}}{{2{R_{01}}}} = \dfrac{{110.\left( {25 + {R_2}} \right)}}{{2\sqrt {25{R_2}} }} = 150 \Rightarrow {150^2}.100{R_2} = {110^2}{(25 + {R_2})^2} \Rightarrow {R_2} \approx 131(\Omega )\)
\({P_{2\max }} = \dfrac{{U_2^2}}{{2{R_{02}}}} = \dfrac{{110.({R_2} + 232)}}{{2\sqrt {232{R_2}} }} = 114,5({\rm{W}})\)
