Trong mạch \(RLC\) mắc nối tiếp, độ lệch pha giữa dòng điện và hiệu điện thế ở hai đầu đoạn mạch phụ thuộc:
-
A
Cường độ dòng điện hiệu dụng trong mạch
-
B
Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch
-
C
Cách chọn gốc tính thời gian
-
D
Tính chất của mạch điện
Đáp án của giáo viên lời giải hay : D
Sử dụng biểu thức tính độ lệch pha giữa điện áp và dòng điện trong mạch điện xoay chiều: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Độ lệch pha \(\varphi \) giữa \(u\) và \(v\) được tính bởi công thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Vì điện trở: \(R > 0 \to \tan \varphi \) phụ thuộc vào \({Z_L}\) và \({Z_C}\) => Phụ thuộc vào tính chất của mạch điện (mạch có tính dung kháng hay cảm kháng)
Trong mạch xoay chiều nối tiếp thì dòng điện nhanh hay chậm pha so với hiệu điện thế ở hai đầu của đoạn mạch là tuỳ thuộc:
-
A
R và C
-
B
L và C
-
C
L,C và ω
-
D
R,L,C và ω
Đáp án của giáo viên lời giải hay : C
+ Vận dụng biểu thức tính độ lệch pha giữa điện áp và dòng điện trong mạch điện xoay chiều: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Vận dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Vận dụng biểu thức tính dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)
+ Độ lệch pha \(\varphi \) giữa \(u\) và được tính bởi công thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Vì điện trở: \(R > 0 \to \tan \varphi \) phụ thuộc vào \({Z_L}\) và \({Z_C}\)
=> Phụ thuộc vào tính chất của mạch điện (mạch có tính dung kháng hay cảm kháng) hay chính là phụ thuộc vào \(L,C,\omega \)
Cho một mạch điện xoay chiều gồm \(RLC\) mắc nối tiếp. Hệ số công suất \(cos\varphi = {\rm{ }}0\) khi và chỉ khi:
-
A
\(\dfrac{1}{{\omega C}} = \omega L\)
-
B
\(P{\rm{ }} = {\rm{ }}{P_{max}}\)
-
C
\(R{\rm{ }} = {\rm{ }}0\)
-
D
\(U{\rm{ }} = {\rm{ }}{U_R}\)
Đáp án của giáo viên lời giải hay : C
Vận dụng biểu thức tính hệ số công suất: \({\rm{cos}}\varphi = \dfrac{R}{Z} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Ta có, hệ số công suất: \({\rm{cos}}\varphi = \dfrac{R}{Z} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
=> Để hệ số công suất \({\rm{cos}}\varphi = {\rm{0}}\) thì điện trở \(R = 0\)
Trong đoạn mạch RLC, mắc nối tiếp đang xảy ra hiện tượng cộng hưởng. Tăng dần tần số dòng điện và giữ nguyên các thông số của mạch, kết luận nào sau đây là không đúng?
-
A
Hệ số công suất của đoạn mạch giảm.
-
B
Cường độ hiệu của dòng điện giảm.
-
C
Hiệu điện thế hiệu dụng trên tụ điện tăng.
-
D
Hiệu điện thế hiệu dụng trên điện trở giảm.
Đáp án của giáo viên lời giải hay : C
+ Vận dụng các biểu thức khi mạch xảy ra cộng hưởng: \(\left\{ \begin{array}{l}{Z_L} = {Z_C}\\Z = R\\{I_{{\rm{max}}}},{P_{{\rm{max}}}},{Z_{\min }}\end{array} \right.\)
+ Vận dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Vận dụng biểu thức tính dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)
+ Vận dụng biểu thức định luật ôm: \(U = IZ\)
+ Mạch cộng hưởng thì khi đó: \(\left\{ \begin{array}{l}{Z_L} = {Z_C}\\Z = R\end{array} \right.\)
+ Ta có: \(\left\{ \begin{array}{l}{Z_L} = \omega L = 2\pi fL\\{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\end{array} \right.\)
+ Khi tăng dần tần số dòng điện và giữ nguyên các thông số của mạch thì \({Z_L}\) tăng và\({Z_C}\) giảm
=> \(Z\) tăng
=> hệ số công suất: \({\rm{cos}}\varphi = \frac{R}{Z}\) giảm và \(I\) giảm
=> A,B,D đúng
+ Vì \({Z_C}\) và \(I\) giảm => \({U_C} = I.{Z_C}\) cũng giảm => C sai
Một mạch điện gồm \(R = 60\Omega \), cuộn cảm thuần có độ tự cảm \(L = \frac{{0,4}}{\pi }H\) và tụ điện có điện dung \(C = \frac{{{{10}^{ - 4}}}}{\pi }F\) mắc nối tiếp, biết \(f = 50Hz\).Tính tổng trở trong mạch, và độ lệch pha giữa \(u\) và \(i\)?
\(cos\varphi\)
-
A
\(60\Omega ;\dfrac{\pi }{4}rad\)
-
B
\(60\sqrt 2 \Omega ;\dfrac{\pi }{4}rad\)
-
C
\(60\sqrt 2 \Omega ; - \dfrac{\pi }{4}rad\)
-
D
\(60\Omega ; - \dfrac{\pi }{4}rad\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)
+ Sử dụng biểu thức tính tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính độ lệch pha giữa điện áp và dòng điện trong mạch điện xoay chiều: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Ta có:
+ Cảm kháng: \({Z_L} = \omega L = 2\pi f.L = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega \)
+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi f.C}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{60}^2} + {{\left( {40 - 100} \right)}^2}} = 60\sqrt 2 \Omega \)
+ Độ lệch pha của điện áp so với dòng điện trong mạch:
\(\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{40 - 100}}{{60}} = - 1\\ \to \varphi = - \dfrac{\pi }{4}\end{array}\)
Mạch điện gồm cuộn dây có điện trở \(R = 30\Omega \) , cuộn cảm thuần có hệ số tự cảm \(L = \frac{{0,6}}{\pi }H\) mắc nối tiếp vào tụ điện có điện dung \(C = \frac{{100}}{\pi }\mu F\). Điện áp giữa hai đầu đoạn mach biến thiên điều hòa với tần số \(50Hz\). Tổng trở của đoạn mach có giá trị là:
-
A
\(50\Omega \)
-
B
\(40\Omega \)
-
C
\(60\Omega \)
-
D
\(45\Omega \)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)
+ Sử dụng biểu thức tính tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Cảm kháng: \({Z_L} = \omega L = 2\pi f.L = 2\pi .50.\frac{{0,6}}{\pi } = 60\Omega \)
+ Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}} = \frac{1}{{2\pi .50.\frac{{100}}{\pi }{{.10}^{ - 6}}}} = 100\Omega \)
+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{30}^2} + {{\left( {60 - 100} \right)}^2}} = 50\Omega \)
Cho đoạn mạch \(RC\) mắc nối tiếp vào nguồn điện xoay chiều. Biết \(R = 30\Omega \), và các điện áp như sau: \({U_R} = 90V\), \({U_C} = 150V\), tần số dòng điện là \(50Hz\). Hãy tìm điện dung của tụ:
-
A
\(50F\)
-
B
\(50.10{^{ - 3}}F\)
-
C
\(\dfrac{{{{10}^{ - 3}}}}{{5\pi }}F\)
-
D
Không đáp án
Đáp án của giáo viên lời giải hay : C
+ Vận dụng biểu thức định luật ôm: \(I = \dfrac{U}{Z}\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
Ta có:
+ Cường độ dòng điện trong mạch: \(I = \dfrac{{{U_R}}}{R} = \dfrac{{90}}{{30}} = 3A\)
+ Dung kháng: \({Z_C} = \dfrac{{{U_C}}}{I} = \dfrac{{150}}{3} = 50\Omega \)
Mặt khác, ta có: \({Z_C} = \dfrac{1}{{\omega C}} \to C = \dfrac{1}{{\omega {Z_C}}} = \dfrac{1}{{2\pi f.{Z_C}}} = \dfrac{1}{{2\pi .50.50}} = \dfrac{{{{10}^{ - 3}}}}{{5\pi }}F\)
Một cuộn dây có điện trở thuần \(40\Omega \). Độ lệch pha giữa điện áp hai đầu cuộn dây và dòng điện qua cuộn dây là \({45^0}\). Tính cảm kháng và và tổng trở của cuộn dây?
-
A
\({Z_L} = 50\Omega ;Z = 50\sqrt 2 \Omega \)
-
B
\({Z_L} = 49\Omega ;Z = 50\Omega \)
-
C
\({Z_L} = 40\Omega ;Z = 40\sqrt 2 \Omega \)
-
D
\({Z_L} = 30\Omega ;Z = 30\sqrt 2 \Omega \)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính độ lệch pha giữa điện áp và dòng điện trong mạch điện xoay chiều: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Sử dụng biểu thức tính tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Mạch của ta gồm có cảm kháng \({Z_L}\) và điện trở thuần \(R = 40\Omega \)
+ Độ lệch pha giữa điện áp hai đầu cuộn dây và dòng điện qua cuộn dây là:
\(\begin{array}{l}\tan \varphi = \dfrac{{{Z_L}}}{R} \leftrightarrow \tan {45^0} = \dfrac{{{Z_L}}}{R}\\ \to {Z_L} = R\tan {45^0} = 40\Omega \end{array}\)
+ Tổng trở của cuộn dây: \({Z_{cd}} = \sqrt {{R^2} + Z_L^2} = \sqrt {{{40}^2} + {{40}^2}} = 40\sqrt 2 \Omega \)
Mạch \(RLC\) mắc nối tiếp có \(C = \dfrac{{{{10}^{ - 4}}}}{\pi }F\); \(L = \dfrac{1}{\pi }H\). Mạch điện trên được mắc vào dòng điện trong mạch xoay chiều có \(f\) thay đổi. Tìm \(f\) để dòng điện trong mạch đạt giá trị cực đại?
-
A
\(100{\rm{ }}Hz\)
-
B
\(60{\rm{ }}Hz\)
-
C
\(50Hz\)
-
D
\(120{\rm{ }}Hz\)
Đáp án của giáo viên lời giải hay : C
Vận dụng bài toán \(f\) thay đổi để \({I_{{\rm{max}}}}\) khi đó mạch xảy ra cộng hưởng: \({Z_L} = {Z_C}\)
Khi \(f\) thay đổi để dòng điện trong mạch đạt giá trị cực đại \({I_{{\rm{max}}}}\) thì khi đó mạch xay ra cộng hưởng: \({Z_L} = {Z_C}\)
\({Z_L} = {Z_C} \leftrightarrow 2\pi f.L = \dfrac{1}{{2\pi f.C}} \to f = \dfrac{1}{{2\pi \sqrt {LC} }} = \dfrac{1}{{2\pi \sqrt {\dfrac{1}{\pi }.\dfrac{{{{10}^{ - 4}}}}{\pi }} }} = 50Hz\)
Mạch \(RLC\) mắc nối tiếp khi đặt vào hai đầu mạch hiệu điện thế xoay chiều \(U{\rm{ }} = {\rm{ }}50{\rm{ }}V\) thì cường độ dòng điện trong mạch là \(2A\). Biết độ lệch pha giữa \(u\) và \(i\) là \(\dfrac{\pi }{6}\), giá trị điện trở trong mạch điện là:
-
A
\(12,5\Omega \)
-
B
\(12,5\sqrt 2 \Omega \)
-
C
\(12,5\sqrt 3 \Omega \)
-
D
\(125\sqrt 3 \Omega \)
Đáp án của giáo viên lời giải hay : C
+ Vận dụng biểu thức định luật ôm: \(I = \dfrac{U}{Z}\)
+ Vận dụng biểu thức: \({\rm{cos}}\varphi = \dfrac{R}{Z}\)
+ Ta có, tổng trở của mạch \(Z = \dfrac{U}{I} = \dfrac{{50}}{2} = 25\Omega \)
+ Độ lệch pha giữa \(u\) và \(i\) là \(\varphi = \dfrac{\pi }{6}\)
=> \({\rm{cos}}\varphi = \dfrac{R}{Z} \to R = Z.c{\rm{os}}\varphi = 25.c{\rm{os}}\dfrac{\pi }{6} = 12,5\sqrt 3 \Omega \)
Mạch \(RLC\) mắc nối tiếp có \(L\) thay đổi được mắc vào mạch điện \(200V{\rm{ }} - {\rm{ }}50{\rm{ }}Hz\). Khi hiện tượng cộng hưởng xảy ra công suất trong mạch là \(100W\). Tìm điện trở trong mạch?
-
A
\(300\Omega \)
-
B
\(400\Omega \)
-
C
\(500\Omega \)
-
D
\(600\Omega \)
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức tính công suất khi xảy ra cộng hưởng: \({P_{{\rm{max}}}} = \frac{{{U^2}}}{R}\)
Ta có, khi xảy ra cộng hưởng thì công suất của mạch đạt cực đại: \({P_{{\rm{max}}}} = \frac{{{U^2}}}{R}\)
\( \to R = \frac{{{U^2}}}{{{P_{{\rm{max}}}}}} = \frac{{{{200}^2}}}{{100}} = 400\Omega \)
Điện trở \(R = 30\Omega \) và một cuộn dây mắc nối tiếp với nhau. Khi đặt hiệu điện thế không đổi \(24V\) vào hai đầu mạch này thì dòng điện qua nó là \(0,6A\). Khi đặt một hiệu điện thế xoay chiều có \(f{\rm{ }} = {\rm{ }}50Hz\) vào hai đầu mạch thì dòng điện trong mạch lệch pha \({45^0}\) so với hiệu điện thế này. Tính điện trở thuần \(r\) và \(L\) của cuộn dây?
-
A
\(r = 11\Omega ;L = 0,17H\)
-
B
\(r = 13\Omega ;L = 0,27H\)
-
C
\(r = 10\Omega ;L = 0,127H\)
-
D
\(r = 10\Omega ;L = 0,87H\)
Đáp án của giáo viên lời giải hay : C
+ Xác định tổng trở của mạch khi đặt hiệu điện thế không đổi
+ Vận dụng biểu thức định luật Ôm: \(I = \frac{U}{Z}\)
+ Vận dụng biểu thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Vận dụng biểu thức tính cảm kháng: \({Z_L} = \omega L = 2\pi fL\)
+ Khi đặt hiệu điện thế không đổi thì tổng trở của mạch: \(Z = R + r\)
+ Ta có: \(Z = \frac{U}{I} = \frac{{24}}{{0,6}} = 40\Omega \)
Ta suy ra: \(R + r = 40 \to r = 40 - R = 40 - 30 = 10\Omega \)
+ Khi đặt hiệu điện thế xoay chiều có \(f = 50Hz\) vào hai đầu mạch thì \(u\) và \(i\) lệch pha nhau góc \(\varphi = {45^0}\)
Ta có: \(\tan \varphi = \frac{{{Z_L}}}{{R + r}} \leftrightarrow \tan {45^0} = \frac{{{Z_L}}}{{40}} \to {Z_L} = 40\tan {45^0} = 40\Omega \)
+ Mặt khác, ta có: \({Z_L} = \omega L = 2\pi f.L \to L = \frac{{{Z_L}}}{{2\pi f}} = \frac{{40}}{{2\pi .50}} = 0,127H\)
Mạch gồm \(2\) trong \(3\) phần tử \(R,L,C\) nối tiếp. Hiệu điện thế ở hai đầu mạch và dòng điện trong mạch là \(u = 50\sqrt 2 \sin \left( {100\pi t} \right)V\) và \(i = 2\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)A\). Hai phần tử đó là những phần tử:
-
A
\(R,C\)
-
B
\(R,L\)
-
C
\(L,C\)
-
D
Cả 3 câu đều sai
Đáp án của giáo viên lời giải hay : D
+ Sử dụng các biến đổi lượng giác
+ Vận dụng độ lệch pha giữa \(u\) và \(i\) từ đó xác định các phần từ trong mạch
+ Ta có: \(u = 50\sqrt 2 \sin \left( {100\pi t} \right)V = 50\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)V\)
\(i = 2\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)A\)
Ta suy ra: Độ lệch pha giữa \(u\) và \(i\) là \(\varphi = 0\) hay \(u\) và \(i\) cùng pha với nhau
=> Mạch chỉ chứa R hoặc mạch RLC trong đó \({Z_L} = {Z_C}\)
=> Cả 3 phương án A, B, C đều sai
Trong một đọan mạch \(R,L,C\) mắc nối tiếp, lần lượt gọi \({U_{0R}},{U_{0L}},{\rm{ }}{U_{0C}}\) là hiệu điện thế cực đại giữa hai đầu điện trở, cuộn dây, tụ điện. Biết \(2{U_{0R}} = {\rm{ }}{U_{0L}} = {\rm{ }}2{U_{0C}}\) . Xác định độ lệch pha giữa cường độ dòng điện và hiệu điện thế ?
-
A
\(u\) sớm pha hơn \(i\) góc \(\frac{\pi }{4}\)
-
B
\(u\) trễ pha hơn \(i\) góc \(\frac{\pi }{4}\)
-
C
\(u\) sớm pha hơn \(i\) góc \(\frac{\pi }{3}\)
-
D
\(u\) sớm pha hơn \(i\) góc \(\frac{\pi }{3}\)
Đáp án của giáo viên lời giải hay : A
Vận dụng biểu thức tính độ lệch pha giữa \(u\) và \(i\) : \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{{U_L} - {U_C}}}{{{U_R}}}\)
Ta có độ lệch pha giữa \(u\) và \(i\) được xác định bởi biểu thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{{U_L} - {U_C}}}{{{U_R}}} = \frac{{{U_{0L}} - {U_{0C}}}}{{{U_{0R}}}}\) (1)
Mặt khác, theo đầu bài ta có:
\(2{U_{0R}} = {U_{0L}} = 2{U_{0C}} \to \left\{ \begin{array}{l}{U_{0R}} = {U_{0C}}\\{U_{0L}} = 2{U_{0C}}\end{array} \right.\)
Thay vào (1) ta được: \(\tan \varphi = \frac{{2{U_{0C}} - {U_{0C}}}}{{{U_{0C}}}} = 1 \to \varphi = \frac{\pi }{4}\)
=> \(u\) sớm pha hơn \(i\) một góc \(\frac{\pi }{4}\)
Một đoạn mạch xoay chiều gồm một điện trở thuần \(R = 100\Omega \), cuộn cảm thuần có độ tự cảm \(L = \dfrac{1}{\pi }H\) và một tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 4}}}}{{2\pi }}F\) mắc nối tiếp giữa hai điểm có hiệu điện thế \(u = 200\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)V\) . Công suất của mạch khi đó có giá trị là:
-
A
\(200W\)
-
B
\(100\sqrt 2 {\rm{W}}\)
-
C
\(200\sqrt 2 {\rm{W}}\)
-
D
\(100W\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Sử dụng biểu thức tính tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính công suất: \(P = UI\cos \varphi = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \)
+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{{2\pi }}}} = 200\Omega \)
+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{100}^2} + {{\left( {100 - 200} \right)}^2}} = 100\sqrt 2 \Omega \)
+ Công suất của mạch: \(P = UI\cos \varphi = \dfrac{{{U^2}}}{{{Z^2}}}R = \dfrac{{{{200}^2}}}{{{{\left( {100\sqrt 2 } \right)}^2}}}.100 = 200W\)
Đặt vào cuộn dây có điện thở thuần \(r\) và độ tự cảm \(L\) một hiệu điện thế \(u = {U_0}cos100\pi t{\rm{ }}\left( V \right)\). Dòng điện qua cuộn dây là \(10A\) và trễ pha \(\dfrac{\pi }{3}\) so với \(u\). Biết công suất tiêu hao trên cuộn dây là \(P{\rm{ }} = {\rm{ }}200W\). Giá trị của \({U_0}\) bằng:
-
A
\(20\sqrt 2 V\)
-
B
\(40{\rm{ }}V\)
-
C
\(40\sqrt 2 V\)
-
D
\(80{\rm{ }}V\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính công suất: \(P = UIc{\rm{os}}\varphi \)
+ Sử dụng biểu thức liên hệ giữa giá trị cực đại – giá trị hiệu dụng: \({U_0} = U\sqrt 2 \)
Theo đầu bài ta có độ lệch pha của \(u\) so với \(i\) là \(\varphi = \dfrac{\pi }{3}\)
+ Công suất tiêu hao: \(P = UI\cos \varphi \to U = \dfrac{P}{{I\cos \varphi }} = \dfrac{{200}}{{10.c{\rm{os}}\dfrac{\pi }{3}}} = 40V\)
+ Ta suy ra: \({U_0} = U\sqrt 2 = 40\sqrt 2 V\)
Mạch \(RLC\) nối tiếp. Cho \(U = {\rm{ }}200V\); \(R = 40\sqrt 3 \Omega \); \(L = \dfrac{{0,5}}{\pi }(H)\); \(C = \dfrac{{{{10}^{ - 3}}}}{{9\pi }}(F)\); \(f = 50Hz\). Cường độ hiệu dụng trong mạch là:
-
A
\(2A\)
-
B
\(2,5A\)
-
C
\(4A\)
-
D
\(5A\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Sử dụng biểu thức tính tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức định luật Ôm: \(I = \dfrac{U}{Z}\)
+ Cảm kháng: \({Z_L} = \omega L = 2\pi f.L = 2\pi .50.\dfrac{{0,5}}{\pi } = 50\Omega \)
+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi f.C}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{{9\pi }}}} = 90\Omega \)
+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{\left( {40\sqrt 3 } \right)}^2} + {{\left( {50 - 90} \right)}^2}} = 80\Omega \)
+ Cường độ dòng điện hiệu dụng trong mạch: \(I = \dfrac{U}{Z} = \dfrac{{200}}{{80}} = 2,5A\)
Mạch gồm điện trở, cuộn thuần cảm và tụ điện nối tiếp. Biết hiệu điện thế hiệu dụng là \({U_R} = 120V\), \({U_C} = {\rm{ }}100V\),\({U_L} = {\rm{ }}50V\). Nếu mắc thêm một tụ điện có điện dung bằng giá trị và song song với tụ điện nói trên thì hiệu điện thế trên điện trở là bao nhiêu? Coi hiệu điện thế hai đầu mạch là không đổi.
-
A
\(120V\)
-
B
\(130V\)
-
C
\(140V\)
-
D
\(150V\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính hiệu điện thế của toàn mạch: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \)
+ Xét tỉ lệ giữa \({Z_L},{Z_C},R\)
+ Vận dụng biểu thức tính điện dung của tụ khi mắc song song: \({C_b} = {C_1} + {C_2} + ... + {C_n}\)
+ Vận dụng biểu thức tính tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Hiệu điện thế hai đầu mạch: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{120}^2} + {{\left( {100 - 50} \right)}^2}} = 130V\)
+ Theo đầu bài, ta có: \(\left\{ \begin{array}{l}{U_R} = 120V\\{U_C} = 100V\\{U_L} = 50V\end{array} \right. \to \left\{ \begin{array}{l}{Z_L} = \dfrac{R}{{2,4}}\\{Z_C} = \dfrac{R}{{1,2}}\end{array} \right.\)
+ Khi mắc thêm một tụ điện có điện dung bằng giá trị và song song với tụ điện cũ thì khi đó:
\(C' = {C_1} + {C_2} = 2C \to {Z_{C'}} = \dfrac{1}{{\omega C'}} = \dfrac{{{Z_C}}}{2} = \dfrac{R}{{2.1,2}} = \dfrac{R}{{2,4}}\)
+ Tổng trở của mạch khi đó: \(Z' = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_{C'}}} \right)}^2}} = R\)
Nhân cả hai vế với \(I'\) ta được: \(U = {U_R}' = 130V\)
Dòng điện chạy qua đoạn mạch xoay chiều có dạng \(i = 2cos100\pi t\left( A \right)\), hiệu điện thế giữa hai đầu đoạn mạch có giá trị hiệu dụng là \(12V\) và sớm pha \(\dfrac{\pi }{3}\) so với dòng điện. Biểu thức của hiệu điện thế giữa hai đầu đoạn mạch là:
-
A
\(u = 12\cos \left( {100\pi t} \right)V\)
-
B
\(u = 12\sqrt 2 {\rm{cos}}\left( {{\rm{100}}\pi {\rm{t}}} \right)V\)
-
C
\(u = 12\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{3}} \right)\)
-
D
\(u = 12\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{3}} \right)V\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng mối liên hệ giữa điện áp hiệu dụng và điện áp cực đại: \({U_0} = U\sqrt 2 \)
+ Xác định độ lệch pha giữa \(u\) và \(i\)
+ Từ phương trình \(i\) => viết phương trình \(u\)
Ta có:
+ Hiệu điện thế hiệu dụng \(U = 12V \to {U_0} = U\sqrt 2 = 12\sqrt 2 V\)
+ \(u\) sớm pha hơn \(i\) một góc \(\dfrac{\pi }{3}\) , ta suy ra: \({\varphi _u} - {\varphi _i} = \dfrac{\pi }{3} \to {\varphi _u} = \dfrac{\pi }{3} + 0 = \dfrac{\pi }{3}rad\)
=> Biểu thức của hiệu điện thế giữa hai đoạn mạch là: \(u = 12\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{3}} \right)V\)
Điện trở \(R = 80\Omega \) nối tiếp với cuộn thuần cảm \(L = \dfrac{{0,8}}{\pi }\left( H \right)\) vào hiệu điện thế \(u = 120\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{4}} \right)V\). Biểu thức dòng điện trong mạch là:
-
A
\(i = 1,5\cos \left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
B
\(i = 1,5\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
C
\(i = 1,5\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)A\)
-
D
\(i = 1,5cos\left( {100\pi t} \right)A\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức định luật Ôm: \({I_0} = \dfrac{{{U_0}}}{Z}\)
+ Sử dụng biểu thức tính độ lệch pha giữa \(u\) và \(i\): \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{{0,8}}{\pi } = 80\Omega \)
+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + Z_L^2} = \sqrt {{{80}^2} + {{80}^2}} = 80\sqrt 2 \Omega \)
+ Cường độ dòng điện cực đại trong mạch: \({I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{120\sqrt 2 }}{{80\sqrt 2 }} = 1,5A\)
+ Độ lệch pha giữa điện áp và dòng điện: \(\tan \varphi = \dfrac{{{Z_L}}}{R} = \dfrac{{80}}{{80}} = 1 \to \varphi = \dfrac{\pi }{4}\)
=> Điện áp nhanh pha hơn dòng điện một góc \(\dfrac{\pi }{4}\)
Ta suy ra: \({\varphi _u} - {\varphi _i} = \dfrac{\pi }{4} \to {\varphi _i} = {\varphi _u} - \dfrac{\pi }{4} = \dfrac{\pi }{4} - \dfrac{\pi }{4} = 0\)
=> Biểu thức dòng điện trong mạch khi đó: \(i = 1,5\cos \left( {100\pi t} \right)A\)
Một mạch điện xoay chiều gồm các linh kiện lý tưởng \(R,L,C\) mắc nối tiếp. Tần số góc riêng của mạch là \({\omega _0}\), điện trở \(R\) có thể thay đổi. Hỏi cần phải đặt vào mạch một điện áp xoay chiều có giá trị hiệu dụng không đổi, có tần số góc \(\omega \) bằng bao nhiêu để điện áp hiệu dụng \({U_{RL}}\) không phụ thuộc vào \(R\)?
-
A
\(\omega = \dfrac{{{\omega _0}}}{{\sqrt 2 }}\)
-
B
\(\omega = {\omega _0}\)
-
C
\(\omega = {\omega _0}\sqrt 2 \)
-
D
\(\omega = 2{\omega _0}\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}\)
+ Viết biểu thức tính điện áp hiệu dụng \({U_{RL}} = I{Z_{RL}}\)
Ta có
\(\left\{ \begin{array}{l}\omega = \dfrac{1}{{\sqrt {LC} }}\\{U_{RL}} = I.{Z_{RL}} = \dfrac{{U.{Z_{RL}}}}{Z} = \dfrac{{U.\sqrt {\left( {{R^2} + Z_L^2} \right)} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}\end{array} \right.\)
Từ biểu thức trên ta có để \({U_{RL}}\) không phụ thuộc vào \(R\) ta suy ra:
\({Z_C} = 2{Z_L} = > \dfrac{1}{{\omega C}} = 2\omega L = > \omega = \dfrac{1}{{\sqrt 2 .\sqrt {LC} }} = \dfrac{{{\omega _0}}}{{\sqrt 2 }}\)
Đoạn mạch xoay chiều \(RLC\) nối tiếp có tụ \(C\) thay đổi được. \({U_R} = 60V,{U_L} = 120V\),\({U_{C}} = 60V\). Thay đổi tụ \(C\) để điện áp hiệu dụng hai đầu \(C\) là \(U{'_C} = 40V\) thì điện áp hiệu dụng hai đầu điện trở \(R\) bằng:
-
A
\(13,3V\)
-
B
\(53,1V\)
-
C
\(80V\)
-
D
\(90V\)
Đáp án của giáo viên lời giải hay : B
Sử dụng biểu thức tính hiệu điện thế của toàn mạch: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \)
+ Lúc đầu ta có \({U_L} = {\rm{ }}2{U_R}\) và điện áp toàn mạch \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = 60\sqrt 2 V\)
+ Lúc sau khi thay đổi tụ \(C\) ta vẫn có \(U{'_L} = 2U{'_R}\) ( do \({Z_L}\) và \(R\) không đổi ).
Ngoài ra \(U' = U\) nên:
\(\begin{array}{l}U' = \sqrt {{U'_R}^2 + \left( {U{'_L} - U{'_C}}\right) ^2} = \sqrt {{U'_R}^2 + \left( {2U{'_R} - U{'_C}} \right)^2} = 60\sqrt 2 V\\ \to 60\sqrt 2 = \sqrt {{U'_R}^2 + \left( {2U{'_R} - 40} \right)^2} \\ \to U{'_R} = 53,1V\end{array}\)
Một đoạn mạch gồm cuộn dây có điện trở thuần \(r = 10\Omega \) và độ tự cảm \(L = \frac{{0,1}}{\pi }H\) mắc nối tiếp với điện trở thuần \(R = 20\Omega \) và tụ điện \(C = \frac{{{{10}^{ - 3}}}}{{4\pi }}F\). Đặt vào hai đầu đoạn mạch một hiệu điện thế \(u = 180\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)V\). Độ lệch pha của hiệu điện thế giữa hai đầu cuộn dây và hai đầu tụ điện là:
-
A
\( - \frac{\pi }{4}\)
-
B
\( - \frac{{3\pi }}{4}\)
-
C
\(\frac{{3\pi }}{4}\)
-
D
\(\frac{\pi }{4}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Ta có: \(\tan \varphi = \frac{{{Z_L}}}{r} = 1 = > {\varphi _d} = \frac{\pi }{4}\)
Mặt khác ta lại có \({\varphi _C} = - \frac{\pi }{2}\)
=> Độ lệch pha của hiệu điện thế giữa hai đầu cuộn dây và hai đầu tụ điện là \(\frac{\pi }{4} - \left( { - \frac{\pi }{2}} \right) = \frac{{3\pi }}{4}\)
Đặt điện áp xoay chiều có giá trị hiệu dụng \(60V\) vào hai đầu đoạn mạch \(R,{\rm{ }}L,{\rm{ }}C\) mắc nối tiếp thì cường độ dòng điện qua đoạn mạch là \({i_1} = {I_0}{\rm{cos}}\left( {100\pi t + \dfrac{\pi }{4}} \right)A\). Nếu ngắt bỏ tụ điện C thì cường độ dòng điện qua đoạn mạch là \({i_2} = {I_0}{\rm{cos}}\left( {100\pi t - \dfrac{\pi }{{12}}} \right)A\). Điện áp hai đầu đoạn mạch là:
-
A
\(u = 60\sqrt 2 \cos (100\pi t - \dfrac{\pi }{{12}})V\)
-
B
\(u = 60\sqrt 2 \cos (100\pi t - \dfrac{\pi }{6})V\)
-
C
\(u = 60\sqrt 2 \cos (100\pi t + \dfrac{\pi }{{12}})V\)
-
D
\(u = 60\sqrt 2 \cos (100\pi t + \dfrac{\pi }{6})V\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng mối liên hệ giữa giá trị hiệu dụng và giá trị cực đại: \(\left\{ \begin{array}{l}I = \dfrac{{{I_0}}}{{\sqrt 2 }}\\U = \dfrac{{{U_0}}}{{\sqrt 2 }}\end{array} \right.\)
+ Sử dụng biểu thức định luật Ôm: \(I = \dfrac{U}{Z}\)
+ Vận dụng biểu thức: \({\rm{cos}}\varphi = \dfrac{R}{Z}\)
+ Ta có: \({I_1} = {I_2} = \dfrac{{{I_0}}}{{\sqrt 2 }} \to {Z_1} = {Z_2}\)
+ Vì \(R\) không đổi \( \to \dfrac{R}{{{Z_1}}} = \dfrac{R}{{{Z_2}}} \leftrightarrow c{\rm{os}}{\varphi _1} = c{\rm{os}}{\varphi _2}\)
$ \to \left[ \begin{gathered}
{\varphi _1} = {\varphi _2}(loai) \hfill \\
{\varphi _1} = - {\varphi _2} \hfill \\
\end{gathered} \right.$
Với \(\varphi \) - độ lệch pha của \(u\) và \(i\)
Ta suy ra: \(\varphi = {\varphi _u} - {\varphi _{{i_1}}} = {\varphi _{{i_2}}} - {\varphi _u}\) (do \({\varphi _1} = - {\varphi _2}\) )
\( \to {\varphi _u} = \dfrac{{{\varphi _{{i_1}}} + {\varphi _{{i_2}}}}}{2} = \dfrac{{\dfrac{\pi }{4} - \dfrac{\pi }{{12}}}}{2} = \dfrac{\pi }{{12}}rad\)
+ Điện áp cực đại \({U_0} = U\sqrt 2 = 60\sqrt 2 V\)
=> Biểu thức điện áp \(u = 60\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{{12}}} \right)V\)
Đoạn mạch \(RLC\) có \(L\) thay đổi được mắc vào mạng điện xoay chiều có hiệu điện thế không đổi. Viết công thức xác định \({Z_L}\) để hiệu điện thế hai đầu tụ điện đạt cực đại?
-
A
\({Z_L} = 2{Z_C}\)
-
B
\({Z_L} = R\)
-
C
\({Z_L} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)
-
D
\({Z_L} = {Z_C}\)
Đáp án của giáo viên lời giải hay : D
Bài toán L thay đổi để \({U_{{C_{{\rm{max}}}}}}\)khi đó mạch xảy ra công hưởng
Ta có hiệu điện thế \(2\) đầu tụ \({U_C} = I.{Z_C} = \frac{{U.{Z_C}}}{Z} = \frac{{U.{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Thay đổi \(L\) để \({U_C}\) đạt cực đại thì \({Z_L} = {\rm{ }}{Z_C}\)
Đoạn mạch \(RLC\) có \(R\) thay đổi được mắc vào mạng điện xoay chiều có hiệu điện thế không đổi. Xác định \(R\) để hiệu điện thế hai đầu cuộn cảm đạt cực đại?
-
A
\(R\) tiến về \(\infty \)
-
B
\(R\) tiến về \(0\)
-
C
\(R = \left| {{Z_L} - {Z_C}} \right|\)
-
D
\(R = {Z_L} - {Z_C}\)
Đáp án của giáo viên lời giải hay : B
Viết biểu thức tính hiệu điện thế giữa hai đầu cuộn cảm: \({U_L} = I{Z_L}\)
Ta có: \({U_L} = I.{Z_L} = \frac{U}{Z}{Z_L} = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{Z_L}\)
Vì \(R\) thay đổi nên để hiệu điện thế hai đầu cuộn cảm đạt cực đại thì \(R\) tiến về \(0\)
Mạch \(RLC\) có \(R = 20\Omega ,L = \dfrac{{0,4}}{\pi }H\) và tụ điện \(C\) có thể thay đổi. Mắc mạch điện trên vào mạng điện \(220V - 50Hz\). Tìm giá trị của \(C\) để \({U_R}\) đạt giá trị cực đại?
-
A
\(C = \dfrac{{{{10}^{ - 4}}}}{{4\pi }}F\)
-
B
\(C = \dfrac{{{{4.10}^{ - 4}}}}{\pi }F\)
-
C
\(C = \dfrac{{{{2,5.10}^{ - 4}}}}{\pi }F\)
-
D
\(C = \dfrac{{{{10}^{ - 3}}}}{{6\pi }}F\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L = 2\pi fL\)
+ Bài toán C biến thiên để \({U_{{R_{{\rm{max}}}}}}\)
+ Vận dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Ta có: \(\left\{ \begin{array}{l}R = 20\Omega \\{Z_L} = \omega L = 2\pi f.L = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega \end{array} \right.\)
+ C biên thiên để \({U_{{R_{{\rm{max}}}}}}\) => mạch cộng hưởng \({Z_L} = {Z_C} = 40\Omega \)
+ Lại có \({Z_C} = \dfrac{1}{{\omega C}} \to C = \dfrac{1}{{\omega {Z_C}}} = \dfrac{1}{{2\pi f.{Z_C}}} = \dfrac{1}{{2\pi .50.40}} = \dfrac{{{{2,5.10}^{ - 4}}}}{\pi }F\)
Mạch \(RLC\) mắc theo thứ tự có\(L\) thay đổi, \(R = 50{\rm{ }}\Omega ,C = \frac{{{{10}^{ - 4}}}}{\pi }F\). Mắc mạch điện trên vào mạng điện xoay chiều \(220{\rm{ }}V{\rm{ }} - {\rm{ }}50{\rm{ }}Hz\). \(L\) thay đổi để \({U_{R{L_{{\rm{max}}}}}}\), giá trị của \(L\) khi đó là:
-
A
\(\frac{1}{\pi }\)
-
B
\(\frac{2}{\pi }H\)
-
C
\(\frac{1,2}{{\pi }}H\)
-
D
\(\frac{{0,25}}{\pi }H\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)
+ Biến đổi đại số, xét hàm của biểu thức \({U_{RL}}\)
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Ta có: \(\left\{ \begin{array}{l}R = 50\Omega \\{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi f.C}} = \frac{1}{{2\pi .50.\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \end{array} \right.\)
Ta có: \({U_{RL}} = I{Z_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \frac{U}{{\sqrt {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} }}\)
URLmax \( \leftrightarrow {\left( {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} \right)_{\min }}\)
\(y = 1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}\\y' = (1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}})' = \frac{{2{Z_L}^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_L^2)}^2}}}\\y' = 0 \leftrightarrow 2{Z_L}^2 - 2{R^2} - 2{Z_L}{Z_C} = 0\)
Khi đó:
Khảo sát sự biến thiên của y ta được:
\({y_{\max }} = \frac{{2RU}}{{\sqrt {4{{\rm{R}}^2} + Z_C^2} - {Z_C}}}\) khi \({Z_L} = \frac{{{Z_C} + \sqrt {4{{\rm{R}}^2} + Z_C^2} }}{2}\)
\( \Rightarrow {Z_L} = \frac{{100 + \sqrt {{{4.50}^2} + {{100}^2}} }}{2} = 50.\left( {1 + \sqrt 2 } \right)\Omega \)
Mà \({Z_L} = \omega L = 2\pi fL\)
Suy ra \(L = \frac{{{Z_L}}}{{2\pi f}} = \frac{{50\left( {1 + \sqrt 2 } \right)}}{{2\pi .50}} = \frac{{1,2}}{\pi } \approx 0,38H\)
Cơ sở hoạt động của máy biến thế dựa trên hiện tượng:
-
A
Hiện tượng từ trễ
-
B
Cảm ứng từ
-
C
Cảm ứng điện từ
-
D
Cộng hưởng điện từ
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về máy biến thế và hoạt động của máy biến thế
Đặt điện áp xoay chiều tần số f ở hai đầu cuộn sơ cấp. Nó gây ra sự biến thiên từ thông trong hai cuộn.
Gọi từ thông này là: \(\varphi {\rm{ }} = {\rm{ }}{\varphi _0}cos\omega t\)
- Từ thông qua cuộn sơ cấp và thứ cấp lần lượt là : \({\varphi _1} = {N_1}{\varphi _0}cos\omega t\) và \({\varphi _2} = {N_2}{\varphi _0}cos\omega t\)
- Trong cuộn thứ cấp xuất hiện suất điện động cảm ứng e2 có biểu thức \({e_2} = - \dfrac{{d\Phi }}{{dt}} = {N_2}\omega {\Phi _0}\sin \omega t\)
Từ đó ta thấy nguyên tắc hoạt động của máy biến áp dựa vào hiện tượng cảm ứng điện từ.
Máy biến thế dùng để:
-
A
Giữ cho hđt luôn ổn định, không đổi
-
B
Giữ cho cường độ dòng điện luôn ổn định, không đổi
-
C
Làm tăng hay giảm cường độ dòng điện
-
D
Làm tăng hay giảm hiệu điện thế
Đáp án của giáo viên lời giải hay : D
Vì máy biến thế là những thiết bị có khả năng biến đổi điện áp (xoay chiều) và không làm thay đổi tần số của nó.
Một máy biến áp, quận sơ cấp có \(200\) vòng, cuộn thứ cấp có \(100\) vòng. Nếu cuộn thứ cấp có hiệu điện thế \(200V\) thì cuộn sơ cấp có hiệu điện thế đầu vào là bao nhiêu?
-
A
100 V
-
B
200 V
-
C
400 V
-
D
500 V
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}\)
Ta có: \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} \to {U_1} = \frac{{{N_1}}}{{{N_2}}}{U_2} = \frac{{200}}{{100}}.200 = 400V\)
Điện áp và cường độ dòng điện ở cuộn sơ cấp là \(220V\) và \(0,5A\) , ở cuộn thứ cấp là \(20{\rm{ }}V\) và \(6,2A\). Biết hệ số công suất ở cuộn sơ cấp bằng \(1\), ở cuộn thứ cấp là \(0,8\). Hiệu suất của máy biến áp là tỉ số giữa công suất của cuộn thứ cấp và của cuộn sơ cấp là?
-
A
\(80\% \)
-
B
\(40\% \)
-
C
\(90,18\% \)
-
D
\(95\% \)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính công suất: \(P = UI\cos \varphi \)
Ta có hiệu suất máy biến áp là tỉ số giữa công suất của cuộn thứ cấp và cuộn sơ cấp nên:
\(H = \frac{{{P_2}}}{{{P_1}}} = \frac{{{U_2}{I_2}\cos {\varphi _2}}}{{{U_1}{I_1}\cos {\varphi _1}}} = \frac{{20.6,2.0,8}}{{220.0,5.1}} = 0,9018 = 90,18\% \)
Người ta truyền tải điện xoay chiều một pha từ một trạm phát điện cách nơi tiêu thụ \(10km\). Dây dẫn làm bằng kim loại có điện trở suất \({2,5.10^{ - 8}}\Omega .m\), tiết diện \(0,4c{m^2}\), hệ số công suất của mạch điện là \(0,9\). Điện áp và công suất truyền đi ở trạm phát điện là \(10{\rm{ }}kV\) và \(500{\rm{ }}kW\). Hiệu suất truyền tải điện là:
-
A
\(93,75\% \)
-
B
\(96,88\% \)
-
C
\(92,28\% \)
-
D
\(96,14\% \)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính điện trở; \(R = \rho \dfrac{l}{S}\)
+ Sử dụng biểu thức tính công suất hao phí: \(\Delta P = \dfrac{{{P^2}}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\)
+ Hiệu suất truyền tải điện năng: \(H = \dfrac{{P - \Delta P}}{P}\)
+ Ta có : \(l = 2d = 20000{\rm{ }}m{\rm{ }},{\rm{ }}\rho = {2,5.10^{ - 8}}\Omega .m{\rm{ }},S = {4.10^{ - 5}}m\)
+ \(R = \rho \dfrac{l}{S} = {2,5.10^{ - 8}}\dfrac{{20000}}{{{{4.10}^{ - 5}}}} = 12,5\Omega \)
+ Công suất hao phí là: \(\Delta P = \dfrac{{{P^2}}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}R\)
=> Hiệu suất truyền tải điện là:
\(\begin{array}{l}H = \dfrac{{P - \Delta P}}{P} = 1 - \dfrac{{\Delta P}}{P}\\ = 1 - \dfrac{P}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }} = 1 - \dfrac{{{{500.10}^3}}}{{{{\left( {{{10.10}^3}.0,9} \right)}^2}}}\\ = 0,9228 = 92,28\% \end{array}\)
Người ta tính toán rằng khi truyền tải điện năng đi xa với công suất truyền đi, hệ số công suất và công suất hao phí trên đường dây không đổi, nếu tăng điện áp nơi truyền lên \(2,5\) lần thì tiết diện dây dẫn (làm bằng cùng một chất liệu) sử dụng so với ban đầu:
-
A
giảm \(6,25\) lần
-
B
tăng \(6,25\) lần
-
C
giảm \(2,5\) lần
-
D
tăng \(2,5\) lần
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính công suất hao phí: \(\Delta P = \frac{{{P^2}}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\)
+ Sử dụng biểu thức tính điện trở; \(R = \rho \frac{l}{S}\)
+ Ta có: \(\Delta P = \frac{{{P^2}}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}R\)
Vì công suất truyền đi, hệ số công suất và công suất hao phí trên đường dây không đổi nên khi tăng điện áp nơi truyền lên \(2,5\) lần thì \(R' = 6,25{\rm{ }}R\)
Mà \(R = \rho \frac{l}{S}\)
Ta suy ra: \(S' = \frac{S}{{6,25}}\)
=> tiết diện dây dẫn giảm \(6,25\) lần
Đặt điện áp \(u = U\sqrt 2 {\rm{cos2}}\pi {\rm{ft}}\) (trong đó u tính bằng V, t tính bằng s, U không đổi còn f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần \(R\) và tụ có điện dung \(C\) mắc nối tiếp. Khi \(f{\rm{ }} = {\rm{ }}{f_1} = {\rm{ }}20Hz\) thì công suất tiêu thụ trên đoạn mạch là \(10,0W\). Khi \(f{\rm{ }} = {\rm{ }}{f_2} = {\rm{ }}40Hz\) thì công suất tiêu thụ trên đoạn mạch là \(20,0W\) . Khi \(f{\rm{ }} = {\rm{ }}{f_3} = {\rm{ }}60Hz\) thì công suất tiêu thụ trên đoạn mạch là :
-
A
\(40,0W\)
-
B
\(30,0W\)
-
C
\(20,77W\)
-
D
\(28,9W\)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính công suất: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ Khi \(f = {f_1}\) thì \(P = \dfrac{{{U^2}.R}}{{\left( {{R^2}{\rm{ }} + {\rm{ }}{Z^2_C}} \right)}} = 10\left( 1 \right)\)
+ Khi \(f = {f_2} = 2{f_1}\) thì \(P{\rm{ }} = \frac{{{U^2}.R}}{{\left( {{R^2}{\rm{ }} + {\rm{ }}\dfrac{{{Z_C}^2}}{4}} \right)}} = 20\left( 2 \right)\)
+ Khi \(f = {f_3} = 3{f_1}\) thì \(P = \frac{{{U^2}.R}}{{\left( {{R^2}{\rm{ }} + {\rm{ }}\frac{{Z_C^2}}{9}} \right)}}\left( 3 \right)\)
Lấy \(\frac{{\left( 1 \right)}}{{(2)}}\) ta được : \({Z_C}^2 = 2{R^2}\left( 4 \right)\)
Từ (1) $ \to {U^2}.R = 10\left( {{R^2} + {Z_C}^2} \right)\left( 5 \right)$
Thế (4) và (5) vào (3) ta được: \(P = 20,77W\)
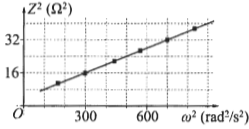
Trong giờ thực hành đo độ tự cảm của một cuộn dây, học sinh mắc nối tiếp cuộn dây đó với một điện trở thành một đoạn mạch. Đặt điện áp xoay chiều có tần số góc \(\omega \) thay đổi được vào hai đầu đoạn mạch rồi đo tổng trở Z của đoạn mạch. Hình bên là đồ thị biểu diễn sự phụ thuộc của \({Z^2}\) theo \({\omega ^2}.\) Độ tự cảm của cuộn dây bằng
-
A
0,1 H.
-
B
0,01 H.
-
C
0,2 H.
-
D
0,04 H.
Đáp án của giáo viên lời giải hay : C
Cảm kháng của cuộn dây: \({Z_L} = \omega L\)
Tổng trở của mạch: \(Z = \sqrt {{R^2} + {Z_L}^2} = \sqrt {{R^2} + {\omega ^2}{L^2}} \)
Sử dụng kĩ năng đọc đồ thị
Từ đồ thị ta thấy với \(\left\{ \begin{array}{l}{Z^2} = 32\left( {{\Omega ^2}} \right) \Rightarrow {\omega ^2} = 700\left( {ra{d^2}/{s^2}} \right)\\{Z^2} = 16\left( {{\Omega ^2}} \right) \Rightarrow {\omega ^2} = 300\,\,\left( {ra{d^2}/{s^2}} \right)\end{array} \right.\)
Mà \({Z^2} = {R^2} + {\omega ^2}{L^2}\)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}16 = {R^2} + 300{L^2}\\32 = {R^2} + 700{L^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 2\left( \Omega \right)\\L = 0,2\left( H \right)\end{array} \right.\)
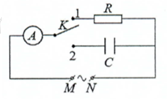
Trong giờ thực hành, để đo điện dung C của một tụ điện, một học sinh mắc mạch điện theo sơ đồ như hình bên. Đặt vào hai đầu M, N một điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số 50 Hz. Khi đóng khóa K vào chốt 1 thì số chỉ của ampe kế A là I. Chuyển khóa K sang chốt 2 thì số chỉ của ampe kế A là 2I. Biết R = 680 Ω. Bỏ qua điện trở của ampe kế và dây nối. Giá trị của C là
-
A
\(9,{36.10^{ - 6}}\,\,F\)
-
B
\(4,{68.10^{ - 6}}\,\,F\)
-
C
\(18,{73.10^{ - 6}}\,\,F\)
-
D
\(2,{34.10^{ - 6}}\,\,F\)
Đáp án của giáo viên lời giải hay : A
Cường độ dòng điện trong mạch: \(\left\{ \begin{array}{l}{I_1} = \dfrac{U}{R}\\{I_2} = \dfrac{U}{{{Z_C}}}\end{array} \right.\)
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{2\pi C}}\)
Cường độ dòng điện khi khóa K ở vị trí 1 và 2 là:
\(\left\{ \begin{array}{l}{I_1} = I = \dfrac{U}{R}\\{I_2} = 2I = \dfrac{U}{{{Z_C}}}\end{array} \right. \Rightarrow \dfrac{1}{2} = \dfrac{{{Z_C}}}{R} \Rightarrow {Z_C} = \dfrac{R}{2} = \dfrac{{680}}{2} = 340\,\,\left( \Omega \right)\)
Dung kháng của tụ điện là:
\({Z_C} = \dfrac{1}{{2\pi fC}} \Rightarrow 340 = \dfrac{1}{{2\pi .50.C}} \Rightarrow C = 9,{36.10^{ - 6}}\,\,\left( F \right)\)
Đặt điện áp xoay chiều có giá trị hiệu dụng 220 V vào hai đầu đoạn mạch AB như hình bên. Biết điện áp tức thời uAM và uMB lệch pha nhau \(\dfrac{\pi }{3}\), điện áp tức thời uAB và uMB lệch pha nhau \(\dfrac{\pi }{6}.\) Điện áp hiệu dụng hai đầu đoạn mạch AM là
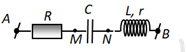
-
A
110 V.
-
B
113,1 V.
-
C
138,6 V.
-
D
127 V.
Đáp án của giáo viên lời giải hay : D
Sử dụng giản đồ vecto và định lí hàm sin: \(\dfrac{a}{{\sin \widehat A}} = \dfrac{b}{{\sin \widehat B}} = \dfrac{c}{{\sin \widehat C}}\)
Ta có giản đồ vecto:
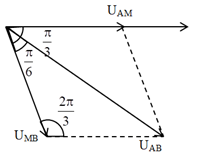
Từ giản đồ vecto, ta có định lí hàm sin:
\(\dfrac{{{U_{AB}}}}{{\sin \dfrac{{2\pi }}{3}}} = \dfrac{{{U_{AM}}}}{{\sin \dfrac{\pi }{6}}} \Rightarrow {U_{AM}} = \dfrac{{{U_{AB}}\sin \dfrac{\pi }{6}}}{{\sin \dfrac{{2\pi }}{3}}} = \dfrac{{220\sin \dfrac{\pi }{6}}}{{\sin \dfrac{{2\pi }}{3}}} = 127\,\,\left( V \right)\)
Đặt điện áp xoay chiều \(u = {U_0}\cos \left( {100\pi t - \dfrac{\pi }{2}} \right)\,\,\left( V \right)\) (t đo bằng giây) vào hai đầu đoạn mạch nối tiếp gồm tụ điện có điện dung \(C = \dfrac{{0,2}}{\pi }\,\,\left( {mF} \right)\) và điện trở thuần \(R = 50\,\,\Omega \). Sau thời điểm ban đầu (t = 0) một khoảng thời gian ngắn nhất bằng bao nhiêu thì điện tích trên tụ điện bằng 0?
-
A
12,5 ms
-
B
2,5 ms
-
C
25 μs
-
D
750 μs
Đáp án của giáo viên lời giải hay : B
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\)
Độ lệch pha giữa điện áp và cường độ dòng điện: \(\tan \varphi = \dfrac{R}{{ - {Z_C}}}\)
Điện tích trên tụ điện: q = C.u
Giải phương trình lượng giác để tìm t.
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{0,{{2.10}^{ - 3}}}}{\pi }}} = 50\,\,\left( \Omega \right)\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch với cường độ dòng điện là:
\(\begin{gathered}
\tan \varphi = \frac{R}{{ - {Z_C}}} = \frac{{50}}{{ - 50}} \Rightarrow \varphi = - \frac{\pi }{4} = {\varphi _u} - {\varphi _i} \hfill \\
\Rightarrow {\varphi _i} = {\varphi _u} - \varphi = - \frac{\pi }{2} - \left( { - \frac{\pi }{4}} \right) = - \frac{\pi }{4}{\mkern 1mu} {\mkern 1mu} \left( {rad} \right) \hfill \\
\end{gathered} \)
Nhận xét: Dòng điện sớm pha hơn điện áp giữa hai đầu tụ điện → pha ban đầu của điện áp giữa hai đầu tụ điện là: \({\varphi _{{u_C}}} = {\varphi _i} - \dfrac{\pi }{2} = - \dfrac{\pi }{4} - \dfrac{\pi }{2} = - \dfrac{{3\pi }}{4}\)
Biểu thức điện áp giữa hai đầu tụ điện là:
\({u_C} = {U_{0C}}\cos \left( {100\pi t - \dfrac{{3\pi }}{4}} \right)\,\,\left( V \right)\)
Điện tích trên tụ điện bằng 0 khi điện áp giữa hai đầu tụ điện bằng 0:
\(\begin{gathered}
{u_C} = {U_{0C}}\cos \left( {100\pi t - \frac{{3\pi }}{4}} \right) = 0 \hfill \\
\Rightarrow 100\pi t - \frac{{3\pi }}{4} = - \frac{\pi }{2} \hfill \\
\Rightarrow t = {2,5.10^{ - 3}}{\mkern 1mu} {\mkern 1mu} \left( s \right) = 2,5{\mkern 1mu} {\mkern 1mu} \left( {ms} \right) \hfill \\
\end{gathered} \)
