Đặt điện áp \(u{\rm{ }} = {\rm{ }}{U_0}cos(\omega t)\) vào hai đầu điện trở thuần thì cường độ dòng điện qua R là:
-
A
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{R}cos\left( {\omega t} \right)\)
-
B
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\sqrt 2 R}}cos\left( {\omega t} \right)\)
-
C
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{R}cos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
-
D
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\sqrt 2 R}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
Đáp án của giáo viên lời giải hay : A
Ta có:
+ uR luôn luôn cùng pha với i
+ cường độ dòng điện cực đại:
\({I_0} = \frac{{{U_0}}}{R}\)
=> Biểu thức cường độ dòng điện qua R là:
\(i{\rm{ }} = {\rm{ }}\frac{{{U_0}}}{R}cos\left( {\omega t} \right)\)
Đặt điện áp \(u{\rm{ }} = {\rm{ }}{U_0}cos(\omega t)\) vào hai đầu cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện qua cuộn cảm thuần là:
-
A
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
-
B
\(i{\rm{ }} = {U_0}{\rm{ }}\omega Lcos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
-
C
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
-
D
\(i{\rm{ }} = {U_0}{\rm{ }}\omega Lcos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
Đáp án của giáo viên lời giải hay : C
Ta có:
+ uL nhanh pha hơn i một góc \(\dfrac{\pi }{2}\)
+ Cường độ dòng điện cực đại:
\({I_0} = \dfrac{{{U_0}}}{{{Z_L}}} = \dfrac{{{U_0}}}{{\omega L}}\)
=> Biểu thức cường độ dòng điện qua cuộn cảm thuần là:
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
Đặt điện áp u = U0cos(ωt) vào hai đầu tụ điện có điện dung C thì cường độ dòng điện qua tụ là:
-
A
\(i{\rm{ }} = {U_0}\omega Ccos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
-
B
\(i{\rm{ }} = {U_0}\omega Ccos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
-
C
\(i{\rm{ }} = \dfrac{{{U_0}}}{{\omega C}}cos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
-
D
\(i{\rm{ }} = \dfrac{{{U_0}}}{{\omega C}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
Đáp án của giáo viên lời giải hay : A
+ uC chậm pha hơn i một góc: \(\dfrac{\pi }{2}\)
+ Sử dụng biểu thức tính cường độ dòng điện cực đại: \({I_0} = \dfrac{{{U_0}}}{{{Z_C}}}\)
Ta có:
+ uC chậm pha hơn i một góc: \(\dfrac{\pi }{2}\)
+ Cường độ dòng điện cực đại: \({I_0} = \dfrac{{{U_0}}}{{{Z_C}}} = \dfrac{{{U_0}}}{{\frac{1}{{\omega C}}}} = {U_0}\omega C\)
=> Biểu thức cường độ dòng điện qua tụ điện là:
\(i{\rm{ }} = {U_0}\omega Ccos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
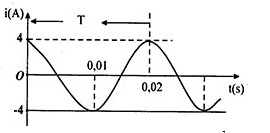
Đồ thị cường độ dòng điện như hình vẽ
Cường độ dòng điện tức thời có biểu thức
-
A
\(i = 4c{\rm{os}}\left( {100\pi t + \frac{\pi }{2}} \right)A\)
-
B
\(i = 4c{\rm{os}}\left( {100\pi t + \frac{{3\pi }}{2}} \right)A\)
-
C
\(i = 4c{\rm{os}}\left( {100\pi t} \right)A\)
-
D
\(i = 4c{\rm{os}}\left( {50\pi t + \frac{\pi }{2}} \right)A\)
Đáp án của giáo viên lời giải hay : C
Đọc đồ thị cường độ dòng điện theo thời gian
Từ đồ thị ta có:
+ Chu kì:
\(T = 0,02{\rm{s}} \to \omega {\rm{ = }}\frac{{2\pi }}{T} = 100\pi (ra{\rm{d}}/s)\)
+ Cường độ dòng điện cực đại:
\({I_0} = 4(A)\)
+ Tại t = 0:
\(i = 4 \leftrightarrow {I_0}{\rm{cos}}\varphi {\rm{ = 4}} \to c{\rm{os}}\varphi {\rm{ = 1}} \to \varphi {\rm{ = 0}}\)
=> Biểu thức cường độ dòng điện tức thời:
\(i = 4c{\rm{os}}\left( {100\pi t} \right)A\)
Mạch chỉ có R, biểu thức i qua mạch có dạng \(i = 2cos100\pi t(A),{\rm{ }}R = 20\Omega \) , viết biểu thức u?
-
A
\(u{\rm{ }} = {\rm{ }}40cos(100\pi t + \frac{\pi }{2}){\rm{ }}V\)
-
B
\(u{\rm{ }} = {\rm{ }}40\sqrt 2 cos(100\pi t + {\rm{ }}\pi /2){\rm{ }}V\)
-
C
\(u{\rm{ }} = {\rm{ }}40cos(100\pi t){\rm{ }}V\)
-
D
\(u{\rm{ }} = {\rm{ }}40\sqrt 2 cos(100pt + {\rm{ }}\pi ){\rm{ }}V\)
Đáp án của giáo viên lời giải hay : C
Ta có: \(u = iR = 40cos\left( {100\pi t} \right){\rm{ }}\left( V \right)\)
Mạch điện chỉ có cuộn cảm thuần, L= 1/π H, biểu thức dòng điện trong mạch có dạng i = 2cos(100πt) A. Tính cảm kháng trong mạch ZL và viết biểu thức hiệu điện thế hai đầu mạch điện?
-
A
\({Z_L} = 100{\rm{ }}\Omega ;{\rm{ }}u = 200cos(100\pi t - \frac{\pi }{2}){\rm{ }}V\)
-
B
\({Z_L} = 100\Omega ;u = 200cos(100\pi t + {\rm{ }}\frac{\pi }{2}){\rm{ }}V\)
-
C
\({Z_L} = 100{\rm{ }}\Omega ;{\rm{ }}u = 200cos(100\pi t){\rm{ }}V\)
-
D
\({Z_L} = 200{\rm{ }}\Omega ;{\rm{ }}u = 200cos(100\pi t + {\rm{ }}\frac{\pi }{2}){\rm{ }}V\)
Đáp án của giáo viên lời giải hay : B
+ Đọc phương trình cường độ dòng điện
+ Áp dụng công thức tính cảm kháng : \({Z_L} = \omega L\)
Ta có:
+ Cảm kháng:
\({Z_L} = \omega L = 100\pi .\frac{1}{\pi } = 100\Omega \)
\({U_0} = {\text{ }}{I_0}.{Z_L} = {\text{ }}2.100{\text{ }} = {\text{ }}200V\)
u sớm pha hơn i góc π/2
\( = > u = 200cos(100\pi t + {\rm{ }}\frac{\pi }{2}){\rm{ }}V\)
Đồ thị biểu diễn cường độ tức thời của dòng điện xoay chiều chỉ có cuộn cảm thuần có cảm kháng \(Z_L=50\Omega\) như hình sau:
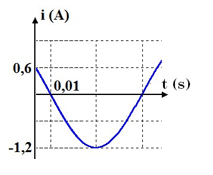
Viết biểu thức điện áp tức thời giữa hai đầu cuộn cảm.
-
A
\(u = 60c{\rm{os(}}\dfrac{{50\pi t}}{3} + \dfrac{4\pi }{3})\)
-
B
\(u = 60\sin {\rm{(}}\dfrac{{50\pi t}}{3} + \dfrac{4\pi }{3})\)
-
C
\(u = 60c{\rm{os(}}\dfrac{{50\pi t}}{3} + \dfrac{\pi }{6})\)
-
D
\(u = 30c{\rm{os(}}\dfrac{{50\pi t}}{3} + \dfrac{\pi }{3})\)
Đáp án của giáo viên lời giải hay : B
+ Đọc đồ thị cường độ dòng điện theo thời gian
+ Sử dụng công thức lượng giác: \({\rm{cos}}\left( x \right) = \sin \left( {x + \frac{\pi }{2}} \right)\)
Từ đồ thị ta có:
\(\dfrac{T}{{12}} = 0,01{\rm{s}} \to T = 0,12{\rm{s}} \\\to \omega {\rm{ = }}\dfrac{{2\pi }}{T} = \dfrac{{50\pi }}{3}(ra{\rm{d}}/s)\)
+ Cường độ dòng điện cực đại:
\({I_0} = 1,2(A)\)
+ Tại \(t = 0\): \(i = 0,6A\) và đang giảm:
\(i = 0,6 \leftrightarrow {I_0}{\rm{cos}}\varphi {\rm{ = 0}}{\rm{,6}} \\\to c{\rm{os}}\varphi {\rm{ = }}\dfrac{{0,6}}{{1,2}} = \dfrac{1}{2} \to \varphi {\rm{ = }}\dfrac{\pi }{3}\)
=> Biểu thức cường độ dòng điện tức thời:
\(i = 1,2c{\rm{os}}\left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3}} \right)A\)
+ Ta có uL nhanh pha hơn i một góc \(\dfrac{\pi }{2}\)
+ Hiệu điện thế cực đại:
\({U_0} = {I_0}.{Z_L} = 1,2.50 = 60(V)\)
=> Biểu thức điện áp tức thời giữa hai đầu cuộn cảm:
$u = 60c{\rm{os}}\left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) \\= 60\sin \left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3} + \dfrac{\pi }{2} + \dfrac{\pi }{2}} \right) \\= 60\sin \left( {\dfrac{{50\pi }}{3}t + \dfrac{{4\pi }}{3}} \right)V$
Mạch điện gồm cuộn dây thuần cảm, độ tự cảm \(L{\rm{ }} = \dfrac{1}{{4\pi }}{\rm{ }}H\) được gắn vào mạng điện xoay chiều người ta thấy dòng điện trong mạch có biểu thức là \(i = 2{\rm{ }}cos(100\pi t - \dfrac{\pi }{6}){\rm{ }}A\) . Hỏi nếu gắn vào mạng điện đó đoạn mạch chỉ có tụ điện có điện dung là \(\dfrac{{{{10}^{ - 3}}}}{{2\pi }}\) thì dòng điện trong mạch có biểu thức là?
-
A
\(i = 25cos\left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
B
\(i = 2,5cos\left( {100\pi t + \dfrac{\pi }{6}} \right)A\)
-
C
\(i = 2,5cos\left( {100\pi t + \dfrac{{5\pi }}{6}} \right)A\)
-
D
\(i = 0,25cos\left( {100\pi t + \dfrac{{5\pi }}{6}} \right)A\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Sử dụng biểu thức tính hiệu điện thế cực đại
Theo đầu bài, ta có hiệu điện thế hai đầu đoạn mạch không thay đổi
+ Khi mạch chỉ có L thì cường độ dòng điện cực đại trong mạch là: \({I_{01}} = 2A\)
+ Khi mạch chỉ có C thì cường độ dòng điện cực đại trong mạch là: \({I_{02}}\)
Mặt khác, ta có: \(\left\{ \begin{array}{l}{I_{01}} = \dfrac{{{U_0}}}{{{Z_L}}}\\{I_{02}} = \dfrac{{{U_0}}}{{{Z_C}}}\end{array} \right.\)
Từ đó ta suy ra: \(\dfrac{{{I_{01}}}}{{{I_{02}}}} = \dfrac{{{Z_C}}}{{{Z_L}}}\)
Lại có: \(\left\{ \begin{array}{l}{Z_L} = \omega L = 25\Omega \\{Z_C} = \dfrac{1}{{\omega C}} = 20\Omega \end{array} \right.\)
Từ đấy ta suy ra: \(\dfrac{{{I_{01}}}}{{{I_{02}}}} = \dfrac{{{Z_C}}}{{{Z_L}}} = \dfrac{{20}}{{25}} = 0,8 \to {I_{02}} = \dfrac{{{I_{01}}}}{{0,8}} = 2,5A\)
Khi mạch có L, u sớm pha hơn i góc \(\dfrac{\pi }{2} \to {\varphi _u} = {\varphi _{{i_1}}} + \dfrac{\pi }{2}\)
Khi mạch có C, u trễ pha hơn i góc \(\dfrac{\pi }{2} \to {\varphi _{{i_2}}} = {\varphi _u} + \dfrac{\pi }{2} = {\varphi _{{i_1}}} + \dfrac{\pi }{2} + \dfrac{\pi }{2} = \dfrac{{5\pi }}{6}\)
=> \({i_2} = 2,5cos\left( {100\pi t + \dfrac{{5\pi }}{6}} \right)A\)
Mạch điện xoay chiều chỉ chứa tụ điện \(C = \frac{1}{{7200\pi }}{\rm{ }}F\) , hiệu điện thế xoay chiều ổn định đặt vào hai đầu mạch là \(u = {U_0}cos\left( {\omega t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V\) . Tại thời điểm t1 ta có \({u_1} = 60\sqrt 2 {\rm{ }}V\) và \({i_1} = \frac{{\sqrt 2 }}{2}A\) , tại thời điểm t2 ta có \({u_2} = - {\rm{ }}60\sqrt 3 {\rm{ }}V\) và và \({i_2} = - 0,5A\) . Hãy hoàn thiện biểu thức của điện áp u.
-
A
\(u{\rm{ }} = 120cos\left( {100{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V\)
-
B
\(u{\rm{ }} = 60cos\left( {120{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V\)
-
C
\(u{\rm{ }} = 60cos\left( {50{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V\)
-
D
\(u = 120cos\left( {60{\rm{ }}\pi {\rm{ }}t{\rm{ }} + {\rm{ }}\frac{\pi }{4}{\rm{ }}} \right){\rm{ }}V\)
Đáp án của giáo viên lời giải hay : D
Vận dụng biểu thức: \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Do mạch chỉ có C nên: \(u \bot i \to \frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Thay các giá trị, ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\frac{{{{(60\sqrt 2 )}^2}}}{{U_0^2}} + \frac{{{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}}}{{I_0^2}} = 1{\rm{ (1)}}\\\frac{{{{\left( {60\sqrt 3 } \right)}^2}}}{{U_0^2}} + \frac{{{{\left( {0,5} \right)}^2}}}{{I_0^2}} = 1{\rm{ (2)}}\end{array} \right.\\ \to \frac{{3600}}{{U_0^2}} = \frac{{0,25}}{{I_0^2}} \to \frac{{{U_0}}}{{{I_0}}} = 120 = {Z_C}\end{array}\)
Lại có, \({Z_C} = \frac{1}{{\omega C}} \to \omega = \frac{1}{{{Z_C}C}} = \frac{1}{{120.C}} = \frac{1}{{120.\frac{1}{{7200\pi }}}} = 60\pi \)
Thay \({I_0} = \frac{{{U_0}}}{{120}}\) vào (1) , ta được: \(\frac{{{{(60\sqrt 2 )}^2}}}{{U_0^2}} + \frac{{{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}}}{{\frac{{U_0^2}}{{{{120}^2}}}}} = 1 \to {U_0} = 120(V)\)
\( \to u = 120cos\left( {60{\rm{ }}\pi {\rm{ }}t{\rm{ }} + {\rm{ }}\frac{\pi }{4}{\rm{ }}} \right){\rm{ }}V\)
Đặt điện áp \(u{\rm{ }} = {U_0}cos(100{\rm{ }}\pi t{\rm{ }}-\pi /3){\rm{ }}V\) vào hai đầu một tụ điện có điện dung \(\frac{{{{2.10}^{ - 4}}}}{\pi }{\rm{ }}F\) . Ở thời điểm điện áp giữa hai đầu tụ điện là 150 V thì cường độ dòng điện trong mạch là 4A. Biểu thức của cường độ dòng điện trong mạch là:
-
A
\(i{\rm{ }} = 4\sqrt 2 cos(100\pi t + \pi /6){\rm{ }}A\)
-
B
\(i{\rm{ }} = {\rm{ }}5cos(100\pi t{\rm{ }} + \pi /6){\rm{ }}A\)
-
C
\(i{\rm{ }} = {\rm{ }}4\sqrt 2 cos(100\pi t{\rm{ }} - \pi /6){\rm{ }}A\)
-
D
\(i{\rm{ }} = {\rm{ }}5cos(100\pi t{\rm{ }} - \pi /6)A\)
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức: \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Do mạch chỉ có C nên:
\(u \bot i \to \frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Lại có:
\({U_0} = {I_0}{Z_C}\)
\( \to \frac{{{{150}^2}}}{{{{(50.{I_0})}^2}}} + \frac{{{4^2}}}{{I_0^2}} = 1 \to {I_0} = 5(A)\)
Ta có i sớm pha hơn uC một góc: \(\frac{\pi }{2}\)
$ \to {\varphi _i} = \frac{\pi }{2} + \left( { - \frac{\pi }{3}} \right) = \frac{\pi }{6}$
\( \to i{\rm{ }} = {\rm{ }}5cos(100\pi t{\rm{ }} + \frac{\pi }{6}){\rm{ }}A\)
Đặt điện áp xoay chiều \(u{\rm{ }} = {U_0}cos(100{\rm{ }}\pi t{\rm{ }}-\pi /3){\rm{ }}V\) vào hai đầu một cuộn cảm thuần có độ tự cảm \(\frac{1}{{2\pi }}{\rm{ }}H\) . Ở thời điểm điện áp giữa hai đầu cuộn cảm là \(100\sqrt 2 {\rm{ }}V\) thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là
-
A
\(i{\rm{ }} = {\rm{ }}2\sqrt 3 cos(100\pi t{\rm{ }} - 5\pi /6){\rm{ }}A\)
-
B
\(i{\rm{ }} = 2\sqrt 3 cos(100\pi t{\rm{ }} + \frac{\pi }{6}){\rm{ }}A\)
-
C
\(i{\rm{ }} = 2cos(100\pi t + \frac{\pi }{6}){\rm{ }}A\)
-
D
\(i{\rm{ }} = {\rm{ }}2\sqrt 2 cos(100\pi t{\rm{ }} - \frac{\pi }{6}){\rm{ }}A\)
Đáp án của giáo viên lời giải hay : A
Vận dụng biểu thức: \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Do mạch chỉ có cuộn dây nên:
\(u \bot i \to \frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Ta có: \({Z_L} = {\text{ }}\omega L{\text{ }} = {\text{ }}50\Omega \to {U_0} = {\text{ }}50{\text{ }}{I_0}\)
\( \to \frac{{{{(100\sqrt 2 )}^2}}}{{{{(50{I_0})}^2}}} + \frac{{{2^2}}}{{I_0^2}} = 1 \to {I_0} = 2\sqrt 3 (A)\)
Mạch có cuộn dây nên i chậm pha hơn u góc \(\frac{\pi }{2}{\text{ }}\)
\(\to {\varphi _{i}} = - 5\pi /6\)
$ \to i = 2\sqrt 3 {\rm{cos(100}}\pi {\rm{t - }}\frac{{5\pi }}{6})(A)$
Một đoạn mạch điện xoay chiều gồm \(R{\rm{ }} = {\rm{ }}60{\rm{ }}\Omega \) , cuộn cảm thuần \(L = \dfrac{{0,2}}{\pi }H\) và \(C{\rm{ }} = \dfrac{{{{10}^{ - 3}}}}{{8\pi }}F\) mắc nối tiếp. Điện áp giữa hai đầu đoạn mạch là \(u = 100\sqrt 2 cos100\pi tV\). Tìm độ lệch pha giữa điện áp giữa hai đầu đoạn mạch và dòng điện trong mạch?
-
A
\(\dfrac{\pi}{4}\)
-
B
\( -\dfrac{\pi}{4}\)
-
C
\(\dfrac{\pi}{6}\)
-
D
\( -\dfrac{\pi}{6}\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Ta có:
\({Z_L} = \omega L = 100\pi \dfrac{{0,2}}{\pi } = 20\Omega \)
\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 3}}}}{{8\pi }}}} = 80\Omega \)
Độ lệch pha giữa điện áp và cường độ dòng điện trong mạch:
\(\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{20 - 80}}{{60}} = - 1\\ \to \varphi = - \dfrac{\pi }{4}\end{array}\)
Một mạch điện gồm R = 60 Ω, cuộn cảm thuần có độ tự cảm L = 0,4/π H và tụ điện có điện dung C = 10-4/π F mắc nối tiếp, biết f = 50 Hz tính tổng trở trong mạch và độ lệch pha giữa u và i?
-
A
60 Ω; π /4 rad
-
B
60 $\sqrt 2 $ Ω; π /4 rad
-
C
60 $\sqrt 2 $ Ω; - π /4 rad
-
D
60 Ω; - π /4 rad
Đáp án của giáo viên lời giải hay : C
$Zc = \frac{1}{{2\pi fC}} = 100\Omega ;{Z_L} = 40\Omega $
$Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{{60}^2} + {{(40 - 100)}^2}} = 60\sqrt 2 $
$\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = - 1 \to \varphi = - \frac{\pi }{4}$
Đặt điện áp xoay chiều vào hai đầu đoạn mạch $R, L, C$ mắc nối tiếp. Biết $R = 10\Omega $, cuộn cảm thuần có hệ số tự cảm \(L = \dfrac{1}{{10\pi }}H\) , tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 3}}}}{{2\pi }}H\)và điện áp giữa hai đầu cuộn cảm thuần là \({u_L} = 20\sqrt 2 {\rm{cos(100}}\pi {\rm{t + }}\dfrac{\pi }{4})(V)\) . Biểu thức điện áp giữa hai đầu đoạn mạch là:
-
A
\(u = 40c{\rm{os(100}}\pi {\rm{t + }}\dfrac{\pi }{4})(V)\)
-
B
\(u = 40c{\rm{os(100}}\pi {\rm{t - }}\dfrac{\pi }{2})(V)\)
-
C
\(u = 40\sqrt 2 c{\rm{os(100}}\pi {\rm{t + }}\dfrac{\pi }{4})(V)\)
-
D
\(u = 40\sqrt 2 c{\rm{os(100}}\pi {\rm{t - }}\dfrac{\pi }{2})(V)\)
Đáp án của giáo viên lời giải hay : B
- Cách 1:
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Vận dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
- Cách 2: Sử dụng máy tính
- Cách 1
Ta có:
+ Cảm kháng: \({Z_L} = \omega L = 100\pi \dfrac{1}{{10\pi }} = 10\Omega \)
+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi \dfrac{{{{10}^{ - 3}}}}{{2\pi }}}} = 20\Omega \)
+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{10}^2} + {{\left( {10 - 20} \right)}^2}} = 10\sqrt 2 \Omega \)
+ Hiệu điện thế trên hai đầu cuộn cảm: \({U_{0L}} = {I_0}.{Z_L}\)
=> Cường độ dòng điện cực đại của mạch: \({I_0} = \dfrac{{{U_{0L}}}}{{{Z_L}}} = \dfrac{{20\sqrt 2 }}{{10}} = 2\sqrt 2 A\)
=> Hiệu điện thế cực đại: \({U_0} = {I_0}.Z = 2\sqrt 2 .10\sqrt 2 = 40V\)
+ \(\tan {\varphi _{\left( {{u_{AB}},i} \right)}} = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{10 - 20}}{{10}} = - 1\)
Ta suy ra: \(\varphi = - \dfrac{\pi }{4}\)
Mặt khác, ta có:
\(\begin{array}{l}{\varphi _{{u_L}}} - {\varphi _i} = \dfrac{\pi }{2}\\ \Rightarrow {\varphi _i} = {\varphi _{{u_L}}} - \dfrac{\pi }{2} = \dfrac{\pi }{4} - \dfrac{\pi }{2} = - \dfrac{\pi }{4}\end{array}\)
Lại có:
\(\begin{array}{l}{\varphi _{{u_{AB}}}} - {\varphi _i} = - \dfrac{\pi }{4}\\ \Rightarrow {\varphi _{{u_{AB}}}} = {\varphi _i} - \dfrac{\pi }{4} = - \dfrac{\pi }{4} - \dfrac{\pi }{4} = - \dfrac{\pi }{2}\end{array}\)
=> Biểu thức hiệu điện thế giữa hai đầu đoạn mạch: \(u = 40cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V\)
- Cách 2: Sử dụng máy tính
+ Bước 1: MODE 2
+ Bước 2: Chọn chế độ rad: SHIFT MODE 4
+ Bước 3: Nhập liệu
\(\begin{array}{l}\overline {{u_{AB}}} = \overline i .\overline {{Z_{AB}}} = \overline {\dfrac{{{u_L}}}{{{Z_L}}}.} \overline {{Z_{AB}}} \\ = \dfrac{{20\sqrt 2 \angle \dfrac{\pi }{4}}}{{10i}}\left( {10 - 10i} \right)\end{array}\)
+ Bước 4: Gọi kết quả: SHIFT 2 3 =
Kết quả hiển thị trên máy: \(40\angle \dfrac{{ - \pi }}{2}\)
=> Biểu thức hiệu điện thế giữa hai đầu đoạn mạch: \(u = 40cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V\)
Đặt điện áp \(u = {U_0}{\rm{cos100}}\pi {\rm{t}}\left( V \right)\) (t tính bằng s) vào đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm \(L = \dfrac{{1,5}}{\pi }H\), điện trở \(r = 50\sqrt 3 \Omega \), tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 4}}}}{\pi }F\) . Tại thời điểm t1, điện áp tức thời giữa hai đầu cuộn dây có giá trị $150V$, đến thời điểm \({t_1} + \dfrac{1}{{75}}s\) thì điện áp giữa hai đầu tụ điện cũng bằng $150V$. Giá trị của U0 bằng
-
A
\(150\sqrt 3 V\)
-
B
\(100\sqrt 3 V\)
-
C
$300 V$
-
D
$150V$
Đáp án của giáo viên lời giải hay : B
Ta có:
\(\begin{array}{l}{Z_L} = \omega L = 150\Omega ;{Z_C} = \dfrac{1}{{\omega C}} = 100\Omega ;r = 50\sqrt 3 \Omega \\Z = 100\Omega ;{Z_d} = \sqrt {{r^2} + {Z_L}^2} = 100\sqrt 3 \end{array}\)
\(\begin{array}{l}i = \dfrac{{{U_0}}}{Z}{\rm{cos}}\left( {\omega t - \dfrac{\pi }{6}} \right) = 0,01{U_0}{\rm{cos}}\left( {\omega t - \dfrac{\pi }{6}} \right)\\{u_d} = {I_0}{{\rm{Z}}_d}{\rm{cos}}\left( {\omega t + \dfrac{\pi }{6}} \right) = {U_0}\sqrt 3 {\rm{cos}}\left( {\omega t + \dfrac{\pi }{6}} \right)\\{u_C} = {I_0}{Z_C}{\rm{cos}}\left( {\omega t - \dfrac{{2\pi }}{3}} \right) = {U_0}{\rm{cos}}\left( {\omega t - \dfrac{{2\pi }}{3}} \right)\end{array}\)
\({u_d} = {U_0}\sqrt 3 {\rm{cos}}\left( {\omega {t_1} + \dfrac{\pi }{6}} \right) = 150V{\rm{ (1)}}\)
Tại thời điểm
\({t_2} = {t_1} + \dfrac{1}{{75}}s\) , ta có:
\({u_C} = {U_0}{\rm{cos}}\left( {\omega \left( {{t_1} + \dfrac{1}{{75}}} \right) - \dfrac{{2\pi }}{3}} \right) = {U_0}{\rm{cos}}\left( {\omega {t_1} + \dfrac{{2\pi }}{3}} \right) = {U_0}\sin \left( {\omega {t_1} + \dfrac{7\pi }{6}} \right) = 150V{\rm{ (2)}}\)
Từ (1) và (2), ta có:
\(\begin{array}{l}{\left( {\dfrac{{{u_d}}}{{\sqrt 3 }}} \right)^2} + {\left( {{u_C}} \right)^2} = U_0^2 \leftrightarrow \dfrac{{{{150}^2}}}{3} + {150^2} = U_0^2\\ \to {U_0} = 100\sqrt 3 \end{array}\)
Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm \(\frac{1}{{4\pi }}\) H thì dòng điện trong đoạn mạch là dòng điện một chiều có cường độ 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp \(u = 150\sqrt 2 {\rm{cos(120}}\pi {\rm{t)}}\) thì biểu thức của cường độ dòng điện trong đoạn mạch là:
-
A
\(i = 5c{\rm{os(120}}\pi {\rm{t + }}\frac{\pi }{4})A\)
-
B
\(i = 5c{\rm{os(120}}\pi {\rm{t - }}\frac{\pi }{4})A\)
-
C
\(i = 5\sqrt 2 c{\rm{os(120}}\pi {\rm{t + }}\frac{\pi }{4})A\)
-
D
\(i = 5\sqrt 2 c{\rm{os(120}}\pi {\rm{t - }}\frac{\pi }{4})A\)
Đáp án của giáo viên lời giải hay : B
Vận dụng các công thức trong giải điện xoay chiều.
- Cường độ dòng điện một chiều:
\(I = \frac{U}{R}\) ( Khi cho dòng điện 1 chiều đi qua cuộn cảm nó giống như chạy qua một dây dẫn kim loại (có điện trở nhỏ không đáng kể))
- Cường độ dòng điện trong mạch xoay chiều:
\(I = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Ta có:
${Z_L} = \omega L = \frac{{120\pi }}{{4\pi }} = 30\Omega $
Lúc đầu khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch, ta có:
$I = \frac{U}{R} = 1A \to R = \frac{U}{I} = 30\Omega $
Khi đặt vào hai đầu đoạn mạch điện áp u,
$\tan \varphi = \frac{{{Z_L}}}{R} = 1 \to \varphi = \frac{\pi }{4}$
=> Biểu thức cường độ dòng điện trong đoạn mạch là:
$i = 5c{\text{os(120}}\pi {\text{t - }}\frac{\pi }{4})A$
Đặt điện áp xoay chiều vào hai đầu đọa mạch có R, L, C mắc nối tiếp. Khi trong đoạn mạch có cộng hưởng điện thì điện áp giữa hai đầu đoạn mạch
-
A
lệch pha so với cường độ dòng điện trong mạch.
-
B
trễ pha so với dòng điện trong mạch.
-
C
cùng pha với cường độ dòng điện trong mạch.
-
D
sớm pha so với cường độ dòng điện trong mạch.
Đáp án của giáo viên lời giải hay : C
Hiện tượng cộng hưởng điện xảy ra khi \(Z_L=Z_C\)
Khi trong mạch xảy ra hiện tượng cộng hưởng điện thì: \(Z_L=Z_C\)
=> điện áp giữa hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch
Đặt điện áp \(u = 200\cos 100\pi t\left( V \right)\) vào hai đầu đoạn mạch gồm điện trở \(100 Ω\), cuộn cảm thuần và tụ điện mắc nối tiếp. Biết trong đoạn mạch có cộng hưởng điện. Cường độ hiệu dụng của dòng điện trong đoạn mạch là
-
A
\(2\sqrt 2 A\).
-
B
\(\sqrt 2 A\).
-
C
\(2A\).
-
D
\(1A\).
Đáp án của giáo viên lời giải hay : B
Trong mach xảy ra hiện tượng cộng hưởng điện thì \({Z_L} = {Z_C};Z = R\)
Khi mạch xảy ra hiện tượng cộng hưởng điện thì \({Z_L} = {Z_C};Z = R\), lúc này cường độ dòng điện hiệu dụng đạt giá trị cực đại \(I = \dfrac{U}{Z} = \dfrac{U}{R} = \dfrac{{100\sqrt 2 }}{{100}} = \sqrt 2 A\)
Đặt điện áp xoay chiều u = U0cos(ωt + φ) (V) (U0 và ω không đổi) vào hai đầu đoạn mạch gồm điện trở \(R\), tụ điện và cuộn cảm thuần mắc nối tiếp. Biết biểu thức cường độ dòng điện trong mạch là \({i_1} = \sqrt 5 {\rm{cos(}}\omega {\rm{t + }}\dfrac{\pi }{3})(A)\) . Nếu ngắt bỏ tụ điện \(C\) thì cường độ dòng điện trong mạch là \({i_2} = \sqrt 5 {\rm{cos(}}\omega {\rm{t - }}\dfrac{\pi }{6})(A)\). Nếu ngắt bỏ cuộn cảm thì cường độ dòng điện trong mạch là
-
A
\({i_3} = \sqrt 2 {\rm{cos(}}\omega {\rm{t - 1,107}})(A)\)
-
B
\({i_3} = \sqrt 2 {\rm{cos(}}\omega {\rm{t + 1,37}})(A)\)
-
C
\({i_3} = \dfrac{5}{{\sqrt 2 }}{\rm{cos(}}\omega {\rm{t - 1,107}})(A)\)
-
D
\({i_3} = \dfrac{5}{{\sqrt 2 }}{\rm{cos(}}\omega {\rm{t + 1,37}})(A)\)
Đáp án của giáo viên lời giải hay : B
Đoạn mạch RLC nối tiếp có uR cùng pha i, uL sớm pha π/2 so với i và uC chậm pha π/2 so với i
Tổng trở mạch RLC là \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)
Định luật Ôm cho đoạn mạch : I = U/Z
Sử dụng giản đồ vec tơ ghép:
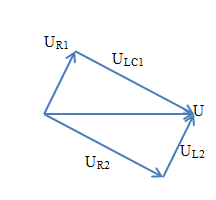
Vì I bằng nhau nên UR1 = UR2 vậy hình tạo thành là hình vuông
Ta có:
\(\left\{ \begin{array}{l}{Z_1} = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\{Z_2} = \sqrt {{R^2} + {Z_L}^2} \end{array} \right.\)
Vì đạt cùng điện áp hiệu dụng, mà giả thiết hai dòng điện có cùng giá trị hiệu dụng nên ta có:
\({Z_1} = {Z_2} \Leftrightarrow \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{R^2} + Z_L^2} \)
\( \Leftrightarrow {({Z_L} - {Z_C})^2} = Z_L^2 \Leftrightarrow \left| {{Z_L} - {Z_C}} \right| = {Z_L}\)
\( \Leftrightarrow {Z_C} = 2{{\rm{Z}}_L}\)
Theo bài ra, phương trình điện áp hai đầu đoạn mạch là:
\(u = {U_0}\cos \left( {\omega t + \varphi } \right)\left( V \right)\)
Độ lệch pha của dòng điện và điện áp trong mạch trong hai lần, lần lượt là:
\(\left\{ \begin{array}{l}\frac{{{Z_C} - {Z_L}}}{R} = \frac{\pi }{3} - \varphi \\\frac{{{Z_L}}}{R} = \varphi - \left( { - \frac{\pi }{6}} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\frac{{{Z_L}}}{R} = \frac{\pi }{3} - \varphi \\\frac{{{Z_L}}}{R} = \varphi + \frac{\pi }{6}\end{array} \right.\)
\( \Rightarrow \frac{\pi }{3} - \varphi = \varphi + \frac{\pi }{6} \Leftrightarrow \varphi = \frac{\pi }{{12}}\)
Mà UR1 = UL2 => \(R = {Z_L} = \left| {{Z_L} - {Z_C}} \right| \Rightarrow R = {Z_L} = \dfrac{1}{2}{Z_C}\)
Chuẩn hóa R = 1. Ta có :
\({I_{01}} = \dfrac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\sqrt {{1^2} + {{(2 - 1)}^2}} }} \Rightarrow I = \dfrac{U}{\sqrt 2} V\)
\({I_{03}} = \dfrac{U}{{{Z_C}}} = \dfrac{U}{2} = \sqrt 2 A\)
Mà i3 chỉ có tụ và điện trở nên pha ban đầu của i3 = 1,37 rad
Đặt điện áp xoay chiều \(u = 200cos\left( {100\pi t} \right)V\)vào hai đầu một đoạn mạch không phân nhánh. Đoạn mạch gồm điện trở thuần R, tụ điện có điện dung C, với \(R = {Z_C} = 100\Omega \). Cường độ dòng điện qua mạch là
-
A
\(i = \sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{4}} \right)A\)
-
B
\(i = 2\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{6}} \right)A\)
-
C
\(i = 2\sqrt 3 cos\left( {100\pi t - \dfrac{\pi }{6}} \right)A\)
-
D
\(i = 2\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{6}} \right)A\)
Đáp án của giáo viên lời giải hay : A
Cường độ dòng điện cực đại: \({I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{{U_0}}}{{\sqrt {{R^2} + Z_C^2} }}\)
Độ lệch pha giữa u và i: \(\tan \varphi = - \dfrac{{{Z_C}}}{R}\)
Độ lệch pha giữa u và i:
\(\begin{array}{l}\tan \varphi = - \dfrac{{{Z_C}}}{R} = - \dfrac{{100}}{{100}} = - 1 \Rightarrow {\varphi _u} - {\varphi _i} = - \dfrac{\pi }{4}\\ \Rightarrow {\varphi _i} = {\varphi _u} + \dfrac{\pi }{4} = \dfrac{\pi }{4}\end{array}\)
→ Phương trình của cường độ dòng điện: \(i = \sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{4}} \right)A\)
Đặt một điện áp \(u = 100\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{6}} \right)\left( V \right)\) (t tính bằng s) vào hai đầu đoạn mạch gồm cuộn cảm thuần có độ tự cảm \(\dfrac{1}{\pi }H\) và tụ điện có điện dung \(\dfrac{{{{2.10}^{ - 4}}}}{\pi }F\) mắc nối tiếp. Cường độ dòng điện qua đoạn mạch có phương trình là
-
A
\(i = 2cos\left( {100\pi t + \dfrac{\pi }{2}} \right)\left( A \right)\)
-
B
\(i = 2\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{3}} \right)\left( A \right)\)
-
C
\(i = 2\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{2}} \right)\left( A \right)\)
-
D
\(i = 2cos\left( {100\pi t - \dfrac{\pi }{2}} \right)\left( A \right)\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Sử dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức định luật ôm: \(I = \dfrac{U}{Z}\)
Ta có:
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \)
+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{2.10}^{ - 4}}}}{\pi }}} = 50\Omega \)
Tổng trở: \(Z = \left| {{Z_L} - {Z_C}} \right| = 50\Omega \)
Cường độ dòng điện cực đại trong mạch: \({I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{100\sqrt 2 }}{{50}} = 2\sqrt 2 A\)
Mạch chỉ có cuộn cảm thuần và tụ điện và có \({Z_L} > {Z_C} \Rightarrow \) điện áp nhanh pha \(\dfrac{\pi }{2}\) so với dòng điện
\( \Rightarrow {\varphi _i} = {\varphi _u} - \dfrac{\pi }{2} = \dfrac{\pi }{6} - \dfrac{\pi }{2} = - \dfrac{\pi }{3}\)
\( \Rightarrow \) Cường độ dòng điện qua đoạn mạch: \(i = 2\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{3}} \right)\)
Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm thuần có độ tự cảm \(\frac{1}{{4\pi }}H\), dòng điện trong đoạn mạch là dòng điện một chiều có cường độ 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp \(u = 150\sqrt 2 .\cos 120\pi t\left( V \right)\), biểu thức cường độ dòng điện trong đoạn mạch là:
-
A
\(i = 5.\cos \left( {120\pi t + \frac{\pi }{4}} \right)A\)
-
B
\(i = 5\sqrt 2 .\cos \left( {120\pi t - \frac{\pi }{4}} \right)A\)
-
C
\(i = 5\sqrt 2 .\cos \left( {120\pi t + \frac{\pi }{4}} \right)A\)
-
D
\(i = 5.\cos \left( {120\pi t - \frac{\pi }{4}} \right)A\)
Đáp án của giáo viên lời giải hay : D
Áp dụng định luật Ôm cho đoạn mạch có dòng điện một chiều chạy qua:
\(I = \frac{U}{R}\)
Áp dụng công thức tính điện trở đoạn mạch:
\(Z = \sqrt {{R^2} + {{\left( {\omega L} \right)}^2}} \)
Áp dụng định luật Ôm cho đoạn mạch xoay chiều:
\(I = \frac{U}{Z}\)
Tính góc lệch giữa pha của điện áp và dòng điện:
\(\tan \varphi = \frac{{\omega L}}{R}\)
Phương trình dòng điện :
\(i = I.\sqrt 2 .\cos \left( {\omega t + {\varphi _u} - \varphi } \right)V\)
Áp dụng định luật Ôm cho đoạn mạch có dòng điện một chiều chạy qua:
\(I = \frac{U}{R} \Rightarrow R = \frac{U}{I} = \frac{{30}}{1} = {30_{}}\Omega \)
Áp dụng công thức tính điện trở đoạn mạch:
\(Z = \sqrt {{R^2} + {{\left( {\omega L} \right)}^2}} = \sqrt {{{30}^2} + {{\left( {\frac{1}{{4\pi }}.120\pi } \right)}^2}} = 30{\sqrt 2 _{}}\Omega \)
Áp dụng định luật Ôm cho đoạn mạch xoay chiều:
\(I = \frac{U}{Z} = \frac{{150}}{{30\sqrt 2 }} = \frac{5}{{\sqrt 2 }}A\)
Tính góc lệch giữa pha của điện áp và dòng điện:
\(\tan \varphi = \frac{{\omega L}}{R} = \frac{{30}}{{30}} = 1 \Rightarrow \varphi = {\varphi _u} - {\varphi _i} = \frac{\pi }{4} \Rightarrow {\varphi _i} = - \frac{\pi }{4}\)
Phương trình dòng điện:
\(i = \frac{5}{{\sqrt 2 }}.\sqrt 2 .\cos \left( {120\pi t - \frac{\pi }{4}} \right)V = 5.\cos \left( {120\pi t - \frac{\pi }{4}} \right)A\)
Mắc lần lượt từng phần tử điện trở thuần R, cuộn dây thuần cảm L và tụ điện có điện dung C vào mạng điện xoay chiều có hiệu điện thế hiệu dụng UAB không đổi thì cường độ hiệu dụng của dòng điện tương ứng là 0,25A; 0,50A; 0,2A. Nếu mắc nối tiếp cả ba phần tử vào mạng điện xoay chiều nói trên thì cường độ hiệu dụng của dòng điện qua mạch là:
-
A
0,95A
-
B
0,20A
-
C
5,00A
-
D
0,39A
Đáp án của giáo viên lời giải hay : B
Áp dụng công thức định luật Ôm:
\(I = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{U_R}}}{R} = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Áp dụng công thức định luật Ôm cho đoạn mạch xoay chiều chỉ gồm một phần tử ta có:
\(\left\{ \begin{gathered}
{I_L} = \frac{U}{{{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{{I_L}}} \hfill \\
{I_C} = \frac{U}{{{Z_C}}} \Rightarrow {Z_C} = \frac{U}{{{I_C}}} \hfill \\
{I_R} = \frac{U}{R} \Rightarrow R = \frac{U}{{{I_R}}} \hfill \\
\end{gathered} \right.\)
Khi mắc cả 3 phần tử vào mạng điện xoay chiều nói trên:
\(\begin{gathered}
I = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{U}{{\sqrt {{{\left( {\frac{U}{{{I_R}}}} \right)}^2} + {{\left( {\frac{U}{{{I_L}}} - \frac{U}{{{I_C}}}} \right)}^2}} }} \hfill \\
\Rightarrow I\, = \frac{U}{{\sqrt {{{\left( {\frac{U}{{0,25}}} \right)}^2} + {{\left( {\frac{U}{{0,5}} - \frac{U}{{0,2}}} \right)}^2}} }} = 0,2A \hfill \\
\end{gathered} \)
Đoạn mạch AB gồm điện trở \(R = 40\Omega \), cuộn dây thuần cảm có độ tự cảm \(L =\frac{6}{{10\pi }}H\) và tụ điện C mắc nối tiếp. Đặt vào hai đầu đoạn mạch đó một điện áp xoay chiều \({u_{AB}} = 160co{\rm{s}}\left( {100\pi t + \frac{\pi }{6}} \right)\left( V \right)\) thì công suất tiêu thụ trên đoạn mạch đó bằng 320W. Biểu thức điện áp giữa hai đầu tụ điện là
-
A
\({u_C} = 240co{\rm{s}}\left( {100\pi t + \frac{\pi }{3}} \right)\left( V \right)\)
-
B
\({u_C} = 120\sqrt 2 co{\rm{s}}\left( {100\pi t - \frac{\pi }{3}} \right)\left( V \right)\)
-
C
\({u_C} = 120\sqrt 2 co{\rm{s}}\left( {100\pi t - \frac{\pi }{2}} \right)\left( V \right)\)
-
D
\({u_C} = 240co{\rm{s}}\left( {100\pi t - \frac{\pi }{3}} \right)\left( V \right)\)
Đáp án của giáo viên lời giải hay : D
+ Cảm kháng: \({Z_L} = \omega L\)
+ Công suất tiêu thụ của đoạn mạch: \(P = UIco{\rm{s}}\varphi = \frac{{{U^2}}}{{{Z^2}}}R\)
Ta có: \(\left\{ \begin{array}{l}R = 40\Omega \\{Z_L} = \omega L = 60\Omega \end{array} \right.\)
Công suất tiêu thụ trên đoạn mạch:
\(P = UIco{\rm{s}}\varphi = \frac{{{U^2}}}{{{Z^2}}}R \Leftrightarrow 320 = \frac{{{{\left( {80\sqrt 2 } \right)}^2}}}{{{Z^2}}}40\)
\( \Rightarrow Z = 40\Omega \Rightarrow {Z_L} = {Z_C} = 60\Omega \Rightarrow {\varphi _u} = {\varphi _i}\)
\( \Rightarrow {I_0} = \frac{{{U_0}}}{Z} = \frac{{160}}{{40}} = 4A \Rightarrow {U_{0C}} = {I_0}{Z_C} = 4.60 = 240V\)
Lại có: \({\varphi _{{u_C}}} - {\varphi _i} = - \frac{\pi }{2} \Rightarrow {\varphi _{{u_C}}} = {\varphi _i} - \frac{\pi }{2} = \frac{\pi }{6} - \frac{\pi }{2} = - \frac{\pi }{3}\)
\( \Rightarrow {u_C} = 240co{\rm{s}}\left( {100\pi t - \frac{\pi }{3}} \right)V\)
Đề thi THPT QG - 2020
Đặt điện áp \(u = 40\sqrt 2 cos\left( {100\pi t + \frac{\pi }{6}} \right)\left( V \right)\) vào hai đầu đoạn mạch gồm biến trở R và cuộn cảm thuần mắc nối tiếp. Điều chỉnh R đến giá trị để công suất tiêu thụ điện của đoạn mạch đạt cực đại. Khi đó, biểu thức điện áp giữa hai đầu điện trở là
-
A
\({u_R} = 40cos\left( {100\pi t - \frac{\pi }{{12}}} \right)\left( V \right)\)
-
B
\({u_R} = 40cos\left( {100\pi t + \frac{{5\pi }}{{12}}} \right)\left( V \right)\)
-
C
\({u_R} = 40\sqrt 2 cos\left( {100\pi t - \frac{\pi }{{12}}} \right)\left( V \right)\)
-
D
\({u_R} = 40\sqrt 2 cos\left( {100\pi t + \frac{{5\pi }}{{12}}} \right)\left( V \right)\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức suy ra từ bài toán R biến thiên để công suất cực đại: \(R = \left| {{Z_L} - {Z_C}} \right|\)
+ Sử dụng biểu thức: \(U_0^2 = U_{0R}^2 + {\left( {{U_{0L}} - {U_{0C}}} \right)^2}\)
+ Sử dụng biểu thức tính độ lệch pha của u so với i: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Viết phương trình điện áp
R thay đổi để công suất cực đại, khi đó ta có: \(R = {Z_L}\) \( \Rightarrow {U_{0R}} = {U_{0L}}\)
Lại có: \(U_0^2 = U_{0R}^2 + U_{0L}^2 \Rightarrow {U_{0L}} = {U_{0R}} = \frac{{{U_0}}}{{\sqrt 2 }} = 40V\)
Độ lệch pha của u so với i: \(\tan \varphi = \frac{{{Z_L}}}{R} = 1 \Rightarrow \varphi = \frac{\pi }{4}\)
Độ lệch pha của \({u_R}\) và \(u\) là: \(\Delta \varphi = \frac{\pi }{4} = {\varphi _{{u_u}}} - {\varphi _R}\)
\( \Rightarrow {\varphi _{{u_L}}} = {\varphi _u} - \frac{\pi }{4} = \frac{\pi }{6} - \frac{\pi }{4} = - \frac{\pi }{{12}}\)
\( \Rightarrow \) Biểu thức điện áp giữa hai đầu điện trở: \({u_R} = 40cos\left( {100\pi t - \frac{\pi }{{12}}} \right)V\)
Mạch điện xoay chiều gồm điện trở thuần \(R = 30\Omega \) mắc nối tiếp với cuộn dây. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều \(u = U\sqrt 2 .cos\left( {100\pi t} \right)V\) thì hiệu điện thế hiệu dụng ở hai đầu cuộn dây là \({U_d} = 60V\) và dòng điện trong mạch lệch pha \(\dfrac{\pi }{6}\) so với u và lệch pha \(\dfrac{\pi }{3}\) so với \({u_d}\). Hiệu điện thế hiệu dụng ở hai đầu mạch U có giá trị
-
A
120V
-
B
\(60\sqrt 3 V\)
-
C
90V
-
D
\(60\sqrt 2 V\)
Đáp án của giáo viên lời giải hay : B
Vẽ giản đồ vecto.
Sử dụng định lí hàm số cos: \({c^2} = {a^2} + {b^2} - 2.ab.cosC\)
Từ dữ kiện bài cho ta có giản đồ vecto:
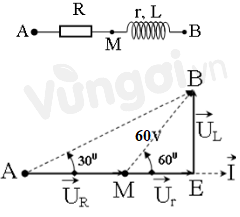
Từ hình vẽ ta có: \(\widehat {AMB} = {180^0} - \widehat {BME} = {120^0}\)
\( \Rightarrow \widehat {ABM} = {180^0} - \widehat {MAB} - \widehat {AMB} = {30^0}\)
\( \Rightarrow \Delta AMB\) cân tại M
\( \Rightarrow AM = MB = 60 \Leftrightarrow {U_R} = {U_d} = 60V\)
Áp dụng định lí hàm số cos trong tam giác AMB có:
\(\begin{array}{l}A{B^2} = A{M^2} + B{M^2} - 2.AM.BM.cos\widehat {AMB}\\ \Leftrightarrow {U^2} = U_R^2 + U_d^2 - 2.{U_R}{U_d}.cos\widehat {AMB}\\ \Leftrightarrow {U^2} = {60^2} + {60^2} - 2.60.60\cos 120 = 10800\\ \Rightarrow U = 60\sqrt 3 V\end{array}\)
