Một mạch điện xoay chiều có dạng như hình vẽ trong đó cuộn dây thuần cảm có cảm kháng \({Z_L} = 0,5R\), tụ điện có dung kháng \({Z_C} = 2R\). Khi khóa K đặt ở a, thì cường độ dòng điện qua cuộn dây có biểu thức \({i_1} = 0,4\sin \left( {100\pi t + \dfrac{\pi }{6}} \right)A\). Hỏi khi khóa K đặt tại b thì dòng điện qua C có biểu thức nào sau đây ?
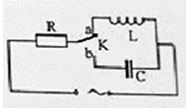
-
A
\(i = 0,1\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
B
\(i = 0,2\sin \left( {100\pi t + \dfrac{{2\pi }}{3}} \right)A\)
-
C
\(i = 0,1\sqrt 2 \sin \left( {100\pi t + \dfrac{\pi }{4}} \right)A\)
-
D
\(i = 0,2\sin \left( {100\pi t - \dfrac{\pi }{3}} \right)A\)
Đáp án của giáo viên lời giải hay : B
+ Áp dụng công thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng công thức tính độ lệch pha giữa u,i trong đoạn mạch xoay chiều R,L,C nối tiếp: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Khi K ở a thì mạch có R,L :
\( \to Z = \sqrt {{R^2} + Z_L^2} {\rm{}} = \dfrac{{\sqrt 5 R}}{2} = {\rm{}} > {U_0} = {I_0}.Z = 0,2\sqrt 5 R\)
+ Khi K ở b thì mạch có R,C:
\( \to Z' = \sqrt {{R^2} + Z_L^2} {\rm{}} = \sqrt 5 R = > {I_0} = \dfrac{{{U_0}}}{{Z'}} = 0,2A\)
+ Khi K ở a ta có:
\(\tan \varphi {\rm{}} = \dfrac{{{Z_L}}}{R} = 0,5 \to \varphi {\rm{}} = 26,565 \to {\varphi _u} = 30 + 26,565\)
+ Khi K ở b ta có:
\(\tan \varphi = - \dfrac{{{Z_C}}}{R} = - 2 \to \varphi {\rm{}} = 63,435 \to {\varphi _i} = 30 + 26,565 + 63,435 = 120 = \dfrac{{2\pi }}{3}\)
Vậy khi K ở b thì cường độ dòng điện qua C có biểu thức \(i = 0,2\sin \left( {100\pi t + \dfrac{{2\pi }}{3}} \right)A\)
Đặt điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos2}}\pi {\rm{ft}}\left( V \right)\) vào hai đầu đoạn mạch gồm điện trở \(R\), cuộn cảm thuần \(L\) và tụ điện \(C\) mắc nối tiếp nhau. Hệ số công suất của đoạn mạch khi đó là \(k\). Khi nối hai đầu cuộn cảm bằng một dây dẫn có điện trở không đáng kể thì điện áp hiệu dụng trên điện trở \(R\) tăng \(2\sqrt 2 \) lần và cường độ dòng điện qua đoạn mạch trong hai trường hợp lệch pha nhau một góc \(\dfrac{\pi }{2}\) . Giá trị của k bằng:
-
A
\(\dfrac{{\sqrt 3 }}{2}\)
-
B
\(\dfrac{2}{{\sqrt 5 }}\)
-
C
\(\dfrac{1}{3}\)
-
D
\(\dfrac{1}{2}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng giản đồ véc-tơ và biểu thức toán học
Ban đầu mạch gồm RLC mắc nối tiếp, ta gọi các giá trị điện áp trên các phần tử là \({U_R};{\rm{ }}{U_L};{\rm{ }}{U_{\bf{C}}}\)
Lúc sau, mạch được nối tắt qua L, nên chỉ còn R và C nối tiếp, ta gọi các điện áp trên các phần tử là \(U{'_L}\) và \(U{'_{\bf{C}}}\)
Biết rằng lúc sau dòng điện tức thời lệch pha \(\frac{\pi }{2}\) so với cường độ dòng điện lúc đầu, ta có: \(\left\{ \begin{array}{l}{\varphi _{i1}} = {\varphi _u} - {\varphi _1}\\{\varphi _{i2}} = {\varphi _u} - {\varphi _2}\end{array} \right. \Rightarrow {\varphi _{i1}} - {\varphi _{i2}} = \dfrac{\pi }{2} \Rightarrow {\varphi _2} - {\varphi _1} = \dfrac{\pi }{2}\)
Ta vẽ trên cùng 1 giản đồ véc-tơ:
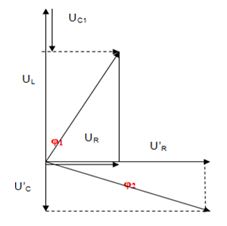
Ta có: \({\varphi _1} + \left| {{\varphi _2}} \right| = \dfrac{{\pi {\rm{}}}}{2};\cos {\varphi _1} = \dfrac{{{U_R}}}{{{U_{AB}}}} = k;\cos {\varphi _2} = {\rm{ }}\dfrac{{{U_R}}}{{{U_{AB}}}} = \dfrac{{2.\sqrt 2 .{U_R}}}{{{U_{AB}}}} = 2\sqrt 2 .k\)
Mặt khác :
\({\varphi _1} + \left| {{\varphi _2}} \right| = \dfrac{{\pi {\rm{}}}}{2} \Rightarrow \cos {\varphi _1} = \sin {\varphi _2} \Leftrightarrow k = \sqrt {1 - {{(\cos {\varphi _2})}^2}} {\rm{}} = \sqrt {1 - 8{k^2}} {\rm{}} \Leftrightarrow {k^2} = 1 - 8{k^2} \Leftrightarrow 9{k^2} = 1 \Leftrightarrow k = \dfrac{1}{3}\)
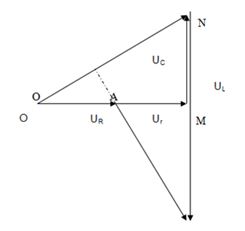
Đặt điện áp xoay chiều vào mạch điện \(AB\) gồm ba đoạn mạch nối tiếp: \(AM\) có cuộn dây thuần cảm với hệ số tự cảm \({L_1}\) ; \(MN\) có cuộn dây có hệ số tự cảm \({L_2}\); \(NB\) có tụ điện với điện dung \(C\). Biết điện áp tức thời trên \(MN\) trễ pha \(\dfrac{\pi }{6}\) so với điện áp trên \(AB\), \({U_{MN}} = {\text{ }}2{U_C}\) , \({Z_{L1}} = {\text{ }}5{Z_C}\). Hệ số công suất của đoạn mạch \(MN\) gần với giá trị nào sau đây nhất?
-
A
\(\dfrac{1}{2}\)
-
B
\(\dfrac{1}{{\sqrt 2 }}\)
-
C
\(\dfrac{1}{{\sqrt 3 }}\)
-
D
\(\dfrac{{\sqrt 3 }}{2}\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng giản đồ véc-tơ
+ Sử dụng các hệ thức lượng trong tam giác
Vì điện áp tức thời trên \(MN\) trễ pha so với \({U_{AB}}\) , tức là cuộn dây có điện trở \(r\).
Nhiệm vụ của bài là đi tìm hệ số công suất của đoạn mạch \(MN\), hay là tìm \(cos{\varphi _{MN}}\).
Từ đề bài ta vẽ được giản đồ vecto như sau :
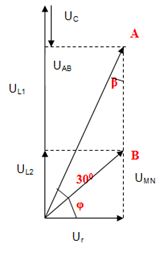
Xét tam giác \(OAB\);
Sử dụng định lí hàm số sin trong tam giác ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin \left( {{{30}^0}} \right)}} = \dfrac{{OB}}{{\sin \beta }} \Leftrightarrow \dfrac{{4{U_C}}}{{0,5}} = \dfrac{{2{U_C}}}{{\sin \beta }}\\ \Rightarrow \sin \beta = \dfrac{1}{4} \Rightarrow \beta = {14^0}28'\\ \Rightarrow \varphi = {90^0} - \beta - {30^0} = {45^0}31'\\ \Rightarrow \cos \varphi \approx \dfrac{1}{{\sqrt 2 }}\end{array}\)
Đặt điện áp xoay chiều \(u = {U_0}{\rm{cos}}\left( {\dfrac{{2\pi }}{T}t + \varphi } \right)V\) vào hai đầu đoạn mạch \(AB\) như hình bên. Biết \(R{\rm{ }} = {\rm{ }}r\). Đồ thị biểu diễn điện áp \({u_{AN}}\) và \({u_{MB}}\) như hình vẽ bên cạnh. Giá trị của U0 bằng:
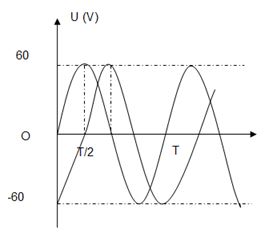
-
A
\(84,85{\rm{ }}V\)
-
B
\(75,89V\)
-
C
\(107,33V\)
-
D
\(120V\)
Đáp án của giáo viên lời giải hay : B
Vẽ giản đồ vec tơ của mạch điện, sử dụng các tính chất hình học
Từ đồ thị ta thấy được các giá trị
Tại thời điểm ban đầu \(t{\rm{ }} = {\rm{ }}0\), thì điện áp trên đoạn \(AN\) bằng \(0\), điện áp trên đoạn \(MB\) đạt cực tiểu (ở biên âm), dao động với cùng chu kì, nên ta thấy được điện áp trên đoạn mạch \(MB\) trễ pha so với điện áp trên đoạn mạch \(AN\) một góc là \(\dfrac{\pi }{2}\). Hay điện áp tức thời trên hai đoạn mạch này vuông pha với nhau. Mặt khác \(R{\rm{ }} = {\rm{ }}r\) nên ta có
Ta vẽ được giản đồ vecto như sau:
Tam giác \(OMN\) bằng với tam giác \(BMA\) theo trường hợp cạnh huyền và góc vuông (\(ON{\rm{ }} = {\rm{ }}AB\); \(\widehat O = \widehat B\))
Từ đó suy ra được :
\( \to {U_{R0}} = {U_{r0}} = \dfrac{{60}}{{\sqrt 5 }}V\)
\(U_0^2 = {\left( {2{U_{r0}}} \right)^2} + {(2{U_{r0}})^2} = \dfrac{{{{8.60}^2}}}{5} \Rightarrow {U_0} = \dfrac{{120\sqrt 2 }}{{\sqrt 5 }} = 75,89V\)
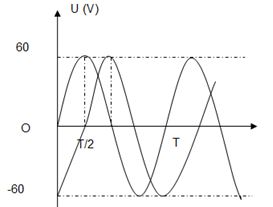
Mạch điện \(AB\) gồm đoạn \(AM\) và đoạn \(MB\): Đoạn \(AM\) có một điện trở thuần \(50\Omega \) và đoạn \(MB\) có một cuộn dây. Đặt vào mạch \(AB\) một điện áp xoay chiều thì điện áp tức thời của hai đoạn \(AM\) và \(MB\) biến thiên như trên đồ thị:
Cảm kháng của cuộn dây là:
-
A
\(12,5\sqrt 2 \Omega \)
-
B
\(12,5\sqrt 3 \Omega \)
-
C
\(12,5\sqrt 6 \Omega \)
-
D
\(25\sqrt 6 \Omega \)
Đáp án của giáo viên lời giải hay : C
+ Kĩ năng đọc đồ thị
+ Sử dụng biểu thức định luật Ôm: \(I = \dfrac{U}{Z}\)
Ta có:
Đoạn \(MB\) là cuộn dây, đoạn \(AM\) chỉ có điện trở nên \({u_{MB}}\) sớm pha hơn \({u_{AM}}\)
Một chu kỳ ứng với \(12\) khoảng, nên ta thấy \({u_{MB}}\) sớm pha hơn \({u_{AM}}\) một góc \(\dfrac{{\pi {\rm{}}}}{3}\) ; \({u_{AM}}\) cùng pha với cường độ dòng điện nên \({u_{MB}}\) sớm pha hơn cường độ dòng điện một góc \(\dfrac{{\pi {\rm{}}}}{3}\)
\(I = \dfrac{{{U_R}}}{R} = \dfrac{{100\sqrt 2 }}{{\sqrt {2.} 50}} = 2(A)\)
=> \({Z_{MB}} = \dfrac{{{U_{MB}}}}{I} = \dfrac{{100}}{{\sqrt 2 .2}} = 25\sqrt 2 \Omega \)
Giải hệ \(\left\{ \begin{array}{l}{2.25^2} = {r^2} + Z_L^2\\\dfrac{{{Z_L}}}{r} = \sqrt 3 \end{array} \right.\)
=>\({Z_L} = 12,5\sqrt 6 \Omega \)
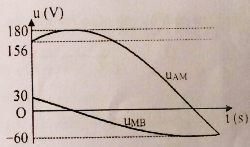
Đặt điện áp xoay chiều vào hai đầu đoạn mạch \(AB\) gồm: đoạn mạch \(AM\)chứa điện trở thuần \(R = 90\Omega \) và tụ điện \(C = 35,4\mu F\), đoạn mạch \(MB\) gồm hộp \(X\) chứa \(2\) trong \(3\) phần tử mắc nối tiếp (điện trở thuần \({R_0}\); cuộn cảm thuần có độ tự cảm \({L_0}\); tụ điện có điện dung \({C_0}\)). Khi đặt vào hai đầu \(AB\) một điện thế xoay chiều có tần số \(50Hz\) thì ta được đồ thị sự phụ thuộc của \({u_{AM}}\) và \({u_{MB}}\) theo thời gian như hình vẽ (chú ý \(90\sqrt 3 {\rm{}} \approx 156\) ). Giá trị của các phần tử trong hộp \(X\) là:
-
A
\({R_0} = {\rm{ }}60\Omega ;{L_0} = {\rm{ }}165mH\)
-
B
\({R_0} = {\rm{ }}30\Omega ;{L_0} = {\rm{ }}95,5mH\)
-
C
\({R_0} = {\rm{ }}60\Omega ;{L_0} = {\rm{ }}61,3mH\)
-
D
\({R_0} = {\rm{ }}30\Omega ;{L_0} = {\rm{ }}106mH\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng các công thức của dòng điện xoay chiều kết hợp kĩ năng đọc đồ thị
+ \({\varphi _1} + {\varphi _2} = \dfrac{\pi }{2} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\)
Ta có: \(R = 90W,{Z_C} = 90W\)
Từ đồ thị, ta có: \({U_{{0_{AM}}}} = 180V;{U_{{0_{MB}}}} = 60V\)
Tại thời điểm \(t{\rm{ }} = {\rm{ }}0\), ta có: \({u_{AM}} = 156\)
và đang tăng $ \to {u_{AM}} = 156 = 180c{\rm{os}}{\varphi _1} \to {\varphi _1} = {\rm{}} - {30^0}$ \({u_{MB}} = {\rm{ }}30\)
và đang giảm \( \to {u_{AM}} = 30 = 60c{\rm{os}}{\varphi _2} \to {\varphi _2} = {60^0}\)
\( \to {\varphi _2} - {\varphi _1} = {90^0} \to {u_{AM}} \bot {u_{MB}}\)
=> hộp \(X\) gồm \(2\) phần tử \({R_0}\) và \({L_0}\)
\({u_{AM}} \bot {u_{MB}} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1 \leftrightarrow \dfrac{{{Z_{{L_0}}}}}{{{R_0}}}\dfrac{{{Z_C}}}{R} = 1 \leftrightarrow \dfrac{{{Z_{{L_0}}}}}{{{R_0}}}\dfrac{{90}}{{90}} = 1 \to {Z_{{L_0}}} = {R_0}\)
Mặt khác, ta có:
\(\begin{array}{l}\dfrac{{{U_{{0_{AM}}}}}}{{{U_{{0_{MB}}}}}} = \dfrac{{{Z_{AM}}}}{{{Z_{MB}}}} = \dfrac{{180}}{{60}} = 3 \to {Z_{AM}} = 3{Z_{MB}}\\ \leftrightarrow \sqrt {R_0^2 + Z_{{L_0}}^2} = 3.\sqrt {{{90}^2} + {{90}^2}} \to {R_0} = {Z_{{L_0}}} = 30\Omega \to \left\{ \begin{array}{l}{R_0} = 30\Omega \\{L_0} = 95,9mH\end{array} \right.\end{array}\)
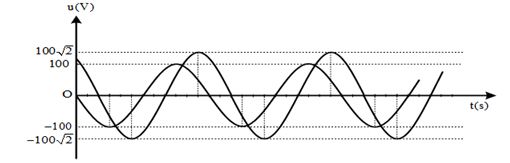
Trên đoạn mạch không phân nhánh có bốn điểm theo đúng thứ tự \(A,{\rm{ }}M,{\rm{ }}N,{\rm{ }}B\). Giữa \(A\) và \(M\) chỉ có điện trở thuần. Giữa \(M\) và \(N\) chỉ có cuộn dây. Giữa \(N\) và \(B\) chỉ có tụ điện. Đặt vào hai đầu đoạn mạch \(AB\) một điện áp xoay chiều có hiệu điện thế hiệu dụng \(U\). Khi đó công suất tiêu thụ trên đoạn mạch \(AM\) bằng công suất tiêu thụ trên đoạn mạch \(MN\). Sự phụ thuộc của hiệu điện thế tức thời hai đầu \(AN\) và \(MB\) theo thời gian được cho như trên đồ thị. Giá trị của \(U\) xấp xỉ bằng:

-
A
24,1 V
-
B
26,8 V
-
C
21,6 V
-
D
28,8 V
Đáp án của giáo viên lời giải hay : D
Sử dụng giản đồ véc–tơ
Dựa vào đồ thị và dữ kiện đề bài: \(\left\{ \begin{array}{l}R = r \Rightarrow {U_R} = {U_r}\\\overrightarrow {{U_{AN}}} \bot \overrightarrow {{U_{MB}}} \end{array} \right.\)
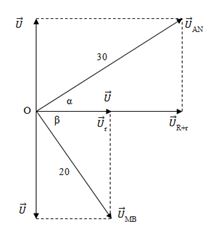
Ta có: \(\alpha {\rm{}} + \beta {\rm{}} = \dfrac{{\pi {\rm{}}}}{2} \Rightarrow c{\rm{os}}\beta {\rm{}} = \sin \alpha {\rm{}} \Rightarrow \dfrac{{{U_R}}}{{20}} = \dfrac{{{U_L}}}{{30}} \Rightarrow {U_L} = \dfrac{{{U_R}.30}}{{20}} = 1,5{U_R} \Rightarrow {Z_L} = 1,5R\)
\(\begin{array}{l}\dfrac{{U_{MB}^2}}{{U_{AN}^2}} = \dfrac{{Z_{MB}^2}}{{Z_{AN}^2}} = \dfrac{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{{\left( {2R} \right)}^2} + Z_L^2}} = \dfrac{{{{20}^2}}}{{{{30}^2}}} = \dfrac{4}{9} \Leftrightarrow \dfrac{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{{\left( {2R} \right)}^2} + {{\left( {1,5R} \right)}^2}}} = \dfrac{4}{9} \Rightarrow {\left( {{Z_L} - {Z_C}} \right)^2} = \dfrac{{16}}{9}{R^2}\\\dfrac{{{U^2}}}{{U_{AN}^2}} = \dfrac{{Z_{MB}^2}}{{Z_{AN}^2}} = \dfrac{{{{\left( {2R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} \Leftrightarrow \dfrac{{{U^2}}}{{{{20}^2}}} = \dfrac{{4{R^2} + \dfrac{{16}}{9}{R^2}}}{{{R^2} + \dfrac{{16}}{9}{R^2}}} \Rightarrow U = 28,8V\end{array}\)
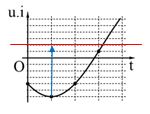
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì dòng điện trong đoạn mạch có cường độ i. Hình bên là một phần đồ thị biểu diễn sự phụ thuộc của tích u.i theo thời gian t. Hệ số công suất của đoạn mạch là:
-
A
\(0,71\)
-
B
\(0,50\)
-
C
\(0,25\)
-
D
\(0,20\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính công suất: \(p = ui\)
+ Sử dụng vòng tròn lượng giác
\(p = ui = {U_o}{I_o}c{\rm{os}}\omega {\rm{t}}{\rm{.cos}}\left( {\omega {\rm{t + }}\varphi } \right) = UI.c{\rm{os}}\left( {{\rm{2}}\omega {\rm{t + }}\varphi } \right) + UIc{\rm{os}}\varphi \)
\(p\) biến thiên điều hòa quanh \({p_o} = UIc{\rm{os}}\varphi \) với biên độ \(U.I\)
Dùng vòng tròn lượng giác ta có:
\(\left\{ \begin{array}{l}c{\rm{os}}\alpha {\rm{ = }}\frac{{{\rm{UI - 2}}}}{{{\rm{UI}}}}\\c{\rm{os2}}\alpha {\rm{ = }}\frac{{{\rm{UI - 7}}}}{{{\rm{UI}}}}\\c{\rm{os2}}\alpha {\rm{ = 2co}}{{\rm{s}}^{\rm{2}}}\alpha - 1\end{array} \right. \to UI = 8\)
\(UIc{\rm{os}}\varphi {\rm{ = }}\left( {{\rm{8 - 6}}} \right) \to c{\rm{os}}\varphi = \frac{2}{8} = 0,25\)
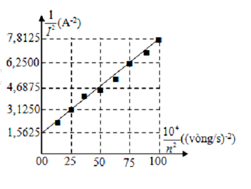
Nối hai cực của máy phát điện xoay chiều một pha vào hai đầu một cuộn dây không thuần cảm có điện trở \(r = 10\pi {\rm{ }}\Omega \) và độ tự cảm L. Biết rôto của máy phát có một cặp cực, stato của máy phát có \(20\) vòng dây và điện trở thuần của cuộn dây là không đáng kể. Cường độ dòng điện trong mạch được đo bằng đồng hồ đo điện đa năng hiện số. Kết quả thực nghiệm thu được như đồ thị trên hình vẽ. Giá trị của L là:
-
A
\(0,25{\rm{ }}H\)
-
B
\(0,30{\rm{ }}H\)
-
C
\(0,20{\rm{ }}H\)
-
D
\(0,35{\rm{ }}H\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính suất điện động hiệu dụng \(E = \omega {\phi _0}\)
+ Cường độ dòng điện hiệu dụng \(I = \frac{E}{Z}\)
+ Tần số của dòng điện xoay chiều \(f{\rm{ }} = {\rm{ }}np\) (n là tốc độ quay của roto ; p là số cặp cực)
Ta có : \(I = \frac{{\omega \Phi }}{{\sqrt {{r^2} + {\omega ^2}{L^2}} }} \Rightarrow \frac{1}{{{I^2}}} = \frac{{{r^2}}}{{{\omega ^2}{\Phi ^2}}} + \frac{{{L^2}}}{{{\Phi ^2}}}\)
Có : \(f = np;p = 1 = > \omega = 2\pi n;r = 10\pi \left( \Omega \right)\)
\({\rm{}} \Rightarrow \frac{1}{{{I^2}}} = \frac{{{r^2}}}{{4{\pi ^2}{n^2}{\Phi ^2}}} + \frac{{{L^2}}}{{{\Phi ^2}}} + \frac{{{{10}^4}}}{{{n^2}}} = 0 \Rightarrow \frac{1}{{{n^2}}} = 0 \Rightarrow \frac{1}{{I_0^2}} = \frac{{{L^4}}}{{{\Phi ^2}}} = 1,5625\)
+ Lại có: \(\frac{{{{10}^4}}}{{{n^2}}} = 100 \Rightarrow \frac{1}{{{n^2}}} = 0,01 \Rightarrow \frac{1}{{{I^2}}} = \frac{{{r^2}}}{{100.4{\pi ^2}{\Phi ^2}}} + \frac{{{L^2}}}{{{\Phi ^2}}} = 7,8125\) (2)
+Lấy \(\frac{{(1)}}{{(2)}} = \frac{{{L^2}}}{{\frac{{{r^2}}}{{100.4{\pi ^2}}} + {L^2}}} = \frac{{1,5625}}{{7,8125}} = \frac{1}{5} \Rightarrow L = 0,25H\)
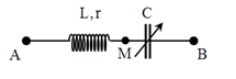
Cho mạch điện như hình vẽ. Đặt vào hai đầu \(A,{\rm{ }}B\) một điện áp xoay chiều có giá trị hiệu dụng \(U\) và tần số \(f\) không đổi. Điều chỉnh \(C\) để tổng điện áp hiệu dụng \({U_{AM}} + {\text{ }}{U_{MB}}\) lớn nhất thì tổng đó bằng \(2U\) và khi đó công suất tiêu thụ của đoạn mạch \(AM\) là \(36{\rm{ }}W\). Tiếp tục điều chỉnh \(C\) để công suất tiêu thụ của đoạn mạch lớn nhất thì công suất lớn nhất đó bằng:
-
A
\(32{\rm{ }}W\)
-
B
\(36{\rm{ }}W\)
-
C
\(25{\rm{ }}W\)
-
D
\(48{\rm{ }}W\)
Đáp án của giáo viên lời giải hay : D
Áp dụng phương pháp giản đồ vectơ trong mạch điện xoay chiều
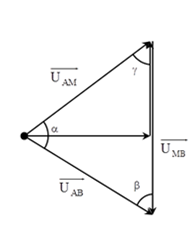
+ Áp dụng định lý sin trong tam giác, ta có: \(\dfrac{{{U_{AM}}}}{{\sin \beta }} = \dfrac{{{U_{MB}}}}{{\sin \alpha }} = \dfrac{{{U_{AB}}}}{{\sin \gamma }} \to {U_{AM}} + {U_{MB}} = \dfrac{{{U_{MB}}}}{{\sin \gamma }}\left( {\sin \alpha {\rm{}} + \sin \beta } \right)\)
với \(\gamma \) luôn không đổi.
Biến đổi lượng giác \({U_{AM}} + {U_{MB}} = \dfrac{{2{U_{AB}}}}{{\sin \gamma }}\sin \left( {\dfrac{{180 - \gamma }}{2}} \right)\cos \left( {\dfrac{{\alpha {\rm{}} - \beta }}{2}} \right)\)
+ Khi đó: \({\left( {{U_{AM}} + {U_{MB}}} \right)_{\max }} = \dfrac{{2U}}{{\sin \gamma }}\sin \left( {\dfrac{{180 - \gamma }}{2}} \right) = 2U \to \gamma {\text{}} = {60^\circ }.\)
Các vecto hợp với nhau thành tam giác đều => khi xảy ra cực đại u chậm pha hơn i một góc \({30^0}\).
\(P = {P_{\max }}{\cos ^2}\varphi {\text{}} \to {P_{\max }} = \dfrac{P}{{{{\cos }^2}\varphi }} = \dfrac{{36}}{{{{\cos }^2}{{30}^\circ }}} = 48{\mkern 1mu} {\mkern 1mu} W.\)
Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần \(R = 100\sqrt 2 \Omega \) , cuộn cảm thuần \(L = \dfrac{5}{{3\pi }}H\) và tụ điện \(C = \dfrac{{{{5.10}^{ - 4}}}}{{6\pi }}F\) mắc nối tiếp. Bỏ qua điện trở các cuộn dây của máy phát điện và điện trở dây nối. Máy phát điện có số cặp cực không đổi, tốc độ quay của roto thay đổi được. Khi tốc độ quay của roto bằng \(n\) (vòng/phút) thì công suất của mạch đạt giá trị lớn nhất bằng $161,5W$. Khi tốc độ quay của roto bằng \(2n\) (vòng/phút) thì công suất tiêu thụ của mạch là:
-
A
\(136W\)
-
B
\(126W\)
-
C
\(148W\)
-
D
\(125W\)
Đáp án của giáo viên lời giải hay : A
Công thức tính công suất tiêu thụ của mạch: \(P = \dfrac{{{U^2}R}}{{{Z^2}}} = \dfrac{{{{\left( {\dfrac{{\omega {\Phi _0}}}{{\sqrt 2 }}} \right)}^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{{\omega ^2}{\Phi ^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)

+ Khi tốc độ quay của roto là \(n\) (vòng/phút): \(\begin{array}{l}P = \frac{{{\omega ^2}{\Phi ^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \frac{{{\omega ^2}{\Phi ^2}.R}}{{{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}}} = \frac{{{\omega ^2}{\Phi ^2}.R}}{{{R^2} + {\omega ^2}{L^2} - \frac{{2L}}{C} + \frac{1}{{{\omega ^2}{C^2}}}}}\\ = \frac{{{\Phi ^2}.R}}{{\frac{{{R^2}}}{{{\omega ^2}}} + {L^2} - \frac{{2L}}{{{\omega ^2}C}} + \frac{1}{{{\omega ^4}{C^2}}}}} \Rightarrow P = \frac{{{\Phi ^2}.R}}{{\frac{1}{{{\omega ^4}{C^2}}} + \left( {{R^2} - \frac{{2L}}{C}} \right)\frac{1}{{{\omega ^2}}} + {L^2}}}\\{P_{\max }} \Leftrightarrow {\left( {\frac{1}{{{\omega ^4}{C^2}}} + \left( {{R^2} - \frac{{2L}}{C}} \right)\frac{1}{{{\omega ^2}}} + {L^2}} \right)_{\min }}\\ \Leftrightarrow \frac{1}{{{\omega ^2}}} = \frac{{\frac{{2L}}{C} - {R^2}}}{{\frac{2}{{{C^2}}}}} = \frac{{2\frac{5}{{3\pi }}.\frac{{6\pi }}{{{{5.10}^{ - 4}}}} - {{\left( {100\sqrt 2 } \right)}^2}}}{{\frac{2}{{{{\left( {\frac{{6\pi }}{{{{5.10}^{ - 4}}}}} \right)}^2}}}}} = \frac{1}{{14400{\pi ^2}}}\\ \Rightarrow \omega = 120\pi \Rightarrow \left\{ \begin{array}{l}{Z_L} = \omega L = 120\pi .\frac{5}{{3\pi }} = 200\Omega \\{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{120\pi .\frac{{{{5.10}^{ - 4}}}}{{6\pi }}}} = 100\Omega \end{array} \right.\\ \Rightarrow {P_{m{\rm{ax}}}} = \frac{{{\omega ^2}{\Phi ^2}R}}{{{R^2} + {{\left( {200 - 100} \right)}^2}}} = 161,5(*)\end{array}\)
+ Khi tốc độ quay của roto là \(2n\) (vòng/phút) \( \Rightarrow \left\{ \begin{array}{l}{Z_L}^\prime = 2{Z_L} = 400\Omega \\{Z_C}^\prime = \frac{{{Z_C}}}{2} = 50\Omega \end{array} \right. \Rightarrow P' = \frac{{\omega {'^2}{\Phi ^2}R}}{{{R^2}}} + {\left( {{Z_L}^\prime - {Z_C}^\prime } \right)^2} = \frac{{4{\omega ^2}R}}{{{R^2} + {{\left( {400 - 50} \right)}^2}}}(**)\)
Từ (*) và (**)
\({\rm{}} \Rightarrow \frac{{P'}}{{{P_{m{\rm{ax}}}}}} = {\rm{ }}\frac{{\omega {'^2}}}{{{\omega ^2}}}.\frac{{{R^2} + {{\left( {200 - 100} \right)}^2}}}{{{R^2} + {{\left( {400 - 50} \right)}^2}}} \Leftrightarrow \frac{{P'}}{{161,5}} = 4.\frac{{{{\left( {100\sqrt 2 } \right)}^2} + {{100}^2}}}{{{{\left( {100\sqrt 2 } \right)}^2} + {{350}^2}}} = \frac{{16}}{{19}} \Rightarrow P' = 136W\)
Một quạt điện mà dây quấn có điện trở thuần \(16\Omega \), được mắc vào nguồn điện xoay chiều \({u_1} = 110\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)V\) thì chạy bình thường và sản ra công cơ học \(40W\), trong điều kiện đó hệ số công suất của động cơ là \(0,8\). Mắc nối tiếp quạt với tụ điện và mắc vào nguồn điện mới \({u_2} = 220\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)V\) thì quạt vẫn chạy bình thường. Điện dung của tụ điện gần giá trị nào nhất sau đây?
-
A
\(7{\rm{ }}\mu F\)
-
B
\(6{\rm{ }}\mu F\)
-
C
\(5{\rm{ }}\mu F\)
-
D
\(8{\rm{ }}\mu F\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính công suất tiêu thụ: \(P{\rm{ }} = {\rm{ }}UIcos\varphi \)
+ Sử dụng công thức tính công cơ học: \({P_{ch}} = {\rm{ }}P{\rm{ }} - {\rm{ }}{P_{hp}}\)
+ Quạt được mắc vào nguồn điện \({u_1} = 110\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)V\)
Công cơ học:
\(\begin{array}{l}{P_{ch}} = P - {P_{hp}} \Leftrightarrow 40 = UI\cos \varphi - {I^2}R \Leftrightarrow 40 = 110.I.0,8 - 16{I^2}\\ \Leftrightarrow 16{I^2} - 88I + 40 = 0\\ \Rightarrow \left[ \begin{array}{l}I = 5A\\I = 0,5A\end{array} \right.\end{array}\)
- TH1: \(I = 5A \Rightarrow {Z_1} = \sqrt {{{16}^2} + Z_{L1}^2} {\rm{}} = 22 \Rightarrow {Z_{L1}} = 15,1\Omega \)
- TH2: \(I = 0,5A \Rightarrow {Z_2} = \sqrt {{{16}^2} + Z_{L2}^2} {\rm{}} = 220 \Rightarrow {Z_{L2}} = 219,4\Omega \)
+ Mắc nối tiếp quạt với tụ điện và mắc vào nguồn điện \({u_2} = 220\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)V\) thì quạt vẫn sáng bình thường => \(I' = I\)
- TH1: \(I' = I = 5A \Rightarrow Z' = \sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}} {\rm{}} = \dfrac{{220}}{5} = 44\)
\( \Leftrightarrow {16^2} + {\left( {15,1 - {Z_{C1}}} \right)^2} = {44^2} \Rightarrow {Z_{C1}} = 56,1 \Rightarrow C = 56,7\mu F\)
- TH2:
\(\begin{array}{l}I' = I = 0,5A \Rightarrow Z' = \sqrt {{R^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}} = \dfrac{{220}}{{0,5}} = 440\\ \Leftrightarrow {16^2} + {\left( {219,4 - {Z_{C2}}} \right)^2} = {440^2} \Rightarrow {Z_{C2}} = 659,1 \Rightarrow C = 4,83\mu F\end{array}\)
Cho đoạn mạch \(AB\) gồm cuộn dây thuần có điện trở thuần \(100\Omega \) và độ tự cảm \(\dfrac{1}{\pi }H\) mắc nối tiếp với tụ điện có điện dung \(\dfrac{{{{10}^{ - 4}}}}{{2\pi }}F\) . Đặt vào hai đầu đoạn mạch \(AB\) một điện áp xoay chiều \({u_{AB}} = 200\cos 100\pi t(V)\) . Khi điện áp tức thời giữa hai đầu đoạn mạch \(AB\) là \(100\sqrt 3 V\) và đang giảm thì điện áp tức thới giữa hai đầu cuộn dây là:
-
A
\( - 100{\rm{ }}V\) và đang giảm
-
B
\(-{\rm{ }}100{\rm{ }}V\) và đang tăng
-
C
\(100{\rm{ }}V\) và đang giảm
-
D
\(100{\rm{ }}V\) và đang tăng
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính độ lệch pha giữa điện áp và cường độ dòng điện: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Sử dụng biểu thức định luật Ôm, viết phương trình điện áp
Tổng trở của mạch là \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = \sqrt {{{100}^2} + \left( {100\pi .\frac{1}{\pi } - \frac{1}{{\frac{{{{10}^{ - 4}}.100\pi }}{{2\pi }}}}} \right)} {\rm{}} = 100\sqrt 2 \Omega {\rm{}}\)
Độ lệch pha giữa u và i được xác định bởi biểu thức: \(\tan \varphi {\rm{}} = \frac{{{Z_l} - {Z_C}}}{R} = \frac{{100 - 200}}{{100}} = {\rm{}} - 1 = {\rm{}} > \varphi {\rm{}} = {\rm{}} - \frac{\pi }{4}\)
Biểu thức cường độ dòng điện \(i = \sqrt 2 \cos \left( {100\pi t - \frac{\pi }{4}} \right)A\)
Độ lệch pha giữa ud và i được xác định bởi biểu thức: \(\tan {\varphi _d} = \frac{{{Z_L}}}{R} = \frac{{100}}{{100}} = 1 = {\rm{}} > {\varphi _d} = \frac{\pi }{4}\)
Biểu thức điện áp hai đầu cuộn dây là \({u_d} = \sqrt {{R^2} + Z_L^2} .{I_0}\cos \left( {100\pi t + \frac{\pi }{2}} \right) = 200\cos (100\pi t + \frac{\pi }{2})\)
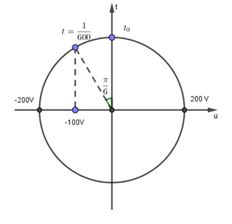
Tại thời điểm t: \({u_{AB}} = 100\sqrt 3 = 200\cos 100\pi t = > t = \frac{1}{{600}}s{\rm{}}\)
\( = > {u_d} = 200\cos \left( {100\pi t + \frac{\pi }{2}} \right) = 200\cos \left( {100\pi \frac{1}{{600}} + \frac{\pi }{2}} \right) = - 100V\)
Ta có \(t = \frac{1}{{600}}s \Leftrightarrow \frac{T}{{12}} \Leftrightarrow \frac{\pi }{6}\) biểu diễn trên đường tròn lượng giác ta thấy điện áp ở hai đầu cuộn dây đang giảm:
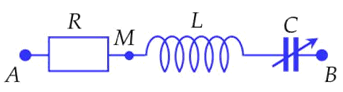
Cho mạch điện như hình vẽ bên. Cuộn dây thuần cảm. Tụ điện có điện dung C biến đổi. Đặt vào hai đầu đoạn mạch một điện áp \(u = U\sqrt 2 .\cos \left( {\omega t + \varphi } \right)\) (trong đó U, ɷ, φ không đổi). Khi C = C1biểu thức của điện áp hai đầu R là \({u_{AM}} = 126.\cos \left( {\omega t - \frac{\pi }{4}} \right)V\). Khi C = C2biểu thức của điện áp hai đầu R là \({u_{AM}} = 77.\cos \left( {\omega t + \frac{\pi }{3}} \right)V\). Điện áp U gần nhất với giá trị nào sau đây?
-
A
115V.
-
B
127V.
-
C
107V.
-
D
108V.
Đáp án của giáo viên lời giải hay : A
Áp dụng giản đồ vecto và sử dụng góc lệch pha giữa u và i.
Đề bài cho điện áp uAM chính là điện áp hai đầu R, vì uR cùng pha với cường độ dòng điện i, nên ta có giản đồ vecto khi C = C1 là:
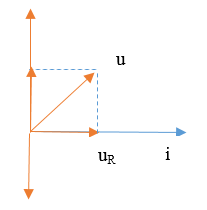
Khi C = C2 ta có
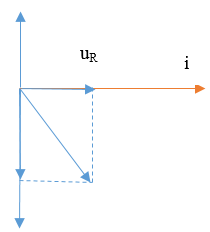
Độ lệch pha của cường độ dòng điện trong hai lần là:
\(\Delta {\varphi _{\left( {{i_1};{i_2}} \right)}} = \frac{\pi }{4} + \frac{\pi }{3} = \frac{{7\pi }}{{12}}\)
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
\cos {\varphi _1} = \frac{{{U_{R1}}}}{U} \Rightarrow {\varphi _1} = {\rm{arc}}\cos \frac{{{U_{R1}}}}{U}\\
\cos {\varphi _2} = \frac{{{U_{R2}}}}{U} \Rightarrow {\varphi _2} = {\rm{arc}}\cos \frac{{{U_{R2}}}}{U}
\end{array} \right.\\
\Rightarrow \arccos \frac{{{U_{R1}}}}{U} + \arccos \frac{{{U_{R2}}}}{U} = \frac{{7\pi }}{{12}}
\end{array}\)
Thay số và bấm máy tính tìm U:
\(\arccos \frac{{126}}{{\sqrt 2 U}} + {\rm{ar}}\cos \frac{{77}}{{\sqrt 2 U}} = \frac{{7\pi }}{{12}}\)
Ta được
\(U = 119,9V \approx 120V\)
Vậy U gần nhất với giá trị 115V.
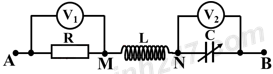
Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB như hình vẽ. Biết cuộn dây L thuần cảm, tụ điện có điện dung C thay đổi được. Các vôn kế V1, V2 lý tưởng. Điều chỉnh giá trị của C thì thấy ở cùng thời điểm số chỉ của V1 cực đại thì số chỉ của V1 gấp đôi số chỉ của V2. Hỏi khi số chỉ của V2 cực đại và có giá trị V2max = 200 V thì số chỉ của V1 là
-
A
80 V.
-
B
100 V.
-
C
120 V.
-
D
50 V.
Đáp án của giáo viên lời giải hay : A
+ Bài toán C biến thiên để \({U_{{R_{max}}}}\)
+ Bài toán C biến thiên để \({U_{{C_{max}}}}\)
+ Khi \(C = {C_0}\) thì: \({V_{1max}}\) khi đó mạch xảy ra cộng hưởng
\({V_{1max}} = {U_R} = {U_{AB}}\) và \({Z_L} = {Z_{{C_0}}}\)
Tại đây, ta có: \({U_R} = 2{U_{{C_0}}} \Rightarrow {U_{{C_0}}} = \dfrac{{{U_{AB}}}}{2} = {U_L}\)
\( \Rightarrow {Z_L} = {Z_{{C_0}}} = \dfrac{R}{2}\)
+ Khi \(C = C'\) thì \({V_{2max}}\) khi đó \({V_{2max}} = {U_{{C_{max}}}} = \dfrac{{{U^2}\sqrt {{R^2} + Z_L^2} }}{R}\) (1)
Và \({Z_{C'}} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}} = \dfrac{{{R^2} + \dfrac{{{R^2}}}{4}}}{{\dfrac{R}{2}}} = \dfrac{5}{2}R\)
Thay vào (1) ta có: \(200 = \dfrac{{U\sqrt {{R^2} + \dfrac{{{R^2}}}{4}} }}{R} \Rightarrow U = 80\sqrt 5 V\)
Số chỉ vôn kế \({V_1}\) khi đó là \({V_1} = {U_R} = I.R = \dfrac{U}{Z}.R\)
\({V_1} = \dfrac{{80\sqrt 5 }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_{C'}}} \right)}^2}} }}R = \dfrac{{80\sqrt 5 }}{{\sqrt {{R^2} + {{\left( {\dfrac{R}{2} - \dfrac{5}{2}R} \right)}^2}} }}R = 80V\)
Đặt điện áp \(u = 200\sqrt 2 \cos 100\pi t\,\,\left( V \right)\) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắc nối tiếp với đoạn mạch MB, trong đó đoạn mạch AM chứa cuộn dây điện trở r = 20 Ω, đoạn mạch MB chứa điện trở thuần R = 50 Ω nối tiếp với tụ điện có điện dung C thay đổi. Khi \(C = {C_1} = \dfrac{{200}}{\pi }\,\,\mu F\) thì trong mạch xảy ra hiện tượng cộng hưởng. Điều chỉnh \(C = {C_2}\) thì \({U_{MB\max }}\), giá trị cực đại đó xấp xỉ bằng
-
A
323,6 V
-
B
262,6 V
-
C
225,8 V
-
D
283,8 V
Đáp án của giáo viên lời giải hay : B
Mạch có cộng hưởng: \({Z_L} = {Z_C}\)
Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch MB: \({U_{MB}} = {U_{RC}} = \dfrac{{U.\sqrt {{R^2} + {Z_C}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Mạch xảy ra cộng hưởng, ta có:
\({Z_L} = {Z_{{C_1}}} \Rightarrow {Z_L} = \dfrac{1}{{\omega {C_1}}} = \dfrac{1}{{100\pi .\dfrac{{{{200.10}^{ - 6}}}}{\pi }}} = 50\,\,\left( \Omega \right)\)
Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch MB là:
\(\begin{array}{l}{U_{MB}} = {U_{RC}} = \dfrac{{U.\sqrt {{R^2} + {Z_C}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ \Rightarrow {U_{MB}} = \dfrac{{U.\sqrt {{{50}^2} + {Z_C}^2} }}{{\sqrt {{{70}^2} + {{\left( {50 - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{{{70}^2} - 100{Z_C}}}{{{{50}^2} + {Z_C}^2}}} }}\end{array}\)
Đặt \({Z_C} = x;y = \dfrac{{{{70}^2} - 100{Z_C}}}{{{{50}^2} + {Z_C}^2}} = \dfrac{{{{70}^2} - 100x}}{{{{50}^2} + {x^2}}} \Rightarrow {U_{MB}} = \dfrac{U}{{\sqrt {1 + y} }}\)
Để \({U_{MB\max }} \Leftrightarrow {y_{\min }} \Leftrightarrow y' = 0\)
Ta có: \(y' = \dfrac{{ - 100.\left( {{{50}^2} + {x^2}} \right) - 2x.\left( {{{70}^2} - 100x} \right)}}{{{{\left( {{{50}^2} + {x^2}} \right)}^2}}}\)
\(\begin{array}{l}y' = 0 \Leftrightarrow - 100.\left( {{{50}^2} + {x^2}} \right) - 2x.\left( {{{70}^2} - 100x} \right) = 0\\ \Rightarrow 100{x^2} - {2.70^2}x - {100.50^2} = 0\\ \Rightarrow \left[ \begin{array}{l}x = 119\,\,\left( \Omega \right)\\x = - 21\,\,\left( {loai} \right)\end{array} \right.\\ \Rightarrow {U_{MB\max }} = \dfrac{{200.\sqrt {{{50}^2} + {{119}^2}} }}{{\sqrt {{{70}^2} + {{\left( {50 - 119} \right)}^2}} }} \approx 262,6\,\,\left( V \right)\end{array}\)
Cho đoạn mạch AB gồm biến trở R, cuộn dây không thuần cảm với độ tự cảm \(L = \dfrac{{0,6}}{\pi }H\), điện trở \(r > 10\Omega \), tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 3}}}}{{3\pi }}F\) mắc nối tiếp. Đặt điện áp xoay chiều \(u = U\sqrt 2 cos100\pi t\left( V \right)\) (t tính bằng s) với \(U\) không đổi vào hai đầu A, B. Thay đổi giá trị biến trở R ta thu được đồ thị phụ thuộc của công suất tiêu thụ trên mạch vào giá trị R theo đường (1). Nối tắt cuộn dây và tiếp tục thì được đồ thị (2) biểu diễn sự phụ thuộc của công suất trên mạch vào giá trị R. Tỉ số \(\dfrac{{{R_0}}}{r}\) có giá trị là
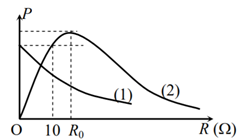
-
A
\(\dfrac{1}{4}.\)
-
B
\(4.\)
-
C
\(\dfrac{1}{3}.\)
-
D
\(3.\)
Đáp án của giáo viên lời giải hay : C
Sử dụng kĩ năng đọc đồ thị
Công suất: \(P = \dfrac{{{U^2}\left( {R + r} \right)}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Cảm kháng của cuộn dây là: \({Z_L} = \omega L = 100\pi .\dfrac{{0,6}}{\pi } = 60\,\,\left( \Omega \right)\)
Dung kháng của tụ điện là: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 3}}}}{{3\pi }}}} = 30\,\,\left( \Omega \right)\)
Khi chưa nối tắt cuộn dây: đồ thị (1)
Với \(R = 0 \Rightarrow {P_{1\max }} = \dfrac{{{U^2}\left( {R + r} \right)}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\,\,\left( 1 \right)\)
Khi nối tắt cuộn dây: đồ thị (2)
Ta có công suất: \({P_2} = \dfrac{{{U^2}R}}{{{R^2} + {Z_C}^2}}\)
Nhận xét: với \(R = 10\Omega \Rightarrow {P_2} = {P_{1\max }}\)
\(\begin{array}{l} \Rightarrow \dfrac{{{U^2}R}}{{{R^2} + {Z_C}^2}} = \dfrac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} \Rightarrow \dfrac{{10}}{{{{10}^2} + {{30}^2}}} = \dfrac{r}{{{r^2} + {{\left( {60 - 30} \right)}^2}}}\\ \Rightarrow 10{r^2} + 9000 = 1000r \Rightarrow 10{r^2} - 1000r + 9000 = 0\\ \Rightarrow \left[ \begin{array}{l}r = 10\,\,\left( \Omega \right)\,\,\left( {loai} \right)\\r = 90\,\,\left( \Omega \right)\,\,\left( {t/m} \right)\end{array} \right.\end{array}\)
Với \(R = {R_0} \Rightarrow {P_{2\max }} \Leftrightarrow {R_0} = {Z_C} = 30\,\,\left( \Omega \right)\)
Vậy \(\dfrac{{{R_0}}}{r} = \dfrac{{30}}{{90}} = \dfrac{1}{3}\)
Mạch điện RCL nối tiếp có C thay đổi được. Điện áp hai đầu đoạn mạch \(u = 200\sqrt 2 \cos 100\pi t\,\,\left( V \right)\). Khi \(C = {C_1} = \dfrac{{50}}{\pi }\,\,\mu F\) thì mạch tiêu thụ công suất cực đại \({P_{\max }} = 160\,\,{\rm{W}}\). Khi \(C = {C_2} = \dfrac{1}{{5\pi }}\,\,mF\) thì điện áp hai đầu đoạn mạch RC và cuộn dây vuông pha với nhau, điện áp hiệu dụng hai đầu cuộn dây khi đó gần giá trị nào nhất sau đây
-
A
90 V
-
B
120 V
-
C
75 V
-
D
140 V
Đáp án của giáo viên lời giải hay : D
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\)
Mạch có cộng hưởng: \({P_{\max }} = \dfrac{{{U^2}}}{{R + r}};\,\,{Z_L} = {Z_C}\)
Điện áp hiệu dụng giữa hai đầu cuộn dây: \({U_d} = \dfrac{{U.\sqrt {{r^2} + {Z_L}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Khi C = C1 và C = C2, dung kháng của tụ điện là:
\(\left\{ \begin{array}{l}{Z_{{C_1}}} = \dfrac{1}{{\omega {C_1}}} = \dfrac{1}{{100\pi .\dfrac{{{{50.10}^{ - 6}}}}{\pi }}} = 200\,\,\left( \Omega \right)\\{Z_{{C_2}}} = \dfrac{1}{{\omega {C_2}}} = \dfrac{1}{{100\pi .\dfrac{{{{1.10}^{ - 3}}}}{{5\pi }}}} = 50\,\,\left( \Omega \right)\end{array} \right.\)
Khi C = C1, trong mạch có cộng hưởng, khi đó:
\(\left\{ \begin{array}{l}{Z_L} = {Z_{{C_1}}} = 200\,\,\left( \Omega \right)\\{P_{\max }} = \dfrac{{{U^2}}}{{R + r}} \Rightarrow R + r = \dfrac{{{U^2}}}{{{P_{\max }}}} = \dfrac{{{{200}^2}}}{{160}} = 250\,\,\left( \Omega \right)\,\,\left( 1 \right)\end{array} \right.\)
Khi C = C2, uRC và urL vuông pha, ta có:
\(\begin{array}{l}\tan {\varphi _{{u_{RC}}}}.\tan {\varphi _{{u_{rL}}}} = - 1 \Rightarrow \dfrac{{ - {Z_{{C_2}}}}}{R}.\dfrac{{{Z_L}}}{r} = - 1\\ \Rightarrow R.r = {Z_{{C_2}}}.{Z_L} = 50.200 = 10000\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}R + r = 250\\R.r = 10000\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 200\,\,\left( \Omega \right)\\r = 50\,\,\left( \Omega \right)\end{array} \right.\)
Điện áp hiệu dụng giữa hai đầu cuộn dây là:
\(\begin{array}{l}{U_d} = \dfrac{{U.\sqrt {{r^2} + {Z_L}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_{{C_2}}}} \right)}^2}} }}\\ \Rightarrow {U_d} = \dfrac{{200.\sqrt {{{50}^2} + {{200}^2}} }}{{\sqrt {{{\left( {200 + 50} \right)}^2} + {{\left( {200 - 50} \right)}^2}} }} = 141\,\,\left( V \right)\end{array}\)
