Cho mạch điện không phân nhánh RLC: \(R = 80 Ω\) , cuộn dây có điện trở \(20 Ω\), có độ tự cảm \(L=0,636H\), tụ điện có điện dung \(C=31,8μF\). Hiệu điện thế hai đầu mạch là \(u = 200cos(100πt-\dfrac{\pi }{4}\)) (V) thì biểu thức cường độ dòng điện chạy qua mạch điện là:
-
A
\(i = \sqrt 2 cos(100\pi t - \dfrac{\pi }{2}){\text{ }}\left( A \right)\)
-
B
\(i = cos(100\pi t + \dfrac{\pi }{2}){\rm{ }}\left( A \right)\)
-
C
\(i = \sqrt 2 cos(100\pi t - \dfrac{\pi }{4}){\rm{ }}\left( A \right)\)
-
D
\(i = \sqrt 2 cos100\pi t{\rm{ }}\left( A \right)\)
Đáp án của giáo viên lời giải hay : A
Casio giải điện xoay chiều

Dòng điện chạy qua một đoạn mạch gồm cuộn dây thuần cảm có L = 1/10π (H), mắc nối tiếp với một tụ điện C = 2.10-4/π (F) có biểu thức \(i = 2\sqrt 2 \cos (100\pi t - \pi /6)\) (A). Biểu thức điện áp hai đầu mạch có thể là:
-
A
\(u = 80\sqrt 2 cos(100\pi t + \frac{\pi }{6}){\rm{ }}\left( V \right)\)
-
B
\(u = 80\sqrt 2 cos(100\pi t + \frac{\pi }{3}){\rm{ }}\left( V \right)\)
-
C
\(u = 80\sqrt 2 cos(100\pi t - \frac{{2\pi }}{3}){\rm{ }}\left( V \right)\)
-
D
\(u = 80\sqrt 2 \sin (100\pi t + \frac{\pi }{6}){\rm{ }}\left( V \right)\)
Đáp án của giáo viên lời giải hay : C
Casio giải điện xoay chiều

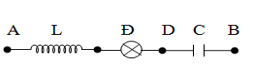
Mạch như hình vẽ.
Biết Đ: 100V – 100W ; L =\(\dfrac{1}{\pi }\)H , C = \(\dfrac{{50}}{\pi }\mu F\), uAD = 200\(\sqrt 2 \)sin 100πt+\(\dfrac{\pi }{6}\) )(V).
Biểu thức uAB có dạng:
-
A
200\(\sqrt 2 \)sin (100 πt + \(\dfrac{\pi }{4}\) )(V)
-
B
200 sin (100 πt – \(\dfrac{\pi }{4}\) )(V)
-
C
200\(\sqrt 2 \)sin (100 πt – \(\dfrac{\pi }{3}\) )(V)
-
D
200 sin (100 πt + \(\dfrac{\pi }{3}\) )(V)
Đáp án của giáo viên lời giải hay : C
Casio giải điện xoay chiều

Mạch như hình vẽ
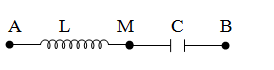
${u_{AB}} = 120\sqrt 2 cos\left( {100\pi t} \right)V$. Dùng vôn kế có điện trở rất lớn đo giữa $A$ và $M$ thì thấy nó chỉ $120V$, và $u_{AM}$ nhanh pha hơn $u_{AB}$ \(\dfrac{\pi }{2}\) . Biểu thức $u_{MB}$ có dạng:
-
A
\({u_{MB}} = 120\sqrt 2 \cos (100\pi t + \pi /2)\)(V)
-
B
\({u_{MB}} = 240\cos (100\pi t - \pi /4)\)(V)
-
C
\({u_{MB}} = 120\sqrt 2 \cos (100\pi t + \pi /4)\)(V)
-
D
\({u_{MB}} = 240\cos (100\pi t - \pi /2)\)(V)
Đáp án của giáo viên lời giải hay : B
Casio giải điện xoay chiều

Cho mạch điện xoay chiều gồm có R = 40Ω, cuộn dây thuần cảm có L = 1/2π(H) và tụ điện C. Điện áp hai đầu mạch u = 160cos100πt(V). Biết biểu thức cường độ dòng điện trong mạch là \(i = 2\sqrt 2 \cos (100\pi t + \pi /4)\) )(A). Tìm điện dung của tụ điện.
-
A
\(\frac{1}{{9000\pi }}\)
-
B
\(\frac{1}{{1000\pi }}\)
-
C
\(\frac{1}{{900\pi }}\)
-
D
\(\frac{1}{{100\pi }}\)
Đáp án của giáo viên lời giải hay : A
+ Cách 1 : Phương pháp đại số
+ Cách 2 : Phương pháp casio giải điện xoay chiều
+ Cách 1 : Phương pháp đại số
Cách A: Ta có : R = 40Ω, ZL = 50Ω
\(Z = \frac{{{U_0}}}{{{I_0}}} = \frac{{160}}{{2\sqrt 2 }} = 40\sqrt 2 = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \to \left| {{Z_L} - {Z_C}} \right| = 40 \to \left( \begin{array}{l}{Z_C} = 10\\{Z_C} = 90\end{array} \right.\)
Do I nhanh pha hơn u => ZC > ZL => ZC = 90 => C = 1/9000π (F)
Cách B : Độ lệch pha của u so với i : - π/4
\(\tan - \frac{\pi }{4} = \frac{{{Z_L} - {Z_C}}}{R} = - 1 \to {Z_C} = 90\Omega \to C = \frac{1}{{9000\pi }}F\)
+ Cách 2 : Phương pháp casio giải điện xoay chiều

Cho đoạn mạch xoay chiều như hình vẽ
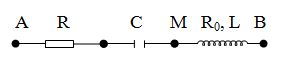
$R{\rm{ }} = {\rm{ }}50\Omega ,{\rm{ }}C = \dfrac{{{{2.10}^{ - 4}}}}{\pi }\left( F \right)$ , ${u_{AM}} = {\rm{ }}80cos100\pi t\left( V \right)$ , ${u_{MB}} = 200\sqrt 2 cos(100\pi t + \dfrac{\pi }{2})\left( V \right)$ . Giá trị của $R_0$ và $L$ là:
-
A
$250 Ω$ và $0,8H$
-
B
$250 Ω$ và $0,56H$
-
C
$176,8 Ω$ và $0,56H$
-
D
$176,8 Ω$ và $0,8H$
Đáp án của giáo viên lời giải hay : C
Phương pháp casio giải điện xoay chiều

Đoạn mạch AC có điện trở thuần, cuộn dây thuần cảm và tụ điện mắc nối tiếp. B là một điểm trên AC với \({u_{AB}} = \sin 100\pi t\left( V \right)\); \({u_{BC}} = \sqrt 3 \sin \left( {100\pi t - \dfrac{\pi }{2}} \right)\left( V \right)\) . Tính biểu thức hiệu điện thế uAC.
-
A
\({u_{AC}} = 2\sqrt 2 \sin \left( {100\pi t} \right)\left( V \right)\)
-
B
\({u_{AC}} = \sqrt 2 \sin \left( {100\pi t + \dfrac{\pi }{3}} \right)\left( V \right)\)
-
C
\({u_{AC}} = 2\sin \left( {100\pi t + \dfrac{\pi }{3}} \right)\left( V \right)\)
-
D
\({u_{AC}} = 2\sin \left( {100\pi t - \dfrac{\pi }{3}} \right)\left( V \right)\)
Đáp án của giáo viên lời giải hay : D
Casio giải điện xoay chiều
(Cộng các hiệu điện thế thành phần lại với nhau)
Chuyển uAB và uBC sang dạng số phức
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{{u_{AB}} = {\rm{ }}1}\\{{u_{BC}} = \sqrt 3 \angle - \dfrac{\pi }{2}}\end{array}} \right. \\\to {u_{AC}} = {u_{AB}} + {u_{BC}} = 1 + \sqrt 3 \angle - \dfrac{\pi }{2} = 2\angle - \dfrac{\pi }{3}\\ \to {u_{AC}} = 2\sin \left( {100\pi t - \dfrac{\pi }{3}} \right)\end{array}\)
Mạch điện nối tiếp R, L, C trong đó cuộn dây thuần cảm (ZL < ZC). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = 200\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{4}} \right)V\). Khi \(R = 50Ω\) công suất mạch đạt giá trị cực đại. Biểu thức dòng điện qua mạch lúc đó:
-
A
\(i = 4c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
B
\(i = 4c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{4}} \right)A\)
-
C
\(i = 4\sqrt 2 c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
D
\(i = 4\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)A\)
Đáp án của giáo viên lời giải hay : A
Casio giải điện xoay chiều
Ta có, khi R = 50Ω công suất mạch đạt giá trị cực đại
\( \to \left| {{Z_L} - {Z_C}} \right| = R = 50\Omega \)
Do ZL < ZC => ZL - ZC = -50
\(\begin{array}{l}i = \dfrac{u}{Z} = \dfrac{{200\sqrt 2 \angle \dfrac{\pi }{4}}}{{50 - 50i}} = 4\angle \dfrac{\pi }{2}\\ \to i = 4c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\end{array}\)
Cho mạch điện như hình vẽ. \(R = 50\,(\Omega ),\,\,L = \frac{1}{\pi }(H)\). Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều \(u = 220\sqrt 2 \sin \left( {100\pi t} \right)\,\,(V)\). Biết tụ điện có điện dung C thay đổi được. Tính C để hiệu điện thế cùng pha cường độ dòng điện.
-
A
\(\frac{{{{10}^{ - 5}}}}{{2\pi }}F\)
-
B
\(\frac{{{{10}^{ - 3}}}}{\pi }F\)
-
C
\(\frac{{{{10}^{ - 3}}}}{{2\pi }}F\)
-
D
\(\frac{{{{10}^{ - 4}}}}{\pi }F\)
Đáp án của giáo viên lời giải hay : D
+ Cách 1: Phương pháp đại số
+ Cách 2: Phương pháp casio giải điện xoay chiều
+ Cách 1:
Ta có: hiệu điện thế cùng pha với cường độ dòng điện => Mạch cộng hưởng dao động
=> ZL = ZC = 100Ω
=> C = 1/1000π F
+ Cách 2:
Biểu diễn các đại lượng dưới dạng số phức:
\({u_{AB}} = 220\sqrt 2 \,\)
\({Z_L} = L\omega = \frac{1}{\pi } \cdot 100\pi = 100\,\,(\Omega )\)
\(Z_{AB}^{} = R + \left( {{Z_L} - {Z_C}} \right)i = 50 + \left( {100 - {Z_C}} \right)i\)
Ta có:
\({i_{AB}} = \frac{{{u_{AB}}}}{{Z_{AB}^{}}} = 220\sqrt 2 :\left( {50 + \left( {100 - {Z_C}} \right)i} \right)\)
Để hiệu điện thế cùng pha với cường độ dòng điện thì i = I0. Khi đó, thành phần ảo trong tổng trở Z phải bằng 0
\( \Rightarrow 100 - {Z_C} = 0 \Rightarrow \,\,{Z_C} = 100\,\,\)mà \(\,{Z_C} = \frac{1}{{C\omega }}\)
\( \Rightarrow C = \frac{1}{{{Z_C}\omega }} = \frac{1}{{100 \cdot 100\pi }} = \frac{{{{10}^{ - 4}}}}{\pi }\,\,(F)\)
Đặt một điện áp xoay chiều vào hai đầu một cuộn dây chỉ có độ tự cảm L = \(\frac{1}{{2\pi }}H\) thì cường độ dòng điện qua cuộn dây có biểu thức : \(i{\rm{ }} = {\rm{ }}3\sqrt 2 {\rm{cos}}\left( {100\pi t + \frac{\pi }{6}} \right)\) (A). Nếu đặt điện áp nói trên vào hai bản tụ của tụ điện có điện dung \(C{\rm{ }} = \frac{1}{\pi }{.10^{ - 4}}\)F thì biểu thức nào trong các biểu thức sau đúng với biểu thức dòng điện ?
-
A
\(i{\rm{ }} = {\rm{ }}1,5\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{{5\pi }}{6}} \right)\) (A).
-
B
\(i{\rm{ }} = {\rm{ }}1,5{\rm{cos}}\left( {100\pi t + \frac{{5\pi }}{6}} \right)\) (A).
-
C
\(i{\rm{ }} = {\rm{ }}1,5\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{{7\pi }}{6}} \right)\) (A).
-
D
\(i{\rm{ }} = {\rm{ }}1,5{\rm{cos}}\left( {100\pi t - \frac{{7\pi }}{6}} \right)\) (A).
Đáp án của giáo viên lời giải hay : A
Casio giải điện xoay chiều:
\(\begin{array}{l}u = {i_1}{Z_L}\\ \to {i_2} = \frac{u}{{{Z_C}}} = \frac{{{i_1}{Z_L}}}{{{Z_C}}} = 3\sqrt 2 \angle \frac{\pi }{6}x\left( {50i} \right):\left( { - 100i} \right) = 1,5\sqrt 2 \angle - \frac{{5\pi }}{6}\\ \to {i_2} = 1,5\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{{5\pi }}{6}} \right)\end{array}\)
Một đoạn mạch gồm một tụ điện có dung kháng ZC = 100Ω cuộn dây có cảm kháng ZL=200\(\Omega \) mắc nối tiếp nhau. Điện áp tại hai đầu cuộn cảm có dạng \({{\rm{u}}_{\rm{L}}}{\rm{ = 100cos(100\pi t + }}\dfrac{{\rm{\pi }}}{{\rm{6}}}{\rm{)V}}\). Biểu thức điện áp ở hai đầu tụ điện có dạng là:
-
A
\({{\rm{u}}_{\rm{C}}}{\rm{ = 100cos(100\pi t + }}\dfrac{{\rm{\pi }}}{{\rm{6}}}{\rm{)V}}\)
-
B
\({{\rm{u}}_{\rm{C}}}{\rm{ = 50cos(100\pi t - }}\dfrac{{\rm{\pi }}}{{\rm{3}}}{\rm{)V}}\)
-
C
\({{\rm{u}}_{\rm{C}}}{\rm{ = 100cos(100\pi t - }}\dfrac{{\rm{\pi }}}{{\rm{2}}}{\rm{)V}}\)
-
D
\({{\rm{u}}_{\rm{C}}}{\rm{ = 50cos(100\pi t - }}\dfrac{{{\rm{5\pi }}}}{{\rm{6}}}{\rm{)V}}\)
Đáp án của giáo viên lời giải hay : D
Casio giải điện xoay chiều:
\({u_C} = i{Z_C} = \dfrac{{{u_L}}}{{{Z_L}}}{Z_C} \\= 100\angle \dfrac{\pi }{6}:(200i)x( - 100i) \\= 50\angle - \dfrac{{5\pi }}{6}\)
=> Biểu thức giữa hai đầu tụ điện: \(u_C=50cos(100\pi t - \dfrac{5\pi}{6})V\)
Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần và một cuộn cảm thuần mắc nối tiếp mộ điện áp xoay chiều có biểu thức \(u = 100\sqrt 2 c{\rm{os}}\left( {\omega t + \frac{{7\pi }}{{12}}} \right)V\) thì khi đó điện áp hai đầu điện trở thuần có biểu thức \({u_R} = 100c{\rm{os}}\left( {\omega t + \frac{\pi }{3}} \right)V\) . Biểu thức điện áp giữa hai đầu cuộn cảm thuần sẽ là:
-
A
${u_L} = 100c{\text{os}}\left( {\omega t + \frac{\pi }{6}} \right)V$
-
B
${u_L} = 100\sqrt 2 c{\text{os}}\left( {\omega t + \frac{{5\pi }}{6}} \right)V$
-
C
${u_L} = 100c{\text{os}}\left( {\omega t + \frac{{5\pi }}{6}} \right)V$
-
D
${u_L} = 100\sqrt 2 c{\text{os}}\left( {\omega t + \frac{{\pi }}{6}} \right)V$
Đáp án của giáo viên lời giải hay : C
Casio giải điện xoay chiều
Ta có:
\(\begin{array}{l}u = {u_R} + {u_L} \to {u_L} = u - {u_R} = 100\sqrt 2 \angle \frac{{7\pi }}{{12}} - 100\angle \frac{\pi }{3} = 100\angle \frac{{5\pi }}{6}\\ \to {u_L} = 100c{\rm{os}}\left( {\omega t + \frac{{5\pi }}{6}} \right)V\end{array}\)
Cho đoạn mạch xoay chiều không phân nhánh gồm điện trở thuần R, cuộn dây thuần cảm L; tụ điện có điện dung C. Đặt vào 2 đầu đoạn mạch một điện áp xoay chiều thì điện áp tức thời giữa hai đầu điện trở là: \({u_R} = 100c{\rm{os}}\left( {100\pi t + \frac{\pi }{4}} \right)V\), giữa hai đầu cuộn cảm thuần là: \({u_L} = 120c{\rm{os}}\left( {100\pi t + \frac{{3\pi }}{4}} \right)V\), giữa hai đầu tụ điện là \({u_C} = 20c{\rm{os}}\left( {100\pi t - \frac{\pi }{4}} \right)V\). Biểu thức giữa hai đầu đoạn mạch là:
-
A
\({u_{AB}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{\pi }{2}} \right)V\)
-
B
\({u_{AB}} = 240{\rm{cos}}\left( {100\pi t - 1,43} \right)V\)
-
C
\({u_{AB}} = 240{\rm{cos}}\left( {100\pi t + 1,43} \right)V\)
-
D
\({u_{AB}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)V\)
Đáp án của giáo viên lời giải hay : D
Casio giải điện xoay chiều
Ta có:
\(\begin{array}{l}u = {u_R} + {u_L} + {u_C} \to u = 100\angle \frac{\pi }{4} + 120\angle \frac{{3\pi }}{4} + 20\angle - \frac{\pi }{4} = 100\sqrt 2 \angle \frac{\pi }{2}\\ \to u = 100\sqrt 2 c{\rm{os}}\left( {\omega t + \frac{\pi }{2}} \right)V\end{array}\)
Đặt điện áp xoay chiều \({u_{AB}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)V\) vào mạch RLC nối tiếp theo thứ tự là điện trở R, cuộn dây thuần cảm có L thay đổi được và \(C\). Khi \(L =L_1= 1/π H\) hay \(L =3L_1\) thì mạch có cùng công suất nhưng dòng điện i1 và i2 lệch pha nhau \(\dfrac{2\pi}{3}\). Biểu thức của hiệu điện thế uMB (M là điểm nằm giữa cuộn dây và tụ điện) khi L = L1 là:
-
A
\({u_{MB}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{{2\pi }}{3}} \right)V\)
-
B
\({u_{MB}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{{2\pi }}{3}} \right)V\)
-
C
\({u_{MB}} = 244,95{\rm{cos}}\left( {100\pi t - \dfrac{\pi }{6}} \right)V\)
-
D
\({u_{MB}} = 50\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{2}} \right)V\)
Đáp án của giáo viên lời giải hay : C
Casio giải điện xoay chiều
Cảm kháng:
\({Z_{{L_1}}} = \omega {L_1} = 100\Omega \)
Mạch có L thay đổi mà có cùng công suất P thì:
\(\left\{ \begin{array}{l}{Z_C} = \dfrac{{{Z_{{L_1}}} + {Z_{{L_2}}}}}{2} = 2{Z_{{L_1}}} = 200\Omega \\{\varphi _{{i_1}/{i_2}}} = 2\alpha = \dfrac{{2\pi }}{3}\end{array} \right. \\\to {\varphi _1} = \dfrac{\pi }{3} \\\to R = \dfrac{{{Z_{{L_1}}}}}{{\sqrt 3 }} = \dfrac{{100}}{{\sqrt 3 }}\Omega \)
Điện áp:
\(\begin{array}{l}{u_{MB}} = i.{Z_{MB}} = \dfrac{u}{Z}{Z_{MB}} = 100\sqrt 2 \div \left( {\dfrac{{100}}{{\sqrt 3 }} + \left( {100 - 200} \right)i} \right)x( - 200i)\\ = 244,9489743\angle - \dfrac{\pi }{6}\end{array}\)
Đoạn mạch xoay chiều AB gồm đoạn mạch AM nối tiếp với MB. Cho dòng điện có cường độ \(i = 2\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{\pi }{6}} \right)A\) chạy qua mạch, thì điện áp giữa 2 đầu các đoạn mạch AM, MB có biểu thức lần lượt là:
\({u_{AM}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{\pi }{2}} \right)V;{u_{MB}} = 100\sqrt 6 {\rm{cos}}\left( {100\pi t - \frac{\pi }{3}} \right)V\). Công suất tiêu thụ của đoạn mạch AB bằng:
-
A
315 W
-
B
400 W
-
C
300 W
-
D
350 W
Đáp án của giáo viên lời giải hay : B
Casio giải điện xoay chiều
Hiệu điện thế giữa hai đầu đoạn mạch AB:
\(\begin{array}{l}{u_{AB}} = {u_{AM}} + {u_{MB}} = 100\sqrt 2 \angle - \frac{\pi }{2} + 100\sqrt 6 \angle - \frac{\pi }{3}\\ = 374,166\angle - 1,237\\ \to P = UIc{\rm{os}}\varphi {\rm{ = }}\frac{{374,166.2\sqrt 2 }}{{\sqrt 2 \sqrt 2 }}{\rm{cos}}\left( { - 1,237 - \left( { - \frac{\pi }{6}} \right)} \right) = 400,11{\rm{W}}\end{array}\)
Đoạn mạch AB theo thứ tự gồm cuộn dây , điện trở và tụ điện có điện dung C mắc nối tiếp. Gọi M là điểm nối giữa cuộn dây và điện trở R. Đặt vào hai đầu đoạn mạch AB điện áp xoay chiều ổn định. Khi đó điện áp hai đầu AM và MB có biểu thức \({u_{AM}} = 100\cos \left( {100\pi t + \dfrac{\pi }{7}} \right)\left( V \right)\); \({u_{MB}} = 100\sqrt 3 \cos \left( {100\pi t - \dfrac{{5\pi }}{{14}}} \right)\left( V \right)\) . Tại thời điểm điện áp hai đầu AM có giá trị gấp đôi điện áp hai đầu MB thì điện áp hai đầu đoạn mạch AB có độ lớn xấp xỉ là
-
A
288,2V
-
B
144,1V
-
C
173,2V
-
D
196,4V
Đáp án của giáo viên lời giải hay : B
Sử dụng máy tính bỏ túi CASIO cho đoạn mạch xoay chiều
Cách giải :
\({u_{AB}} = {u_{AM}} + {u_{MB}} = > \overline {{u_{AB}}} = \overline {{u_{AM}}} + \overline {{u_{MB}}} = 100\angle \dfrac{\pi }{7} + 100\sqrt 3 \angle \dfrac{{ - 5\pi }}{{14}} = 200\angle - \dfrac{{4\pi }}{{21}}\)
Mà
\(\eqalign{& U_0^2 = U_{0AM}^2 + U_{0MB}^2 = > \overrightarrow {{U_{AM}}} \bot \overrightarrow {{U_{MB}}} = > {\left( {{{{u_{AM}}} \over {{U_{0AM}}}}} \right)^2} + {\left( {{{{u_{MB}}} \over {{U_{0MB}}}}} \right)^2} = 1 \cr & \buildrel {{u_{AM}} = 2{u_{MB}}} \over\longrightarrow {\left( {{{2{u_{MB}}} \over {100}}} \right)^2} + {\left( {{{{u_{MB}}} \over {100\sqrt 3 }}} \right)^2} = 1 = > \left\{ \matrix{{u_{AM}} \approx 96,0 \hfill \cr {u_{MB}} \approx 48,0 \hfill \cr} \right. = > {u_{AB}} \approx 144V \cr} \)
