Công suất tỏa nhiệt của dòng điện xoay chiều được tính theo công thức:
-
A
\(P = UI\sin \varphi \)
-
B
\(P = UI\cos \varphi \)
-
C
\(P = UI\)
-
D
\(P = ui\cos \varphi \)
Đáp án của giáo viên lời giải hay : B
Công suất của dòng điện xoay chiều được tính theo công thức:
\(P = UI\cos \varphi \)
Trong đoạn mạch RLC nối tiếp, gọi Z là tổng trở của mạch thì hệ số công suất của đoạn mạch được tính bởi:
-
A
\(cos\varphi = \dfrac{Z}{{\sqrt {{R^2} + {Z^2}} }}\)
-
B
\(cos\varphi = \dfrac{Z}{R}\)
-
C
cosφ = \(\dfrac{R}{{\sqrt {{R^2} + {Z^2}} }}\)
-
D
\(cos\varphi = \dfrac{R}{Z}\)
Đáp án của giáo viên lời giải hay : D
Hệ số công suất của đoạn mạch: \(cos\varphi = \dfrac{R}{Z}\)
Mạch điện xoay chiều nào sau đây có hệ số công suất lớn nhất. Với R là điện trở thuần, L là độ tự cảm, C là điện dung:
-
A
Mạch chỉ có R
-
B
Mạch nối tiếp L và C.
-
C
Mạch chỉ có C
-
D
Mạch nối tiếp R và L.
Đáp án của giáo viên lời giải hay : A
Vận dụng biểu thức tính hệ số công suất của mạch điện xoay chiều:\({\rm{cos}}\varphi {\rm{ = }}\frac{R}{Z}\)
Ta có: \({\rm{cos}}\varphi {\rm{ = }}\frac{R}{Z}\)
=> Mạch chỉ có R hoặc mạch có RLC mắc nối tiếp trong đó ZL = ZC thì cho hệ số công suất lớn nhất bằng 1
Công suất của một đoạn mạch RLC nối tiếp có tính dung kháng (ZL < ZC). Nếu ta tăng tần số của dòng điện thì hệ số công suất của mạch:
-
A
Không thay đổi.
-
B
Giảm
-
C
Tăng
-
D
Tăng lên rồi giảm
Đáp án của giáo viên lời giải hay : D
Ta có, hệ số công suất:
\({\rm{cos}}\varphi {\rm{ = }}\dfrac{R}{Z} = k\)
Mạch có tính dung kháng: ZL < ZC
Khi ta tăng tần số của dòng điện thì khi đó:
+ Hiệu số cảm kháng và dung kháng giảm dần về 0, khi đó hệ số công suất tăng dần đến k0
+ Sau đó hiệu số cảm kháng và dung kháng tăng dần từ 0 đến giá trị nào đó=> hệ số công suất k giảm từ k0
=> Chọn D - k tăng lên rồi giảm
Công suất của một đoạn mạch R, L, C nối tiếp không phụ thuộc vào:
-
A
Độ tự cảm L của mạch điện.
-
B
Pha ban đầu \(\varphi \) của dòng điện qua mạch.
-
C
Chu kì T của điện áp hai đầu đoạn mạch
-
D
Dung kháng ZC của mạch điện.
Đáp án của giáo viên lời giải hay : B
Ta có: Công suất
\(P = UIcos\varphi = {\rm{ }}UI\dfrac{R}{Z} = \dfrac{U}{Z}IR = {I^2}R\)
=> Công suất không phụ thuộc vào pha ban đầu của dòng điện qua mạch.
Một mạch điện RLC nối tiếp có \(C = 1/({\omega ^2}L)\). Nếu ta tăng dần giá trị của C thì:
-
A
Công suất của mạch tăng.
-
B
Công suất của mạch giảm
-
C
Công suất của mạch không đổi
-
D
Công suất của mạch tăng lên rồi giảm.
Đáp án của giáo viên lời giải hay : B
Theo đầu bài, ta có:
+ \(C = 1/({\omega ^2}L) \leftrightarrow {Z_L} = {Z_C}\)
khi đó công suất trong mạch đạt giá trị cực đại:
\({P_{{\rm{max}}}} = \dfrac{{{U^2}}}{R}\)
+ Khi tăng dần giá trị của C => tổng trở của mạch tăng => công suất của mạch giảm
Đoạn mạch RLC nối tiếp có hệ số công suất lớn nhất. Hệ thức nào sau đây không đúng:
-
A
$P = U.I$
-
B
\(T = 2\pi \sqrt {L.C} \)
-
C
$Z = R$
-
D
\(U = {U_L} = {U_C}\)
Đáp án của giáo viên lời giải hay : D
Ta có, mạch RLC mắc nối tiếp có hệ số công suất lớn nhất khi:
\({Z_L} = {Z_C}\)
Khi đó, ta có:
+ \(\omega = \frac{1}{{\sqrt {LC} }} \to T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {LC} \)
+ Công suất cực đại:
\({P_{{\rm{max}}}} = UI\)
+ Tổng trở khi đó:
\(Z = R\)
+ \(U = {U_R}\)
=> Phương án D - sai
Một mạch điện xoay chiều RLC nối tiếp. Điện áp ở hai đầu đoạn mạch \(u = {U_0}\cos \omega t\), cho biết \(LC{\omega ^2} = 1\). Nếu ta tăng tần số góc \(\omega \) của u thì
-
A
Công suất tiêu thụ của mạch điện tăng
-
B
Cường độ hiệu dụng qua mạch giảm
-
C
Tổng trở của đoạn mạch giảm
-
D
Hệ số công suất của mạch tăng.
Đáp án của giáo viên lời giải hay : B
Theo đầu bài, ta có:
\(LC{\omega ^2} = 1 \to {Z_L} = {Z_C}\)
=> Công suất của mạch cực đại
Nếu ta tăng tần số góc \(\omega \)thì:
+ Công suất tiêu thụ của mạch giảm
+ Cường độ hiệu dụng qua mạch giảm:
\(I = \frac{U}{Z}\)
+ Tổng trở của đoạn mạch tăng
+ Hệ số công suất của mạch giảm
Ta suy ra:
A, C, D - sai
B- đúng
Đoạn mạch điện xoay chiều có điện áp ở hai đầu \(u = 100\cos \left( {100\pi t + \pi /2} \right)(V)\) và dòng điện xoay chiều qua mạch \(i = 2\cos \left( {100\pi t + \pi /6} \right)(A)\). Công suất tiêu thụ của mạch điện là:
-
A
200 W
-
B
100 W
-
C
50 W
-
D
86,6 W
Đáp án của giáo viên lời giải hay : C
Áp dụng biểu thức xác định công suất tiêu thụ của mạch điện: \(P = UIcos\varphi \)
Ta có:
+ Độ lệch pha giữa u và i:
\(\varphi = \dfrac{\pi }{2} - \dfrac{\pi }{6} = \dfrac{\pi }{3}(ra{\rm{d}})\)
+ Công suất tiêu thụ của mạch điện:
\(P = UIcos\varphi = \dfrac{{100}}{{\sqrt 2 }}.\dfrac{2}{{\sqrt 2 }}.c{\rm{os}}\dfrac{\pi }{3} = 50{\rm{W}}\)
Đoạn mạch nối tiếp có \(R = 80\Omega \); \(L = 0,4/\pi (H)\)và \(C = {10^{ - 4}}/\pi (F)\). Mắc mạch điện vào nguồn \(220V – 50 Hz\). Công suất toả nhiệt của đoạn mạch là:
-
A
605 W
-
B
484W
-
C
176W
-
D
387,2W
Đáp án của giáo viên lời giải hay : D
+ Áp dụng công thức tính cảm kháng, dung kháng: \({Z_L} = \omega L;{Z_C} = \dfrac{1}{{\omega C}}\)
+ Áp dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)
+ Áp dụng biểu thức xác định công suất tiêu thụ của mạch điện: \(P = {I^2}R\)
Ta có:
+ Cảm kháng:
\({Z_L} = \omega L = 2\pi fL = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega \)
+ Dung kháng:
\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
+ Tổng trở của mạch:
\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{{80}^2} + {{(40 - 100)}^2}} = 100\Omega \)
+ Cường độ dòng điện hiệu dụng trong mạch:
\(I = \dfrac{U}{Z} = \dfrac{{220}}{{100}} = 2,2(A)\)
+ Công suất tỏa nhiệt :
\(P = {I^2}R = {2,2^2}.80 = 387,2{\rm{W}}\)
Mạch điện RLC nối tiếp được mắc vào mạng điện \(100 V – 50 Hz\). Cho biết công suất của mạch điện là \(30 W\) và hệ số công suất là \(0,6\). Giá trị của R là:
-
A
\(60\Omega \)
-
B
\(333\Omega \)
-
C
\(120\Omega \)
-
D
\(100\Omega \)
Đáp án của giáo viên lời giải hay : C
+ Áp dụng biểu thức xác định công suất tiêu thụ của mạch điện: \(P = UIcos\varphi \)
+ Áp dụng công thức tính tổng trở: \(Z = \dfrac{U}{I}\)
+ Áp dụng công thức tính hệ số công suất: \({\rm{cos}}\varphi = \dfrac{R}{Z}\)
Ta có:
Công suất tiêu thụ của mạch điện:
\(P = UIcos\varphi \to I = \dfrac{P}{{Uc{\rm{os}}\varphi }} = \dfrac{{30}}{{100.0,6}} = 0,5(A)\)
Tổng trở :
\(Z = \dfrac{U}{I} = \dfrac{{100}}{{0,5}} = 200\Omega \)
Hệ số công suất :
\({\rm{cos}}\varphi {\rm{ = }}\dfrac{R}{Z} = 0,6 \to R = cos \varphi . Z =0,6.200 = 120\Omega \)
Cuộn dây có điện trở thuần \(R = 50\Omega \) và độ tự cảm L mắc vào điện áp xoay chiều \(U = 100 V\) và chu kì \(0,02s\). Cho biết công suất của mạch điện là \(100W\). Giá trị của L là:
-
A
\(2/\pi (H)\)
-
B
\(1/\pi (H)\)
-
C
\(0,5/\pi (H)\)
-
D
\(0,4/\pi (H)\)
Đáp án của giáo viên lời giải hay : C
+ Vận dụng biểu thức tính công suất: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ Vận dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)
+ Áp dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
Ta có:
+ công suất tiêu thụ của mạch điện:
\(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ Do mạch là cuộn dây có điện trở thuần và độ tự cảm L => tổng trở của mạch:
\(Z = \sqrt {{R^2} + {Z_L}^2} \)
\( \to P = \dfrac{{{U^2}}}{{{R^2} + Z_L^2}}R \leftrightarrow 100 = \frac{{{{100}^2}}}{{{{50}^2} + {Z_L}^2}}50 \to {Z_L} = 50\Omega \)
+ Mặt khác, ta có:
\({Z_L} = \omega L = \dfrac{{2\pi }}{T}L \to L = \dfrac{{{Z_L}.T}}{{2\pi }} = \dfrac{{50.0,02}}{{2\pi }} = \dfrac{{0,5}}{\pi }(H)\)
Một mạch điện nối tiếp có \(R = 60\Omega \), \(C = {10^{ - 3}}/(8\pi )(F)\) được mắc vào mạng điện xoay chiều 220 V – 50Hz. Hệ số công suất của mạch là:
-
A
0,6
-
B
0,4
-
C
0,8
-
D
1
Đáp án của giáo viên lời giải hay : A
+ Áp dụng công thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Áp dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)
+ Áp dụng công thức tính hệ số công suất: \({\rm{cos}}\varphi = \dfrac{R}{Z}\)
Ta có:
+ Dung kháng:
\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{{8\pi }}}} = 80\Omega \)
+ Tổng trở của mạch:
\(Z = \sqrt {{R^2} + {Z_C}^2} = \sqrt {{{60}^2} + {{80}^2}} = 100\Omega \)
+ hệ số công suất:
\({\rm{cos}}\varphi = \dfrac{R}{Z} = \dfrac{{60}}{{100}} = 0,6\)
Mạch điện xoay chiều RLC nối tiếp. Hai đầu đoạn mạch có một điện áp xoay chiều có tần số và điện áp hiệu dụng không đổi. Dùng vôn kế có điện trở rất lớn, lần lượt đo điện áp ở hai đầu đoạn mạch, hai đầu tụ điện và hai đầu cuộn dây thì số chỉ của vôn kế tương ứng là U, UC và UL. Biế U = UC = 2UL. Hệ số công suất của mạch là:
-
A
\(\cos \varphi = 0,5\)
-
B
\(\cos \varphi = \sqrt 3 /2\)
-
C
\(\cos \varphi = \sqrt 2 /2\)
-
D
\(\cos \varphi = 1\)
Đáp án của giáo viên lời giải hay : B
+ Áp dụng công thức tính hiệu điện thế hiệu dụng hai đầu đoạn mạch:
\(U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} \)
+ Áp dụng công thức tính hệ số công suất: \({\rm{cos}}\varphi = \frac{R}{Z}\)
Ta có:
+ \(\begin{array}{l}U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} \leftrightarrow {U^2} = U_R^2 + {(\frac{U}{2} - U)^2}\\ \to {U_R} = \frac{{\sqrt 3 U}}{2}\end{array}\)
+ Hệ số công suất:
\({\rm{cos}}\varphi = \frac{R}{Z} = \frac{{{U_R}}}{U} = \frac{{\frac{{\sqrt 3 U}}{2}}}{U} = \frac{{\sqrt 3 }}{2}\)
Đoạn mạch AB gồm hai đoạn AD và DB ghép nối tiếp. Điện áp tức thời trên các đoạn mạch và dòng điện qua chúng lần lượt có biểu thức: \({u_{AD}} = 100\sqrt 2 cos(100\pi t + \dfrac{\pi}{2})\left( V \right);\) \({u_{DB}} = 100\sqrt 6 cos(100\pi t + \dfrac{2\pi}{ 3})\left( V \right)\), \(i{\rm{ }} = \sqrt 2 cos(100\pi t + \dfrac{\pi}{2})\left( A \right).\)Công suất tiêu thụ của đoạn mạch AB là:
-
A
100W
-
B
242W
-
C
186,6W
-
D
250W
Đáp án của giáo viên lời giải hay : D
+ Sử dụng công thức tính công suất tiêu thụ: P=I2R
+ Từ độ lệch pha u,i: Xác định các thành phần có trong đoạn mạch, sử dụng công thức tính \(tan\varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Điện áp đoạn mạch \(AD\) cùng pha với i nên trên đoạn mạch \(AD\) chỉ có điện trở \(R\) hoặc \(RLC\) nhưng \(Z_L=Z_C\).
\( \to R = \dfrac{U}{I} = 100\Omega \)
Điện áp đoạn mạch \(BD\) sớm pha hơn i một góc \(\varphi = \dfrac{\pi }{6}\)
=> Trên đoạn mạch \(BD\) có điện trở \(R'\) và X (X có thể là \({Z_L}\) hoặc \({Z_L}\) và \({Z_C}\) \(\left( {{Z_L} > {Z_C}} \right)\)
\(\begin{array}{l} \to \tan \dfrac{\pi }{6} = \dfrac{{{Z_X}}}{{R'}} = \dfrac{1}{{\sqrt 3 }} \to {Z_X} = \dfrac{{R'}}{{\sqrt 3 }}\\ \to {Z_{BD}} = \dfrac{{{U_{BD}}}}{I} = 100\sqrt 3 \end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}{Z_{BD}} = \sqrt {R{'^2} + Z_X^2} = \sqrt {R{'^2} + \dfrac{{R{'^2}}}{3}} = \dfrac{{2R'}}{{\sqrt 3 }} = 100\sqrt 3 \\ \Rightarrow R' = 150\Omega \end{array}\)
=> Công suất tiêu thụ của đoạn mạch AB là: \(P = {I^2}(R + R') = 1(100 + 150) = 250W\)
Đặt vào 2 đầu mạch điện có 2 phần tử C và R với điện trở R = ZC = 100 một nguồn điện tổng hợp có biểu thức \(u{\rm{ }} = 100{\rm{ }} + {\rm{ }}100\sqrt 2 cos(100\pi t + {\rm{ }}\pi {\rm{ }}/4)\) V. Tính công suất tỏa nhiệt trên điện trở:
-
A
50W
-
B
200W
-
C
25W
-
D
150W
Đáp án của giáo viên lời giải hay : A
+ Sử dụng công thức tính công suất tiêu thụ: P = I2R
+ Xác định các thành phần trong biểu thức của hiệu điện thế u: phần xoay chiều, phần một chiều.
+ Tụ điện không cho dòng một chiều đi qua.
Hiệu điện thế của đoạn mạch là tổng hợp của 2 thành phần:
+ Phần không đổi: U’=100V phần này không tạo ra dòng điện vì đoạn mạch chứa C ( Tụ điện không cho dòng điện không đổi đi qua)
+ Phần xoay chiều:
\(u = 100\sqrt 2 {\rm{cos(100}}\pi {\rm{t + }}\frac{\pi }{4})V\)
Tổng trở của đoạn mạch là:
\(Z = 100\sqrt 2 \to I = \frac{1}{{\sqrt 2 }}\)
Công suất tiêu thụ của mạch là:
\(P = {I^2}R = \frac{1}{2}.100 = 50W\)
Cho đoạn mạch nối tiếp theo thứ tự gồm điện trở R, tụ điện có điện dung C và cuộn dây có độ tự cảm L, điện trở r. Biết \(L = C{R^2} = C{r^2}.\) Đặt vào đoạn mạch điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t(V)\) thì điện áp hiệu dụng của đoạn mạch RC gấp \(\sqrt 3 \) lần điện áp hiệu dụng hai đầu cuộn dây. Hệ số công suất của đoạn mạch là
-
A
0,866
-
B
0,657
-
C
0,785
-
D
0,5
Đáp án của giáo viên lời giải hay : A
Vận dụng công thức tính hệ số công suất: \({\rm{cos}}\varphi = \frac{R}{Z}\)
Ta có:
\(\begin{array}{l}L = {R^2}C = {r^2}C\\ = > {Z_L}.Z_C^{} = {R^2} = {r^2}\end{array}\)
Điện áp hiệu dụng của đoạn mạch RC gấp \(\sqrt 3 \) lần điện áp hiệu dụng hai đầu cuộn dây
\(\begin{array}{l}I.\sqrt {{R^2} + Z_C^2} = \sqrt 3 .I.\sqrt {{r^2} + Z{{_L^2}^{}}} < = > {R^2} + Z_C^2 = 3({r^2} + Z_L^2)\\ < = > {Z_L}.{Z_C} + Z_C^2 = 3.{Z_L}.{Z_C} + 3Z_L^2\\ < = > {Z_C}(Z_L^{} + {Z_C}) = 3{Z_L}({Z_L} + {Z_C})\\ = > {Z_C} = 3{Z_L} = > {R^2} = 3Z_L^2 = > R = Z{}_L\sqrt 3 \end{array}\)
=> Hệ số công suất của đoạn mạch là
\(\cos \varphi = \frac{{R + r}}{{\sqrt {{{(R + r)}^2} + {{({Z_L} - Zc)}^2}} }} = \frac{{2R}}{{\sqrt {4{R^2} + 4Z_L^2} }} = \frac{{2\sqrt 3 {Z_L}}}{{\sqrt {4.3.Z_L^2 + 4Z_L^2} }} = \frac{{\sqrt 3 }}{2}\)
Đặt điện áp xoay chiều \(u = {U_0}cos\omega t\)(\(\omega \) và U0 là các hằng số) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(R_1\) và cuộn cảm thuần \(L\) thì dòng điện qua mạch có cường độ hiệu dụng \(I\) và trễ pha \(\dfrac{\pi }{6}\) so với điện áp hai đầu đoạn mạch. Nếu đặt điện áp trên vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(R_2\) và tụ điện \(C\) thì dòng điện qua mạch cũng có cường độ hiệu dụng \(I\) nhưng sớm pha \(\dfrac{\pi }{4}\) so với điện áp hai đầu đoạn mạch. Nếu đặt điện áp trên vào hai đầu đoạn mạch gồm \(R_1\), \(R_2\), \(L\) và \(C\) mắc nối tiếp thì hệ số công suất của mạch có giá trị gần nhất với giá trị nào sau đây ?
-
A
\(0,899\).
-
B
\(0,991\).
-
C
\(0,905\).
-
D
\(0,893\).
Đáp án của giáo viên lời giải hay : B
Áp dụng công thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Sử dụng phương pháp chuẩn hóa số liệu
+ Mạch R1,L: \(\tan {\varphi _1} = \dfrac{{{Z_L}}}{{{R_1}}} = \tan \dfrac{\pi }{6} = \dfrac{1}{{\sqrt 3 }} \to {R_1} = {Z_L}\sqrt 3 \to {Z_1} = \dfrac{{2{R_1}}}{{\sqrt 3 }}(*).\)
+ Mạch R2,C: \(\tan {\varphi _2} = \dfrac{{ - {Z_C}}}{{{R_2}}} = \tan \dfrac{{ - \pi }}{4} = - 1 \to {R_2} = {Z_C} \to {Z_2} = {R_2}\sqrt 2 (**).\)
+ Mạch R1,L và mạch R2, C: Cùng U, có cùng I à \({Z_1}\)= \({Z_2}\), từ (*) và (**) à \({R_1} = {R_2}\sqrt {\dfrac{3}{2}} \).
+ Chuẩn hóa: \({R_2} = 1 \to {Z_C} = 1 \to {R_1} = \sqrt {\dfrac{3}{2}} \to {Z_L} = \dfrac{1}{{\sqrt 2 }}.\)
+ Mạch gồm R1, R2, L và C mắc nối tiếp thì hệ số công suất: \({\rm{cos}}\varphi = \dfrac{{{R_1} + {R_2}}}{{\sqrt {{{({R_1} + {R_2})}^2} + {{({Z_L} - {Z_C})}^2}} }} \approx \)\(0,991\)
Đoạn mạch điện xoay chiều không phân nhánh gồm cuộn dây có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C. Khi dòng điện có tần số góc \(\frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì hệ số công suất của đoạn mạch này.
-
A
phụ thuộc điện trở thuần của đoạn mạch.
-
B
bằng 0.
-
C
phụ thuộc tổng trở của đoạn mạch.
-
D
bằng 1
Đáp án của giáo viên lời giải hay : D
Hệ số công suất:
\(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Khi có cộng hưởng điện:
\({Z_L} = {Z_C} \Rightarrow \omega = \frac{1}{{\sqrt {LC} }}\)
Khi dòng điện có tần số góc \(\omega = \frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì trong mạch xảy ra cộng hưởng điện.
Hệ số công suất bằng:
\(\cos \varphi = \frac{R}{Z} = \frac{R}{R} = 1\)
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số 50 Hz vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung C đến giá trị \(\dfrac{1}{{40\pi }}\,\,mF\) hoặc \(\dfrac{1}{{20\pi }}\,\,mF\) thì công suất tiêu thụ trên đoạn mạch đều có giá trị bằng nhau. Giá trị của L bằng
-
A
\(\dfrac{1}{{2\pi }}\,\,H\)
-
B
\(\dfrac{3}{\pi }\,\,H\)
-
C
\(\dfrac{1}{{3\pi }}\,\,H\)
-
D
\(\dfrac{2}{\pi }\,\,H\)
Đáp án của giáo viên lời giải hay : B
Công suất của mạch điện xoay chiều: \(P = \dfrac{{{U^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Hai giá trị dung kháng của tụ điện là:
\(\left\{ \begin{array}{l}{Z_{{C_1}}} = \dfrac{1}{{2\pi f{C_1}}} = \dfrac{1}{{2\pi .50.\dfrac{{{{1.10}^{ - 3}}}}{{20\pi }}}} = 200\,\,\left( \Omega \right)\\{Z_{{C_2}}} = \dfrac{1}{{2\pi f{C_2}}} = \dfrac{1}{{2\pi .50.\dfrac{{{{1.10}^{ - 3}}}}{{40\pi }}}} = 400\,\,\left( \Omega \right)\end{array} \right.\)
Công suất trên mạch có giá trị bằng nhau, ta có:
\(\begin{array}{l}P = \dfrac{{{U^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_{{C_1}}}} \right)}^2}}} = \dfrac{{{U^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_{{C_2}}}} \right)}^2}}}\\ \Rightarrow \left| {{Z_L} - {Z_{{C_1}}}} \right| = \left| {{Z_L} - {Z_{{C_2}}}} \right| \Rightarrow \left| {{Z_L} - 400} \right| = \left| {{Z_L} - 200} \right| \Rightarrow {Z_L} = 300\,\,\left( \Omega \right)\end{array}\)
Mặt khác: \({Z_L} = 2\pi fL \Rightarrow 300 = 2.50\pi .L \Rightarrow L = \dfrac{3}{\pi }\,\,\left( H \right)\)
Mạch RLC nối tiếp có \(R = 25\,\,\Omega ;\,\,C = \dfrac{{{{10}^{ - 4}}}}{\pi }\,\,F\) và L là cuộn dây thuần cảm biến đổi được. Hiệu điện thế giữa hai đầu mạch là \(u = 200\sqrt 2 \cos \left( {100\pi t - \dfrac{\pi }{2}} \right)\,\,\left( V \right)\). Thay đổi L sao cho công suất mạch đạt cực đại. Giá trị của L khi đó là
-
A
\(L = \dfrac{1}{{2\pi }}\,\,H\)
-
B
\(L = \dfrac{1}{\pi }\,\,H\)
-
C
\(L = \dfrac{2}{\pi }\,\,H\)
-
D
\(L = \dfrac{4}{\pi }\,\,H\)
Đáp án của giáo viên lời giải hay : B
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\)
Cảm kháng của cuộn dây: \({Z_L} = \omega L\)
L thay đổi, công suất trong mạch đạt cực đại khi xảy ra cộng hưởng: \({Z_L} = {Z_C}\)
Dung kháng của tụ điện là: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\,\,\left( \Omega \right)\)
Công suất trong mạch đạt cực đại khi:
\({Z_L} = {Z_C} = 100\,\,\left( \Omega \right) \Rightarrow \omega L = 100 \Rightarrow 100\pi L = 100 \Rightarrow L = \dfrac{1}{\pi }\,\,\left( H \right)\)
Đoạn mạch AB gồm hai đoạn AD và DB ghép nối tiếp. Điện áp tức thời trên các đoạn mạch và dòng điện qua chúng lần lượt có biểu thức \({u_{AD}} = 100\sqrt 2 \cos \left( {100\pi t + \dfrac{\pi }{2}} \right)\,\,\left( V \right)\); \({u_{DB}} = 100\sqrt 6 \cos \left( {100\pi t + \dfrac{{2\pi }}{3}} \right)\,\,\left( V \right)\); \(i = \sqrt 2 \cos \left( {100\pi t + \dfrac{\pi }{2}} \right)\,\,\left( A \right)\). Công suất tiêu thụ của đoạn mạch AB là
-
A
100 W
-
B
242 W
-
C
186,6 W
-
D
250 W
Đáp án của giáo viên lời giải hay : D
Công thức cộng hiệu điện thế: \({u_{AB}} = {u_{AD}} + {u_{DB}}\)
Sử dụng máy tính bỏ túi để tìm dao động tổng hợp
Độ lệch pha giữa hiệu điện thế và cường độ dòng điện: \(\Delta \varphi = {\varphi _u} - {\varphi _i}\)
Công suất tiêu thụ của đoạn mạch: \(P = UI\cos \Delta \varphi \)
Ta có hiệu điện thế giữa hai đầu đoạn mạch là:
\(\begin{array}{l}{u_{AB}} = {u_{AD}} + {u_{DB}} = 100\sqrt 2 \angle \dfrac{\pi }{2} + 100\sqrt 6 \angle \dfrac{{2\pi }}{3} = 100\sqrt {14} \angle 1,9\\ \Rightarrow \left\{ \begin{array}{l}{U_{0AB}} = 100\sqrt {14} \,\,\left( V \right) \Rightarrow {U_{AB}} = \dfrac{{{U_{0AB}}}}{{\sqrt 2 }} = \dfrac{{100\sqrt {14} }}{{\sqrt 2 }} = 100\sqrt 7 \,\,\left( V \right)\\{\varphi _u} = 1,9\,\,\left( {rad} \right) \Rightarrow \Delta \varphi = {\varphi _u} - {\varphi _i} = 1,9 - \dfrac{\pi }{2} = 0,33\,\,\left( {rad} \right) = 18,{86^0}\end{array} \right.\end{array}\)
Công suất tiêu thụ của đoạn mạch là:
\(P = UI\cos \Delta \varphi = 100\sqrt 7 .1.cos18,86 = 250\,\,\left( W \right)\)
Một quạt điện xoay chiều mắc nối tiếp với điện trở R rồi mắc hai đầu đoạn mạch này vào điện áp xoay chiều có giá trị hiệu dụng 380 V. Biết quạt điện này có giá trị định mức 220V – 80 W và khi hoạt động đúng công suất định mức thì độ lệch pha giữa điện áp ở hai đầu quạt và cường độ dòng điện chạy qua nó là φ với cosφ = 0,8. Để quạt điện chạy gần đúng công suất định mức nhất thì R có giá trị
-
A
230,4Ω
-
B
360,7Ω
-
C
396,7Ω
-
D
180,4Ω
Đáp án của giáo viên lời giải hay : C
Ta coi đoạn mạch gồm R nối tiếp quạt là điện trở R nối tiếp với đọan mạch RLC nối tiếp.
Áp dụng công thức tính công suất của quạt \(P = U.I.\cos \varphi \) ta tính được cường độ dòng điện I
Vẽ giản đồ vecto của đoạn mạch.
Từ đó ta tìm được UR từ giản đồ vecto:
\(U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \)
Xác định được điện trở R:
\(R = \frac{{{U_R}}}{I}\)
Áp dụng công thức tính công suất của quạt:
\(P = U.I.\cos \varphi \Rightarrow I = \frac{P}{{U.\cos \varphi }} = \frac{{80}}{{220.0,8}} = \frac{5}{{11}}A\)
Mạch điện có giản đồ vecto:
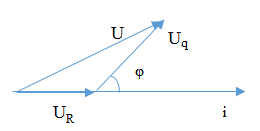
Từ đó ta tìm được UR từ giản đồ vecto:
\(\begin{gathered}
U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \hfill \\
\Leftrightarrow {380^2} = U_R^2 + {220^2} - 2.{U_R}.220.( - \cos \varphi ) \Rightarrow {U_R} = 180V \hfill \\
\end{gathered} \)
Xác định được điện trở R:
\(R = \frac{{{U_R}}}{I} = \frac{{180}}{{\frac{5}{{11}}}} = {396_{}}\Omega \)
Đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R1 = 40Ω mắc nối tiếp với tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 3}}}}{{4\pi }}F\), đoạn mạch MB gồm điện trở thuần R2 mắc nối tiếp với cuộn cảm thuần. Đặt vào A, B điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi thì điện áp tức thời ở hai đầu đoạn mạch AM và MB lần lượt là \({u_{AM}} = 50\sqrt 2 .\cos \left( {100\pi t - \dfrac{{7\pi }}{{12}}} \right)\,\left( V \right)\)và \({u_{MB}} = 150.\cos 100\pi t\,\,\left( V \right)\). Hệ số công suất của đoạn mạch AB là:
-
A
0,86
-
B
0,84
-
C
0,95
-
D
0,71
Đáp án của giáo viên lời giải hay : B
Độ lệch pha của uAM và uMB so với i được xác định bởi: \(\left\{ \begin{array}{l}\tan {\varphi _{AM}} = - \dfrac{{{Z_C}}}{{{R_1}}}\\\tan {\varphi _{MB}} = \dfrac{{{Z_L}}}{{{R_2}}}\end{array} \right.\)
Áp dụng các công thức tính tổng trở, độ lệch pha của u và i và biến đổi toán học tính ra R2; ZL
Hệ số công suất của đoạn mạch AB: \(\cos \varphi = \dfrac{{{R_1} + {R_2}}}{{\sqrt {{{\left( {{R_1} + {R_2}} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Đoạn mạch AM có:
\(\left\{ \begin{array}{l}{R_1} = 40\Omega \\{Z_C} = \dfrac{1}{{\omega C}} = 40\Omega \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{Z_{AM}} = 40\sqrt 2 \Omega \\\tan {\varphi _{AM}} = - \dfrac{{{Z_C}}}{{{R_1}}} = - 1 \Rightarrow {\varphi _{uAM}} - {\varphi _i} = - \dfrac{\pi }{4}\end{array} \right.\)
Dòng điện hiệu dụng chạy qua mạch:
\(I = \dfrac{{{U_{AM}}}}{{{Z_{AM}}}} = \dfrac{{50}}{{40\sqrt 2 }} = \dfrac{{5\sqrt 2 }}{8}A\)
Từ hai biểu thức của điện áp tức thời ở hai đầu đoạn mạch AM và MB ta có:
\({\varphi _{uMB}} - {\varphi _{uAM}} = \dfrac{{7\pi }}{{12}} \Rightarrow {\varphi _{uAM}} = {\varphi _{uMB}} - \dfrac{{7\pi }}{{12}}\)
Mà: \({\varphi _{uAM}} - {\varphi _i} = - \dfrac{\pi }{4} \Rightarrow {\varphi _{uMB}} - \dfrac{{7\pi }}{{12}} - {\varphi _i} = - \dfrac{\pi }{4} \Rightarrow {\varphi _{uMB}} - {\varphi _i} = \dfrac{\pi }{3}\)
\( \Rightarrow \tan {\varphi _{MB}} = \tan \dfrac{\pi }{3} = \dfrac{{{Z_L}}}{{{R_2}}} \Rightarrow {Z_L} = \sqrt 3 .{R_2}\,\,\,\left( 1 \right)\)
Lại có: \({Z_{MB}} = \dfrac{{{U_{MB}}}}{I} = \dfrac{{75\sqrt 2 }}{{\dfrac{{5\sqrt 2 }}{8}}} = 120 \Rightarrow \sqrt {R_2^2 + Z_L^2} = 120\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra: \(\left\{ \begin{array}{l}{R_2} = 60\Omega \\{Z_L} = 60\sqrt 3 \Omega \end{array} \right.\)
Hệ số công suất của đoạn mạch:
\(\begin{array}{l}\cos \varphi = \dfrac{{{R_1} + {R_2}}}{{\sqrt {{{\left( {{R_1} + {R_2}} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ \Rightarrow \cos \varphi = \dfrac{{40 + 60}}{{\sqrt {{{\left( {40 + 60} \right)}^2} + {{\left( {60\sqrt 3 - 40} \right)}^2}} }} = 0,84\end{array}\)
Đặt điện áp \(u = 6\sqrt 2 \cos \left( {\omega t} \right)\,\,V\) (\(\omega \) không đổi) vào hai đầu đoạn mạch gồm cuộn dây mắc nối tiếp với tụ điện. Điện áp hiệu dụng hai đầu cuộn dây là \(10\;{\rm{V}}\) và sớm pha hơn điện áp hai đầu mạch là \(1,56{\rm{rad}}.\)Hệ số công suất của mạch là
-
A
\(0,40.\)
-
B
\(0,52\).
-
C
\(0,60.\)
-
D
\(0,86.\)
Đáp án của giáo viên lời giải hay : D
Vì độ lệch pha giữa \({u_d}\) và \(u\) là 1,56rad nên cuộn dây có điện trở thuần.
Sử dụng giản đồ vecto.
Ta có: \(\left( {{u_d},u} \right) = 1,56rad = \frac{\pi }{2};U = 6V;{U_d} = 10V\)
Vì điện áp hai đầu cuộn dây lệch pha với điện áp hai đầu đoạn mạch góc 1,56rad nên cuộn dây có điện trở thuần.
Ta có giản đồ vecto:
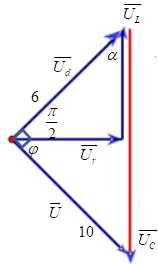
Từ giản đồ vecto ta có: \(\tan \alpha = \frac{6}{{10}} = 0,6\)
\( \Rightarrow \alpha = shif\tan 0,6 = 0,54042\) \( \Rightarrow \cos \alpha = 0,86\)
Mà \(\alpha = \varphi \Rightarrow \cos \varphi = 0,86\)
Đặt điện áp \(u = 220\sqrt 2 \cos (100\pi t)\left( V \right)\) vào hai đầu đoạn mạch \(AB\) gồm ba phần tử điện trở thuần \(R,\) cuộn cảm thuần có độ tự cảm \(L\) và tụ điện có điện dung \(C\) ghép nối tiếp. Biết \(R = 100\Omega ,L = \dfrac{{\sqrt 3 }}{\pi }H\). Khi thay đổi điện dung \(C\) của tụ điện thì cường dòng điện sớm pha hơn \(u\) một góc \(\dfrac{\pi }{3}rad\). Công suất tiêu thụ của đoạn mạch \(AB\) là
-
A
\(242\sqrt 2 W\)
-
B
\(242W\)
-
C
\(121W\)
-
D
\(121\sqrt 2 W\)
Đáp án của giáo viên lời giải hay : C
Công suất tiêu thụ: \(P = UI.cos\varphi = \dfrac{{{U^2}}}{R}.co{s^2}\varphi \)
Công suất tiêu thụ của đoạn mạch \(AB\) là:
\(P = \dfrac{{{U^2}}}{R}.co{s^2}\varphi = \dfrac{{{{220}^2}}}{{100}}.{\left( {\cos \dfrac{\pi }{3}} \right)^2} = 121W\)
Điện năng truyền tải đi xa thường bị hao phí chủ yếu do tỏa nhiệt trên đường dây. Gọi R là điện trở đường dây, P là công suất điện được truyền đi, U là điện áp tại nơi phát, \(co{\rm{s}}\varphi \) là hệ số công suất của mạch điện thì công suất hao phí trên đường dây là
-
A
\({P_{hp}} = R.\frac{{{{\left( {Uco{\rm{s}}\varphi } \right)}^2}}}{{{P^2}}}\)
-
B
\({P_{hp}} = R.\frac{{{U^2}}}{{{{\left( {P.co{\rm{s}}\varphi } \right)}^2}}}\)
-
C
\({P_{hp}} = {R^2}\frac{P}{{{{\left( {Uco{\rm{s}}\varphi } \right)}^2}}}\)
-
D
\({P_{hp}} = R.\frac{{{P^2}}}{{{{\left( {Uco{\rm{s}}\varphi } \right)}^2}}}\)
Đáp án của giáo viên lời giải hay : D
Công thức tính công suất hao phí: \({P_{hp}} = \frac{{{P^2}}}{{{U^2}co{{\rm{s}}^2}\varphi }}R\)
Công suất hao phí trên đường dây: \({P_{hp}} = \frac{{{P^2}}}{{{U^2}co{{\rm{s}}^2}\varphi }}R\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Mắc một biến trở R vào hai cực của một nguồn điện một chiều có suất điện động \(\xi = 6V\) và điện trở trong \(r\). Đồ thị biểu diễn hiệu suất H của nguồn điện theo biến trở R như hình vẽ bên. Công suất tiêu thụ cực đại trên R có giá trị bằng
-
A
2,5W.
-
B
4,5W.
-
C
9W.
-
D
18W.
Đáp án của giáo viên lời giải hay : C
+ Đọc đồ thị
+ Sử dụng biểu thức tính hiệu suất: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)
+ Sử dụng biểu thức tính công suất: \(P = {I^2}R\)
+ Sử dụng BĐT Cosi
Ta có: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)
Từ đồ thị ta có tại \(R = 3\Omega \) thì \(H = 0,75\)
\( \Leftrightarrow \frac{R}{{R + r}} = 0,75 \Leftrightarrow \frac{3}{{3 + r}} = 0,75 \Rightarrow r = 1\Omega \)
Công suất tiêu thụ trên R:
\({P_R} = {I^2}R = \frac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R = \frac{{{E^2}}}{{{{\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)}^2}}}\)
\( \Rightarrow {P_{Rma{\rm{x}}}}\) khi \({\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)^2}_{\min }\)
Áp dụng BĐT Cosi ta có: \(\sqrt R + \frac{r}{{\sqrt R }} \ge 2\sqrt r = 2\)
\( \Rightarrow \sqrt R + \frac{r}{{\sqrt R }} = 2\sqrt r = 2\) khi \(\sqrt R = \frac{r}{{\sqrt R }}\)hay \(R = r\)
\( \Rightarrow {P_{R\max }} = \frac{{{E^2}}}{{4{\rm{R}}}} = \frac{{{E^2}}}{{4{\rm{r}}}} = \frac{{{6^2}}}{4} = 9W\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đâu đoạn mạch AB mắc nối tiếp gồm điện trở R không đổi và cuộn cảm thuần có độ tự cảm L thay đổi được. Gọi \(\varphi \) là độ lệch pha của điện áp hai đầu đoạn mạch và cường độ dòng điện trong đoạn mạch. Hình vẽ bên là đồ thị của công suất mà mạch tiêu thụ theo giá trị của \(\varphi \). Giá trị \({\varphi _1}\) gần giá trị nào nhất sau đây?
-
A
0,42 rad.
-
B
0,48 rad.
-
C
0,52 rad.
-
D
0,32 rad.
Đáp án của giáo viên lời giải hay : C
+ Đọc đồ thị
+ Sử dụng biểu thức tính công suất: \(P = UIco{\rm{s}}\varphi \)
+ Sử dụng biểu thức tính: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Từ đồ thị ta có:
Khi \(\varphi = 0 \to {P_{ma{\rm{x}}}} = {P_0} = \frac{{{U^2}}}{R}\,\,\,\,\left( 1 \right)\)
Khi \(\varphi = {\varphi _1} \to P = \frac{3}{4}{P_0} = UI\cos \varphi = \frac{{{U^2}}}{{{Z^2}}}R\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta suy ra: \(\frac{3}{4}\frac{{{U^2}}}{R} = \frac{{{U^2}}}{{{Z^2}}}R\)
\( \Rightarrow 3{{\rm{Z}}^2} = 4{{\rm{R}}^2} \Leftrightarrow 3\left( {{R^2} + Z_L^2} \right) = 4{{\rm{R}}^2} \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\)
Lại có: \(\tan {\varphi _1} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} \Rightarrow {\varphi _1} = \frac{\pi }{6}\) rad
Một máy pha cà phê có công suất 1200 W được mắc vào một nguồn điện có điện áp hiệu dụng là 220 V. Giả sử máy đang được sử dụng đúng định mức công suất và coi hệ số công suất của mạch điện bằng 1. Khi này, dòng điện trong mạch có cường độ hiệu dụng gần nhất với giá trị nào sau đây?
-
A
7A
-
B
6A
-
C
5A
-
D
4A
Đáp án của giáo viên lời giải hay : C
Sử dụng công thức: \(P = UI\cos \varphi \)
Cường độ dòng điện hiệu dụng trong mạch là:
\(I = \dfrac{P}{{U\cos \varphi }} = \dfrac{{1200}}{{220.1}} = \dfrac{{60}}{{11}} \approx 5,45\left( A \right)\)
Cho hai đoạn mạch X và Y là các đoạn mạch điện xoay chiều không phân nhánh. Nếu mắc đoạn mạch X vào hiệu điện thế xoay chiều \(u = {U_0}\cos \left( {\omega t} \right)\) thì cường độ dòng điện qua mạch lệch pha \(\frac{\pi }{6}\) so với hiệu điện thế giữa hai đầu đoạn mạch. Công suất tiêu thụ trên X khi đó là \({P_1} = 250\sqrt 3 W\). Nếu mắc nối tiếp hai đoạn mạch X và Y rồi nối vào hiệu điện thế xoay chiều như trường hợp trước thì điện áp giữa hai đầu của đoạn mạch X và đoạn mạch Y vuông pha với nhau. Công suất tiêu thụ trên X lúc này là \({P_2} = 90\sqrt 3 W\). Công suất tiêu thụ trên Y bằng bao nhiêu W?
-
A
\(120W\)
-
B
\(90W\)
-
C
\(150W\)
-
D
\(100W\)
Đáp án của giáo viên lời giải hay : A
Độ lệch pha giữa điện áp và cường độ dòng điện: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Cường độ dòng điện: \(I = \dfrac{U}{{\sqrt {{{\left( {{Z_L} - {Z_C}} \right)}^2} + {R^2}} }}\)
Công suất tiêu thụ của đoạn mạch: \(P = {I^2}R\)
Khi mắc điện áp u vào hai đầu đoạn mạch X, độ lệch pha giữa điện áp và cường độ dòng điện là:
\(\tan \varphi = \dfrac{{{Z_{L1}} - {Z_{C1}}}}{{{R_1}}} = \tan \dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{3} \Rightarrow {Z_{L1}} - {Z_{C1}} = \dfrac{{\sqrt 3 }}{3}{R_1}\)
Chuẩn hóa \({R_1} = 1 \Rightarrow {Z_{L1}} - {Z_{C1}} = \dfrac{{\sqrt 3 }}{3}\)
Công suất tiêu thụ trên đoạn mạch X là:
\(\begin{array}{l}P = \dfrac{{{U_{R1}}^2}}{{{R_1}}} = \dfrac{{{{\left( {U.cos\varphi } \right)}^2}}}{{{R_1}}} \Rightarrow \frac{{{U^2}.{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}^2}}}{{{R_1}}} = 250\sqrt 3 \\ \Rightarrow {U^2} = \dfrac{{1000\sqrt 3 }}{3}{R_1} = \dfrac{{1000\sqrt 3 }}{3}\end{array}\)
Khi mắc điệu áp u vào hai đầu đoạn mạch X, Y mắc nối tiếp
Điện áp giữa hai đầu đoạn mạch X và Y vuông pha, ta có:
\(\begin{array}{l}\tan {\varphi _1}.\tan {\varphi _2} = - 1 \Rightarrow \dfrac{{{Z_{L1}} - {Z_{C1}}}}{{{R_1}}}.\dfrac{{{Z_{L2}} - {Z_{C2}}}}{{{R_2}}} = - 1\\ \Rightarrow \frac{{\sqrt 3 }}{3}.\dfrac{{{Z_{L2}} - {Z_{C2}}}}{{{R_2}}} = - 1 \Rightarrow {Z_{L2}} - {Z_{C2}} = - \sqrt 3 {R_2}\end{array}\)
Cường độ dòng điện trong mạch là:
\(I = \dfrac{U}{{\sqrt {{{\left[ {\left( {{Z_{L1}} - {Z_{C1}}} \right) + \left( {{Z_{L2}} - {Z_{C2}}} \right)} \right]}^2} + {{\left( {{R_1} + {R_2}} \right)}^2}} }}\)
\( \Rightarrow I = \dfrac{U}{{\sqrt {{{\left( {\dfrac{{\sqrt 3 }}{3} - \sqrt 3 {R_2}} \right)}^2} + {{\left( {1 + {R_2}} \right)}^2}} }} = \dfrac{U}{{\sqrt {\dfrac{4}{3} + 4{R_2}^2} }}\)
Công suất tiêu thụ của đoạn mạch X là:
\(\begin{array}{l}{P_1} = {I^2}{R_1} = \dfrac{{{U^2}{R_1}}}{{\dfrac{4}{3} + 4{R_2}^2}} = 90\sqrt 3 \\ \Rightarrow \dfrac{{\dfrac{{1000\sqrt 3 }}{3}}}{{\dfrac{4}{3} + 4{R_2}^2}} = 90\sqrt 3 \Rightarrow {R_2}^2 = \dfrac{{16}}{{27}} \Rightarrow {R_2} = \dfrac{4}{{3\sqrt 3 }}\end{array}\)
Công suất tiêu thụ trên đoạn mạch Y là:
\({P_2} = {I^2}{R_2} = \dfrac{{{U^2}{R_2}}}{{\dfrac{4}{3} + 4{R_2}^2}} = \dfrac{{\dfrac{{1000\sqrt 3 }}{3}.\dfrac{4}{{3\sqrt 3 }}}}{{\dfrac{4}{3} + 4.\dfrac{{16}}{{27}}}} = 120\,\,\left( {\rm{W}} \right)\)
Cho đoạn mạch AB gồm đoạn AM nối tiếp với MB. Biết đoạn AM gồm điện trở R nối tiếp với tụ điện có điện dung C và MB chứa cuộn dây có độ tự cảm L và có điện trở r. Đặt vào AB một điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\,\,\left( V \right)\). Biết \(R = r = \sqrt {\dfrac{L}{C}} \), điện áp hiệu dụng \({U_{MB}} = \sqrt 3 {U_{AM}}\). Hệ số công suất của đoạn mạch gần với giá trị nào nhất sau đây?
-
A
0,887.
-
B
0,975.
-
C
0,755.
-
D
0,866.
Đáp án của giáo viên lời giải hay : D
Tổng trở: \(Z = \sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Sử dụng phương pháp chuẩn hóa số liệu
Hẹ số công suất: \(\cos \varphi = \dfrac{{R + r}}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Ta có: \(R = r = \sqrt {\dfrac{L}{C}} = \sqrt {{Z_L}.{Z_C}} \)
Theo đề bài có điện áp hiệu dụng:
\(\begin{array}{l}{U_{MB}} = \sqrt 3 {U_{AM}} \Rightarrow {U_{cd}} = \sqrt 3 {U_{RC}} \Rightarrow {Z_{cd}}^2 = 3{Z_{RC}}^2\\ \Rightarrow {r^2} + {Z_L}^2 = 3\left( {{R^2} + {Z_C}^2} \right) \Rightarrow {R^2} + {Z_L}^2 = 3{R^2} + 3{Z_C}^2\\ \Rightarrow {Z_L}^2 - 2{R^2} - 3{Z_C}^2 = 0 \Rightarrow {Z_L}^2 - 2{Z_L}{Z_C} - 3{Z_C}^2 = 0\\ \Rightarrow {Z_L} = 3{Z_C}\end{array}\)
Chuẩn hóa \({Z_C} = 1 \Rightarrow {Z_L} = 3 \Rightarrow R = r = \sqrt 3 \)
Hệ số công suất của mạch là:
\(\cos \varphi = \dfrac{{R + r}}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{2\sqrt 3 }}{{\sqrt {{{\left( {2\sqrt 3 } \right)}^2} + {2^2}} }} \approx 0,866\)
Một nhà vườn trồng hoa phục vụ dịp tết. Do thời tiết lạnh kéo dài, để hoa nở đúng tết phải dùng các bóng đèn sợi đốt loại \(200V - 220W\)để thắp sáng và sưởi ấm vườn hoa vào ban đêm. Biết điện năng được truyền từ trạm điện đến nhà vườn bằng đường tải một pha có điện trở \(50\Omega \), điện áp hiệu dụng tại trạm là 1500V. Ở nhà vườn, người ta dùng máy hạ áp lý tưởng. Coi rằng hao phí điện năng chỉ xảy ra trên đường dây tải điện và hệ số công suất của mạch luôn bằng 1. Để các đèn sáng bình thường thì số bóng đèn tối đa mà nhà vườn có thể sử dụng cùng lúc là
-
A
\(50\)
-
B
\(66\)
-
C
\(56\)
-
D
\(60\)
Đáp án của giáo viên lời giải hay : A
+ Công suất hao phí: \(\Delta P = \dfrac{{{P^2}}}{{{U^2}co{s^2}\varphi }}R\)
+ Công suất có ích: \({P_{ci}} = P - \Delta P\)
Gọi P là công suất nơi phát, n là số bóng đèn nhà vườn sử dụng.
Tổng công suất các bóng đèn tiêu thụ:
\(P' = 220n = P - \Delta P\)
\(\begin{array}{l} \Rightarrow 220n = P - \dfrac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R = P - \dfrac{{{P^2}}}{{{{1500}^2}}}.50\\ \Rightarrow 50{P^2} - 22,{5.10^5}P + 49,{5.10^7}.n = 0\end{array}\)
Để phương trình có nghiệm thì:
\(\Delta \ge 0 \Leftrightarrow {b^2} - 4.a.c \ge 0\)
\( \Leftrightarrow {\left( {22,{{5.10}^5}} \right)^2} - 4.50.49,{5.10^7}n \ge 0\)
\( \Leftrightarrow n \le 51,136 \Rightarrow {n_{\max }} = 51\)
\( \Rightarrow \) Số bóng tối đa mà nhà vườn có thể sử dụng cùng lúc là 51 bóng.
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P1, P2 và P3. Biểu thức nào sau đây đúng?
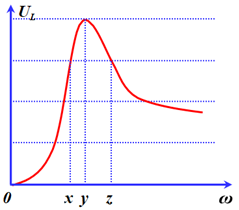
-
A
\(\dfrac{{{P_1} + {P_3}}}{8} = \dfrac{{{P_2}}}{9}\).
-
B
\(\dfrac{{{P_1} + {P_3}}}{9} = \dfrac{{{P_2}}}{8}\).
-
C
\(\dfrac{{{P_1} + {P_2}}}{{16}} = \dfrac{{{P_3}}}{9}\).
-
D
\(\dfrac{{{P_1} + {P_2}}}{9} = \dfrac{{{P_3}}}{{16}}\).
Đáp án của giáo viên lời giải hay : B
Sử dụng kĩ năng đọc đồ thị
Điện áp ULmax khi tần số có giá trị ω2
Hai tần số ω1, ω3 cho cùng giá trị điện áp \({U_L}:\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}} = \dfrac{2}{{{\omega _2}^2}}\)
Độ lệch pha giữa điện áp và cường độ dòng điện: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Điện áp hiệu dụng giữa hai đầu cuộn dây: \({U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Công suất tiêu thụ: \(P = \dfrac{{{U^2}{{\cos }^2}\varphi }}{R}\)
Điện áp hiệu dụng giữa hai đầu cuộn dây là:
\({U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_L}}}{R}.\dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_L}.cos\varphi }}{R}\)
Với tần số ω1 = x; ω2 = y và ω3 = z, ta có:
\(\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}} = \dfrac{2}{{{\omega _2}^2}}\)
Từ đồ thị ta thấy:
\(\begin{array}{l}{U_{L1}} = {U_{L3}} = \dfrac{3}{4}{U_{L2}} = \dfrac{3}{4}{U_{L\max }}\\ \Rightarrow \dfrac{{U.{Z_{L1}}\cos {\varphi _1}}}{R} = \dfrac{{U.{Z_{L3}}\cos {\varphi _3}}}{R} = \dfrac{3}{4}\dfrac{{U.{Z_{L2}}\cos {\varphi _2}}}{R}\\ \Rightarrow {\omega _1}^2{\cos ^2}{\varphi _1} = {\omega _3}^2{\cos ^2}{\varphi _3} = \dfrac{9}{{16}}{\omega _2}^2{\cos ^2}{\varphi _2}\\ \Rightarrow \left\{ \begin{array}{l}\dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}\dfrac{{{\omega ^2}}}{{{\omega _1}^2}}\\\dfrac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}\varphi }} = \dfrac{9}{{16}}\dfrac{{{\omega ^2}}}{{{\omega _2}^2}}\end{array} \right. \Rightarrow \dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \dfrac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}{\omega ^2}.\left( {\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}}} \right)\\ \Rightarrow \dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \dfrac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}{\omega _2}^2.\dfrac{2}{{{\omega _2}^2}} = \dfrac{9}{8}\,\,\left( 1 \right)\end{array}\)
Công suất tiêu thụ của mạch điện là:
\(P = \dfrac{{{U^2}{{\cos }^2}\varphi }}{R} \Rightarrow P \sim {\cos ^2}\varphi \)
Từ (1) ta có: \(\dfrac{{{P_1}}}{{{P_2}}} + \dfrac{{{P_3}}}{{{P_2}}} = \dfrac{9}{8} \Rightarrow \dfrac{{{P_1} + {P_3}}}{9} = \dfrac{{{P_2}}}{8}\)
Một đoạn mạch gồm điện trở thuần R, cuộn dây cảm thuần có độ tự cảm L, tụ điện có điện dung C thay đổi được mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 .\cos \left( {100\pi t} \right)V\). Khi \(C = {C_1}\) thì công suất tiêu thụ của mạch là \(P = 100W\) và cường độ dòng điện qua mạch có biểu thức \(i = {I_0}.\cos \left( {100\pi t + \dfrac{\pi }{3}} \right)A\). Khi \(C = {C_2}\), công suất tiêu thụ của mạch đạt cực đại. Giá trị cực đại đó là:
-
A
\(100W\)
-
B
\(400W\)
-
C
\(200W\)
-
D
\(150W\)
Đáp án của giáo viên lời giải hay : B
Công suất tiêu thụ :\(P = {I^2}.R = \dfrac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}\)
Độ lệch pha giữa u và i được xác định : \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Thay đổi C để P cực đại thì tức là xảy ra cộng hưởng, khi đó \({P_{\max }} = \dfrac{{{U^2}}}{R}\)
Khi C = C1 thì độ lệch pha giữa u và i được xác định:
\(\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_{{C_1}}}}}{R} \Rightarrow \tan \dfrac{{ - \pi }}{3} = \dfrac{{{Z_L} - {Z_C}_1}}{R} = - \sqrt 3 \\ \Rightarrow {Z_L} - {Z_{{C_1}}} = - \sqrt 3 .R\end{array}\)
Áp dụng công thức tính công suất:
\(\begin{array}{l}P = {I^2}.R = \dfrac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_{{C_1}}})}^2}}} \Rightarrow 100 = \dfrac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_{C1}})}^2}}}\\ \Rightarrow 100 = \dfrac{{{U^2}.R}}{{{R^2} + {{( - \sqrt 3 R)}^2}}} = \dfrac{{{U^2}}}{{4.R}}\end{array}\)
Thay đổi C để P cực đại thì tức là xảy ra cộng hưởng, khi đó:
\({P_{\max }} = \dfrac{{{U^2}}}{R} = 4.\dfrac{{{U^2}}}{{4.R}} = 4.100 = 400{\rm{W}}\)
