Đề bài
Lớp 11 ban AB
Câu 1(2 điểm). Giải các phương trình sau:
a) \(2\cos \left( {2x + \dfrac{\pi }{4}} \right) = \sqrt 3 \)
b) \(\sqrt 3 \sin x + \cos x = 2\)
Câu 2(1 điểm). Gieo một con súc sắc cân đối và đồng chất hai lần. Tính xác suất để số chấm xuất hiện trong hai lần gieo khác nhau.
Câu 3(1 điểm). Từ các chữ số 1;2;3;4;5;6 có thể lập được bao nhiêu số chẵn có 4 chữ số khác nhau?
Câu 4(1 điểm). Khai triển nhị thức \({\left( {1 - 3{\rm{x}}} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}\). Biết rằng \({a_0} + {a_1} + {a_2} = 376\), tính \({a_3}\).
Câu 5( 1 điểm). Cho dãy số \(\left( {{u_n}} \right)\) thỏa: \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = 2{u_n} + n\end{array} \right.\)
a) Chứng minh dãy số \({v_n} = {u_n} + n + 1\) là cấp số nhân.
b) Đặt \({\rm{S}} = {u_1} + {u_2} + ... + {u_n}\). Tính S theo n
Câu 6(1 điểm). Một số nguyên dương gọi là đối xứng nếu ta viết các chữ số theo thứ tự ngược lại thì được số bằng số ban đầu, ví dụ số 1221 là một số đối xứng. Chọn ngẫu nhiêu một số đói xứng có 4 chữ số , tính xác suất chọn được số chia hết cho 7.
Câu 7(1 điểm). Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi \(M,N,P\) lần lượt là các điểm trên cạnh \(CD,AD,SA\) thỏa mãn \(MD = 2MC,NA = 3ND,PA = 3PS\). Gọi G là trọng tâm tam giác SBC.
a) Tìm giao điểm K của đường thẳng BM và mặt phẳng (SAC).
b) Chứng minh rằng đường thẳng MG song song với mặt phẳng (SAD).
Lời giải chi tiết
Câu 1(VD).
Phương pháp:
a) \(\cos x = a\)
Với \(\left| a \right| > 1\), phương trình vô nghiệm.
Với \(\left| a \right| \le 1\), phương trình có 2 họ nghiệm:
\(\left[ \begin{array}{l}x = \arccos a + k2\pi \\x = - \arccos a + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
b) Giải phương trình \(a\sin x + b\cos x = c\)
Nếu \({c^2} > {a^2} + {b^2}\), phương trình vô nghiệm.
Nếu \({c^2} \le {a^2} + {b^2}\). Chia cả 2 vế phương trình cho \(\sqrt {{a^2} + {b^2}} \)
Đưa về dạng \(\cos x = a\) rồi giải tương tự câu a.
Giải:
a) \(2\cos \left( {2x + \dfrac{\pi }{4}} \right) = \sqrt 3 \)
\(\begin{array}{l} \Leftrightarrow \cos \left( {2x + \dfrac{\pi }{4}} \right) = \dfrac{{\sqrt 3 }}{2}\\ \Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{4} = \dfrac{\pi }{6} + k2\pi \\2x + \dfrac{\pi }{4} = - \dfrac{\pi }{6} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{24}} + k\pi \\x = \dfrac{{ - 5\pi }}{{24}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
b) \(\sqrt 3 \sin x + \cos x = 2\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin x + \dfrac{1}{2}\cos x = 1\\ \Leftrightarrow \sin \left( {x + \dfrac{\pi }{6}} \right) = 1\\ \Leftrightarrow x + \dfrac{\pi }{6} = \dfrac{\pi }{2} + k2\pi \\ \Leftrightarrow x = \dfrac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array}\)
Câu 2(VD).
Phương pháp:
Gọi A là biến cố thỏa mãn bài toán.
Tính \(P\left( {\overline A } \right)\)
Sử dụng phần bù \(P\left( A \right) = 1 - P\left( {\overline A } \right)\)
Giải:
Gọi A là biến cố “Số chấm trong 2 lần gieo khác nhau”
\(\overline A \) là biến cố “Số chấm trong 2 lần gieo giống nhau”
Xác suất 2 lần xuất hiện \(i\left( {1 \le i \le 6} \right)\) chấm là \(\dfrac{1}{6}.\dfrac{1}{6} = \dfrac{1}{{36}}\)
Xác xuất 2 lần gieo xuất hiện số chấm giống nhau là \(P\left( {\overline A } \right) = 6.\dfrac{1}{{36}} = \dfrac{1}{6}\)
Xác suất 2 lần gieo xuất hiện số chấm khác nhau: \(P\left( A \right) = 1 - P\left( {\overline A } \right) = \dfrac{5}{6}\)
Câu 3(VD).
Phương pháp:
Gọi số cần tìm là \(\overline {abcd} \).
Đếm số khả năng của d trước.
Đếm số khả năng của a,b,c.
Giải:
Gọi số cần tìm là \(\overline {abcd} \).
\(d \in \left\{ {2;4;6} \right\}\)
Với \(d = 2\), số cách sắp xếp thứ tự \(\overline {abc} \) là \(A_5^3\)
Với \(d = 4\), số cách sắp xếp thứ tự \(\overline {abc} \) là \(A_5^3\)
Với \(d = 6\), số cách sắp xếp thứ tự \(\overline {abc} \) là \(A_5^3\)
Vậy có \(3.A_5^3\) số.
Câu 4(1 điểm).
Phương pháp:
Khai triển nhị thức Niu-tơn rồi thay \(x = 1\), tìm \({a_0},{a_1},{a_2}\) theo n. Lập phương trình ẩn n ,tìm n.
Tìm hệ số \({a_3}\).
Giải:
\(\begin{array}{l}{\left( {1 - 3x} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{{\left( { - 3x} \right)}^k}} \\ = 1 + C_n^1\left( { - 3x} \right) + C_n^2{\left( { - 3x} \right)^2} + ... \\+ C_n^n.{\left( { - 3x} \right)^n}\\ \Rightarrow {a_0} = 1,{a_1} = - 3n,{a_2} \\= {\left( { - 3} \right)^2}.\dfrac{{n\left( {n - 1} \right)}}{2}\end{array}\)
\(\begin{array}{l} \Rightarrow 1 - 3n + \dfrac{9}{2}n\left( {n - 1} \right) = 376\\ \Leftrightarrow \left[ \begin{array}{l}n = 10\\n = - \dfrac{{25}}{3}\end{array} \right. \Leftrightarrow n = 10\end{array}\)
Số hạng chứa \({x^3}\) là \(C_{10}^3.{\left( { - 3x} \right)^3} = - 27C_{10}^3.{x^3}\)
Vậy \({a_3} = - 27.C_{10}^3 = - 3240\)
Câu 5( VD).
Phương pháp:
a) Biểu diễn \({v_n},{v_{n + 1}}\) theo \({u_n}\).
Nếu \(\exists q:{v_{n + 1}} = q{v_n}\forall n\) thì \(\left( {{v_n}} \right)\) là cấp số nhân.
b) Tính tổng \({V_n} = {v_1} + {v_2} + ... + {v_n}\) theo \({{\rm{S}}_n}\) và \(n\).
Tính \({V_n}\) theo công thức tổng cấp số nhân: \({V_n} = \dfrac{{{v_1}\left( {{q^n} - 1} \right)}}{{q - 1}}\)
Giải:
a) Ta có:
\(\begin{array}{l}{v_n} = {u_n} + n + 1\\ \Rightarrow {v_{n + 1}} = {u_{n + 1}} + n + 1 + 1\\ = \left( {2{u_n} + n} \right) + n + 2\\ = 2\left( {{u_n} + n + 1} \right) = 2{v_n}\forall n \in \mathbb{N}*\end{array}\)
Suy ra \(\left( {{v_n}} \right)\) là cấp số nhân công bội 2.
b) Ta có \({v_1} = 1 + 1 + 1 = 3\)
Xét tổng \({V_n} = {v_1} + {v_2} + ... + {v_n}\)\( = \dfrac{{{v_1}\left( {{q^n} - 1} \right)}}{{q - 1}} = \dfrac{{3.\left( {{2^n} - 1} \right)}}{{2 - 1}} \)\(= 3.\left( {{2^n} - 1} \right)\)
Ta có \({v_n} = {u_n} + n + 1\)
\(\begin{array}{l}{v_{n - 1}} = {u_{n - 1}} + n - 1 + 1\\{v_{n - 2}} = {u_{n - 2}} + n - 2 + 1\\....\\{v_1} = {u_1} + 1 + 1\end{array}\)
\(\begin{array}{l} \Rightarrow {V_n} = {S_n} + \left[ {n + \left( {n - 1} \right)+ \left( {n - 2} \right) + ... + 1} \right]\\ + n.1\\ = {S_n} + \dfrac{{n\left( {n + 1} \right)}}{2} + n\\ = {S_n} + \dfrac{{{n^2} + 3n}}{2}\\ \Rightarrow {S_n} = {V_n} - \dfrac{{{n^2} + 3n}}{2}\\ = 3.\left( {{2^n} - 1} \right) - \dfrac{{{n^2} + 3n}}{2}\end{array}\)
Câu 6(VD).
Phương pháp:
Gọi số đối xứng có 4 chữ số là \(\overline {abba} \)
Gọi A là biến cố “\(\overline {abba} \) chia hết cho 7”
Sử dụng công thức: \(\overline {abba} = a.1000 + b.100 + b.10 + a\).
Tách thành cách dạng \(7k + m\).
\(\overline {abba} \) chia hết cho 7\( \Leftrightarrow m\) chia hết cho 7.
Giải:
Gọi số đối xứng có 4 chữ số là \(\overline {abba} \)
Gọi A là biến cố “\(\overline {abba} \) chia hết cho 7”
Ta có \(n\left( \Omega \right) = 9.10 = 90\) (Do a có 9 cách chọn, b có 10 cách chọn).
Đếm số khả năng của A:
Ta có \(\overline {abba} = 1001.{\rm{a + 110}}{\rm{.b}}\)
\({\rm{ = }}\left( {1001.{\rm{a + 105}}{\rm{.b}}} \right) + 5b\)
Do \(1001 \vdots 7\) và \(105 \vdots 7\) nên để \(\overline {abba} \vdots 7\) thì \(5b \vdots 7\)
\( \Rightarrow b \in \left\{ {0;7} \right\}\) Có 2 cách chọn.
\(a \in \left\{ {1;2;3;...;9} \right\}\) có 9 cách chọn.
\( \Rightarrow n\left( A \right) = 2.9 = 18\)
\( \Rightarrow P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{1}{5}\).
Câu 7(VD).
Phương pháp:
a) Tìm đường thẳng trong (SAC) và cắt BM. Giao của đường thẳng đó và BM là K.
b) Nếu 2 đường thẳng cắt nhau trong (NPK) cùng song song với (SCD) thì (NPK) song song mặt phẳng (SCD).
c) Tìm hoặc dựng một mặt phẳng chứa MG và song song với (SAD). Khi đó MG song song với mặt phẳng (SAD).
Giải:
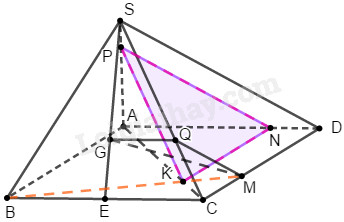
a) Xét (ABCD), ta có M thuộc CD và MD=2MC. Suy ra BM cắt AC. Mà \(AC \subset \left( {SAC} \right)\). Suy ra giao điểm của BM và AC là giao điểm của BM và (SAC). Vậy \(\left\{ K \right\} = AC \cap BM\).
b) Xét tam giác SAD, có \(NA = 3ND,PA = 3PS\), suy ra \(NP\)//\(SD\)
\( \Rightarrow NP\)//\(\left( {SCD} \right)\)(1).
Trong (ABCD) có CM//AB và \(CD = 3MC\) do \(MD = 2MC\) và \(CD = MD + MC\).
\( \Rightarrow AK = 3KC\)\( \Rightarrow KN\)//\(CD\)\( \Rightarrow KN\)//\(\left( {SCD} \right)\)(2)
Có \(NP,KN \subset \left( {NPK} \right)\) và \(NP \cap KN = \left\{ N \right\}\)(3)
Từ (1), (2) và (3) suy ra (NPK) song song mặt phẳng (SCD).
c) Qua M kẻ đường thẳng MQ \(\left( {Q \in SC} \right)\) song song với SD.
\( \Rightarrow MQ\)//\(\left( {SAD} \right)\) (4)
và \(SQ = 2QC\).
Gọi E là trung điểm của BC. Khi đó \(SG=2GE\).
\( \Rightarrow QG\)//\(EC\).
Mà EC//AD. Suy ra, \(QG\)//\(\left( {SAD} \right)\).(5)
Lại có \(\left\{ \begin{array}{l}MQ,QG \subset \left( {MQG} \right)\\MQ \cap QG = \left\{ Q \right\}\end{array} \right.\)(6)
Từ (4), (5), (6) ta suy ra (MQG) song song với mặt phẳng (SAD).
Vậy MG song song với mặt phẳng (SAD).
soanvan.me
