Đề bài
Hãy tính \( x\) và \(y\) trong các hình sau:
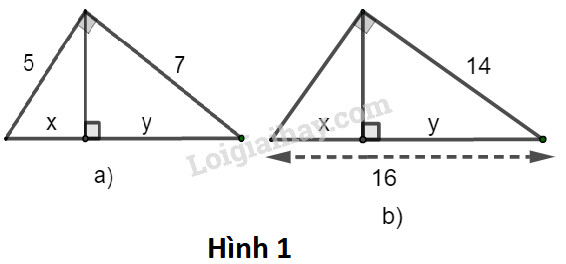
Phương pháp giải - Xem chi tiết
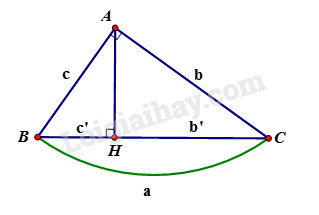
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\)
+)\(A{C^2} = CH.BC\) hay \({b^2} = ab'\)
+) \(AB^2+AC^2=BC^2\) hay \(c^2+b^2=a^2\) (định lý Pytago)
Lời giải chi tiết
a) Ta đặt tên như hình vẽ dưới đây:
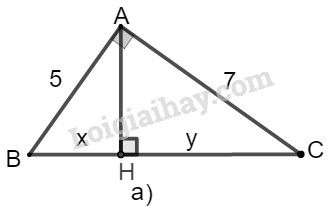
Xét tam giác \(ABC\) vuông tại A, đường cao \(AH.\)
Theo định lý Py-ta-go, ta có:
\(B{C^2}=A{C^2}+A{B^2} = {5^2} + {7^2}\)
Hay \(x + y =BC= \sqrt {{5^2} + {7^2}} = \sqrt {74} \)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
\(A{B^2} = BH.BC\)
\(\Rightarrow {5^2} = x.\sqrt {74} \Rightarrow x = \dfrac{{25}}{{\sqrt {74}}}\)
Thay \(x = \dfrac{{25}}{{\sqrt {74}}}\) vào \(x + y = \sqrt {74} \), ta có:
\(y + \dfrac{{25}}{{\sqrt {74} }} = \sqrt {74}\)\( \Rightarrow y = \sqrt {74} - \dfrac{{25}}{{\sqrt {74}}}\)\(= \dfrac{{74 - 25}}{{\sqrt {74} }} = \dfrac{{49}}{{\sqrt {74} }}\)
Vậy \(x = \dfrac{{25}}{{\sqrt {74}}};\)\(y= \dfrac{{49}}{{\sqrt {74} }}.\)
b) Ta đặt tên như hình vẽ dưới đây:
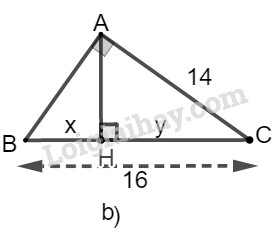
Xét tam giác \(ABC\) vuông tại A, đường cao \(AH.\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(A{C^2} = CH.BC\)
\(\Rightarrow {14^2} = y.16 \Rightarrow y = \dfrac{{{{14}^2}}}{{16}}\)\( = \dfrac{{196}}{{16}} = 12,25\)
Mà \(x + y = 16 \Rightarrow x = 16 - y \)\(= 16 - 12,25 = 3,75\)
Vậy \(x=12,25;y=3,75.\)
