Đề bài
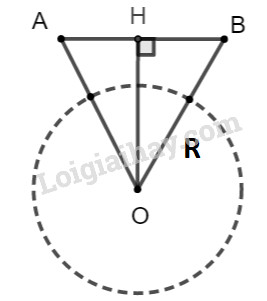
Hai vệ tinh đang bay ở vị trí \(A\) và \(B\) cùng cách mặt đất \(230km\) có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là \(2200km\)? Biết rằng bán kính \(R\) của Trái Đất gần bằng \(6370km\) và hai vệ tinh nhìn thấy nhau nếu \(OH > R\).
Phương pháp giải - Xem chi tiết
Sử dụng: Tam giác \(ABC\) vuông tại \(A\), ta có \(AB^2+AC^2=BC^2\) (định lý Pytago).
Lời giải chi tiết
Vì hai vệ tinh cùng cách mặt đất \(230km\) nên tam giác \(AOB\) cân tại O.
Ta có: \(OA = R + 230\)
\( = 6370 + 230 = 6600(km)\)
Trong tam giác cân AOB ta có: \(OH \bot AB\) nên \(H\) là trung điểm của \(AB\)
Suy ra: \(HA = HB = \dfrac{{AB}}{2}\)\( = \dfrac{{2200}}{2} = 1100(km)\)
Áp dụng định lí Pytago vào tam giác vuông \(AHO\) ta có: \(A{O^2} = A{H^2} + O{H^2}\)
Suy ra: \(O{H^2} = O{A^2} - A{H^2}\)
Suy ra:
\(\eqalign{
& OH = \sqrt {O{A^2} - A{H^2}} \cr
& = \sqrt {{{6600}^2} - {{1100}^2}} \cr
& = \sqrt {42350000} \approx 6508(km) \cr} \)
Vì \(OH > R\) nên hai vệ tinh nhìn thấy nhau.
soanvan.me
