Đề bài
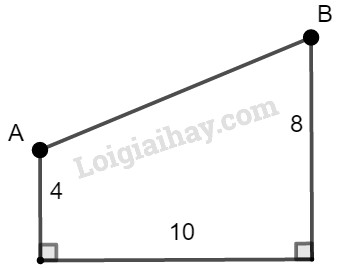
Giữa hai tòa nhà ( kho và phân xưởng) của một nhà máy, người ta xây dựng một băng chuyền \(AB\) để chuyển vật liệu. Khoảng cách giữa hai tòa nhà là \(10m\), còn hai vòng quay của băng chuyền được đặt ở độ cao \(8m\) và \(4m\) so với mặt đất (h.7). Tìm độ dài \(AB\) của băng chuyền.
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
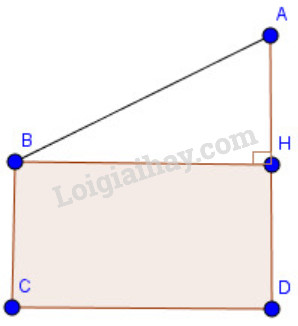
Kẻ \(BH \bot AD\) ta được tứ giác \(BCDH\) là hình chữ nhật (vì \(\widehat C=\widehat D= \widehat H=90^0).\)
Suy ra \( DH=BC=4m\) và \(BH = CD=10m\) (tính chất hình chữ nhật)
Và \(AH =AD-DH= 8 - 4 = 4\)(m)
Áp dụng định lý Pytago vào tam giác vuông \(ABH\), ta có:
\(A{B^2} = B{H^2} + A{H^2}\)
Suy ra: \(AB = \sqrt {B{H^2} + A{H^2}}\)\( = \sqrt {{{10}^2} + {4^2}} = \sqrt {116} \approx 10,8(m)\)
Vậy băng chuyền dài khoảng \(10,8m.\)
soanvan.me
