Đề bài
Cho tam giác vuông với các cạnh góc vuông có độ dài là \(5\) và \(7\), kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng và nó chia ra trên cạnh huyền.
Phương pháp giải - Xem chi tiết
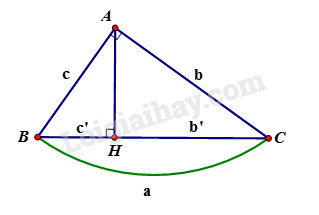
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\)
+) \(A{C^2} = CH.BC\) hay \({b^2} = ab'\)
+) \(AH^2=HB.HC;AB.AC=AH.BC\)
+) \(AB^2+AC^2=BC^2\) hay \(c^2+b^2=a^2\) (định lý Pytago)
Lời giải chi tiết
Ta vẽ được hình dưới đây:
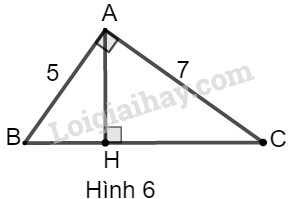
Giả sử tam giác ABC có: \(\widehat {BAC} = 90^\circ \)
\(AB = 5,AC = 7\)
Theo định lý Py-ta-go, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
\(\eqalign{
& \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} \cr
& = \sqrt {{5^2} + {7^2}} = \sqrt {74} \cr} \)
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
\(\eqalign{
& AH.BC = AB.AC \cr
& \Rightarrow AH = {{AB.AC} \over {BC}} \cr
& = {{5.7} \over {\sqrt {74} }} = {{35} \over {\sqrt {74} }} \cr} \)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
\(\eqalign{
& A{B^2} = BH.BC \cr
& \Rightarrow BH = {{A{B^2}} \over {BC}} \cr
& = {{{5^2}} \over {\sqrt {74} }} = {{25} \over {\sqrt {74} }} \cr} \)
\(\eqalign{
& CH = BC - BH \cr
& = \sqrt {74} - {{25} \over {\sqrt {74} }} = {{74 - 25} \over {\sqrt {74} }} = {{49} \over {\sqrt {74} }} \cr} \)
soanvan.me
