Đề bài
Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH :\) \(AB = c, AC = b, BC = a,\)\( AH = h, BH = c', CH = b'.\)
a) Tính \(h, b, c\) nếu biết \(b' = 36, c' = 64\).
b) Tính \(h, b, b', c'\) nếu biết \(a = 9, c = 6\).
Phương pháp giải - Xem chi tiết
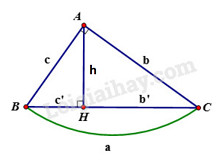
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\)
+) \(A{C^2} = CH.BC\) hay \({b^2} = ab'\)
+) \(AH^2=HB.HC;AB.AC=AH.BC\) hay \(h^2=b'.c';a.h=b.c\)
+) \(A{H^2} = BH.CH\) hay \({h^2} = b'.c'\)
Lời giải chi tiết

a) Áp dụng các hệ thức lượng trong tam giác vuông ta có:
Ta có
\(\begin{array}{l}
{h^2} = b'.c' = 36.64 = 2304\\
\Rightarrow h = 48
\end{array}\)
\(\begin{array}{l}
{b^2} =b'.a= b'(b' + c') \\= 36.(36 + 64) = 3600\\
\Rightarrow b = 60
\end{array}\)
\(\begin{array}{l}
{c^2}=c'.a = c'(b' + c') \\= 64.(36 + 64) = 6400\\
\Rightarrow c = 80
\end{array}\)
b) Áp dụng các hệ thức lượng trong tam giác vuông ta có:
+ \(c^2=c'.a\)
\(\Rightarrow c' = \dfrac{{{c^2}}}{a} = \dfrac{{{6^2}}}{9} = 4\),
+ \(b' = a - c' = 9 - 4 = 5\),
+ \({b^2} = a.b' = 9 . 5 = 45\) nên \(b = 3\sqrt 5\);
+ \({h^2} = b'.c' = 5.4=20\) nên \(h = 2\sqrt 5 \).
soanvan.me
