Đề bài
Một tam giác vuông có cạnh huyền là \(5\) và đường cao ứng với cạnh huyền là \(2\). Hãy tính cạnh nhỏ nhất của tam giác vuông này.
Phương pháp giải - Xem chi tiết
Xét tam giác \(ABC\) có \(\widehat {BAC} = {90^0},\)\(AH \bot BC,BC = 5,AH = 2\) và \(BH < CH\)
Suy luận để có \(BH + CH = 5\)
Sử dụng hệ thức: \(BH.CH = A{H^2}\)
Từ đó tính được \(BH,\) suy ra cạnh \(AB\) và lập luận để có \(AB\) là cạnh nhỏ nhất.
Lời giải chi tiết
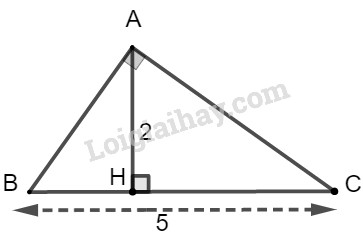
Giả sử tam giác \(ABC\) có \(\widehat {BAC} = {90^0},\)\(AH \bot BC,BC = 5,AH = 2\) và \(BH < CH\)
Ta có: \(BH + CH =BC= 5\) nên \(BH=5-CH\) (1)
Theo hệ thức liên hệ giữa đường cao và các hình chiếu cạnh góc vuông trong tam giác vuông, ta có:
\(BH.CH = A{H^2} = {2^2} = 4\) (2)
Từ (1) và (2) suy ra:
\(BH(5 - BH) = 4\)
\(\Leftrightarrow B{H^2} - 5BH + 4 = 0\)
\(\Leftrightarrow B{H^2} - 4BH -BH+ 4 = 0\)
\(\Leftrightarrow BH (BH-4 )-(BH-4) = 0\)
\(\Leftrightarrow (BH-1)(BH-4)=0\)
\(\Leftrightarrow \left[ \begin{array}{l}
BH = 1 \Rightarrow CH = 4\\
BH = 4 \Rightarrow CH = 1
\end{array} \right.\)
Do \(BH < CH\) nên \(BH = 1\) và \(CH = 4\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(A{B^2} = BH.BC \)\(= 1.5 = 5\)
Suy ra: \(AB = \sqrt 5 .\)
Vì \(BH<CH\) nên \(AB<AC\) hay \(AB=\sqrt 5\) là cạnh nhỏ nhất của tam giác \(ABC.\)
soanvan.me
