Đề bài
Cho tam giác ABC vuông tại A. Biết rằng \(\dfrac{{AB} }{{AC}} = \dfrac{5}{6}\), đường cao \(AH = 30cm\). Tính \(HB, HC\).
Phương pháp giải - Xem chi tiết
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\).
Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\)
+) \(A{C^2} = CH.BC\)
+) \(AH^2=HB.HC;AB.AC=AH.BC\)
+) \(AB^2+AC^2=BC^2\) (định lý Pytago).
Lời giải chi tiết
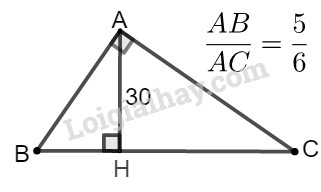
Xét hai tam giác vuông \(AHB\) và \(CHA,\) ta có:
\(\widehat {AHB} = \widehat {CHA} = {90^0}\)
\(\widehat {ABH} = \widehat {CAH}\) (hai góc cùng phụ \(\widehat {ACB}\))
Vậy \( ∆AHB \backsim ∆CHA\) (g.g)
Suy ra: \(\dfrac{{AH}}{{HC}} = \dfrac{{AB}}{{CA}}.\) (1)
Theo đề bài: \(\dfrac{{AB}}{{AC}} = \dfrac{5}{6}\) và \(AH = 30(cm)\) (2)
Từ (1) và (2) suy ra: \(\dfrac{{30}}{{HC}} = \dfrac{5 }{6} \Rightarrow HC = \dfrac{{30.6}}{5} = 36(cm)\)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(A{H^2} = HB.HC \)\(\Rightarrow HB = \dfrac{{A{H^2}}}{{HC}} = \dfrac{{{{30}^2}}}{{36}} = 25(cm)\)
soanvan.me
