Đề bài
Cho hai đoạn thẳng có độ dài là \(a\) và \(b\). Dựng đoạn thẳng \(\sqrt {ab} \) như thế nào?
Phương pháp giải - Xem chi tiết
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\).
Khi đó ta có hệ thức sau: \(AH^2=BH.CH\)
Từ đó suy ra cách dựng hình thỏa mãn đề bài.
Lời giải chi tiết
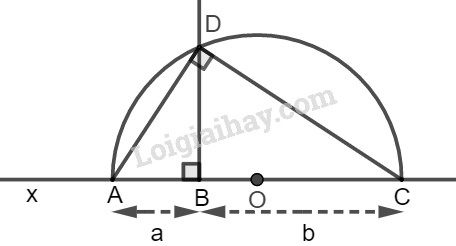
* Cách dựng:
− Dựng đường thẳng \(x\).
− Trên đường thẳng \(x\) dựng liên tiếp hai đoạn thẳng \(AB = a\), \(BC = b\).
− Dựng nửa đường tròn tâm \(O\) đường kính \(AC\).
− Từ \(B\) dựng đường thẳng vuông góc với \(AC\) cắt nửa đường tròn tâm \(O\) tại \(D\).
Ta có đoạn \(BD = \sqrt {ab} \) cần dựng.
* Chứng minh:
Nối \(DA\) và \(DC.\) Ta có tam giác \(ACD\) vuông tại \(D\) (do \(OD=OA=OC=\dfrac {AC}{2})\) và \(DB \bot AC\).
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(B{D^2} = AB.BC = a.b\)
Suy ra: \(BD = \sqrt {ab} .\)
soanvan.me
