Đề bài
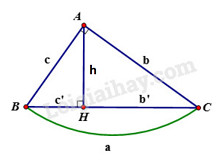
Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH :\) \(AB = c, AC = b, BC = a,\)\( AH = h, BH = c', CH = b'.\)
Chứng minh rằng:
a) \(h = \dfrac{{bc}}{a}\);
b) \(\dfrac{{{b^2}}}{{{c^2}}} = \dfrac{{b'}}{{c'}}.\)
Phương pháp giải - Xem chi tiết
Để chứng minh các công thức:
- Sử dụng công thức tính diện tích tam giác \(S = \dfrac{1}{2}ah = \dfrac{1}{2}bc.\)
- Sử dụng hệ thức lượng trong tam giác vuông:
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\)
+) \(A{C^2} = CH.BC\)
- Hoặc sử dụng tam giác đồng dạng.
Lời giải chi tiết
a) Cách 1: Dùng công thức tính diện tích tam giác vuông \(ABC\):
\(S = \dfrac{1}{2}ah = \dfrac{1}{2}bc\) suy ra \(h = \dfrac{{bc}}{ a}.\)
Cách 2: Dùng tam giác đồng dạng.
Ta có \(∆ABC \backsim ∆HBA\,(g-g)\) (do có góc B chung và \(\widehat{BAC}=\widehat {AHB}=90^0) \) suy ra \(\dfrac{{AC}}{{HA}} = \dfrac{{BC}}{ {BA}}\) tức là \(\dfrac{b}{ h} = \dfrac{a}{c}\), hay \(h = \dfrac{{bc}}{a}.\)
b) Theo hệ thức lượng trong tam giác vuông ta có: \({b^2} = ab',{c^2} = ac'\) suy ra \(\dfrac{{{b^2}}}{{{c^2}}} = \dfrac{{ab'}}{{ac'}}= \dfrac{{b'}}{{c'}}.\)
soanvan.me
