Câu hỏi 1 :
Tìm đạo hàm của hàm số \(y = 2\cos x\)
- A \(y' = 2\sin x\)
- B \(y' = - \sin x\)
- C \(y' = \sin x\)
- D \(y' = - 2\sin x\)
Đáp án: D
Phương pháp giải:
\(\left( {\cos x} \right)' = - \sin x\)
Lời giải chi tiết:
\({(2\cos x)^\prime } = 2.\left( {\cos x} \right)' = - 2\sin x\)
Câu hỏi 2 :
Tìm đạo hàm của hàm số \(y = \tan x\) với \(x \ne \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
- A \(y' = \dfrac{1}{{{{\sin }^2}x}}\).
- B \(y{\rm{'}} = \dfrac{1}{{{{\sin }^2}x}}\).
- C \(y{\rm{'}} = - \dfrac{1}{{{{\cos }^2}x}}\).
- D \(y{\rm{'}} = \dfrac{1}{{{{\cos }^2}x}}\).
Đáp án: D
Phương pháp giải:
Đạo hàm của hàm lượng giác.
Lời giải chi tiết:
\(y' = \dfrac{1}{{{{\cos }^2}x}}\)
Câu hỏi 3 :
Cho hình hộp ABCD.A’B’C’D’ (hình vẽ minh họa).
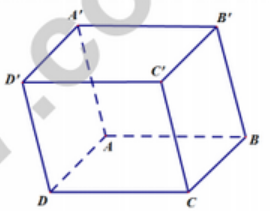
Mệnh đề nào sau đây đúng?
- A \(\overrightarrow {A{C^\prime }} = \overrightarrow {AD} + \overrightarrow {AC} + \overrightarrow {A{A^\prime }} \)
- B \(\overrightarrow {A{C^\prime }} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} \)
- C \(\overrightarrow {A{C^\prime }} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{A^\prime }} \).
- D \(\overrightarrow {A{C^\prime }} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC} \).
Đáp án: B
Phương pháp giải:
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết:
ACC’A’ và ABCD là hình bình hành nên: \(\overrightarrow {A{C^\prime }} = \overrightarrow {AC} + \overrightarrow {A{A^\prime }} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} \)
Câu hỏi 4 :
Trong không gian, cho đoạn thẳng AB có trung điểm là I, \((\alpha )\) là mặt phẳng trung trực của đoạn thẳng AB. Phát biểu nào sau đây đúng?
- A \((\alpha )\) qua I và vuông góc với AB.
- B \((\alpha )\) qua A và vuông góc với AB.
- C \((\alpha )\) qua I và không vuông góc với AB.
- D \((\alpha )\) qua B và vuông góc với AB.
Đáp án: A
Phương pháp giải:
Định nghĩa mặt phẳng trung trực.
Lời giải chi tiết:
Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng vuông góc với AB tại trung điểm của AB.
Câu hỏi 5 :
Hàm số nào dưới đây liên tục trên toàn bộ tập số thực \(\mathbb{R}\) ?
- A \(y = \tan x\).
- B \(y = \dfrac{{x - 1}}{{2x + 1}}\).
- C \(y = {x^2} - 3x + 56\).
- D \(y = \dfrac{1}{{{x^2} - 2}}\).
Đáp án: C
Phương pháp giải:
Hàm đa thức luôn liên tục trên \(\mathbb{R}\)
Lời giải chi tiết:
\(y = {x^2} - 3x + 56\) là hàm đa thức nên liên tục trên \(\mathbb{R}\).
Câu hỏi 6 :
Mệnh đề nào sau đây sai?
- A \({(c)^\prime } = 0\) ( \(c\) là hằng số).
- B \({(\sqrt x )^\prime } = \dfrac{1}{{\sqrt x }}(x > 0)\).
- C \({\left( {{x^n}} \right)^\prime } = n{x^{n - 1}}(n \in \mathbb{N},n > 1)\).
- D \({(x)^\prime } = 1\).
Đáp án: B
Phương pháp giải:
Sử dụng quy tắc đạo hàm các hàm cơ bản.
Lời giải chi tiết:
B sai vì \(\left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\).
Câu hỏi 7 :
\(\mathop {\lim }\limits_{x \to {2^2}} \dfrac{{2x - 5}}{{x - 2}}\) bằng
- A \( - \infty \)
- B \(\dfrac{5}{2}\).
- C \( + \infty \)
- D 2
Đáp án: A
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = L < 0;\mathop {\lim }\limits_{x \to {x_0}^ + } g\left( x \right) = 0\) và \(g\left( x \right) > 0\) khi \(x \to {x_0}^ + \) thì \(\mathop {\lim }\limits_{x \to x_0^ + } \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = - \infty \)
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^2}} 2x - 5 = - 1 < 0\\\mathop {\lim }\limits_{x \to {2^2}} \left( {x - 2} \right) = 0;\\x - 2 > 0\forall x > 2\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {2^2}} \dfrac{{2x - 5}}{{x - 2}} = - \infty \)
Câu hỏi 8 :
Gọi \({\rm{S}}\) là tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) có công bội \(q(|q| < 1)\). Khẳng định nào sau đây đúng ?
- A \(S = \dfrac{{{u_1}}}{{1 - q}}\).
- B \(S = \dfrac{{{u_1}}}{{1 + q}}\).
- C \(S = \dfrac{1}{{{u_1} - q}}\).
- D \(S = \dfrac{{{u_1}}}{{q - 1}}\).
Đáp án: A
Phương pháp giải:
Lý thuyết tổng cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) có công bội \(q(|q| < 1)\).
Lời giải chi tiết:
\(\begin{array}{l}S = {u_1} + {u_2} + ...\\ = {u_1}\left( {1 + q + {q^2} + ...} \right)\\ = \dfrac{{{u_1}}}{{1 - q}}\end{array}\)
Câu hỏi 9 :
Cho hai hàm số \(u = u(x),v = v(x)\) có đạo hàm tại điểm \(x\) thuộc khoảng xác định. Mệnh đề nào sau đây sai ?
- A \({(u + v)^\prime } = {u^\prime } + {v^\prime }\).
- B \({(u - v)^\prime } = {u^\prime } - {v^\prime }\).
- C \({(ku)^\prime } = k{u^\prime }\) ( \(k\) là hằng số).
- D \({(uv)^\prime } = {u^\prime }{v^\prime }\).
Đáp án: D
Phương pháp giải:
Sử dụng quy tắc đạo hàm của tổng hiệu, tích.
Lời giải chi tiết:
D sai vì \(\left( {u.v} \right)' = u'.v + v'.u\)
Câu hỏi 10 :
Cho hai hàm số \(f(x),g(x)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x) = - 5\) và \(\mathop {\lim }\limits_{x \to 1} g(x) = 2\). Giá trị của \(\mathop {\lim }\limits_{x \to 1} [f(x) - g(x)]\) bằng
- A 7
- B 3
- C \( - 7\)
- D \( - 3\)
Đáp án: C
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to {x_0}} [f(x) - g(x)] = \mathop {\lim }\limits_{x \to {x_0}} f(x) - \mathop {\lim }\limits_{x \to {x_0}} g(x)\)
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} [f(x) - g(x)]\\ = \mathop {\lim }\limits_{x \to 1} f(x) - \mathop {\lim }\limits_{x \to 1} g(x)\\ = - 5 - 2 = - 7\end{array}\)
Câu hỏi 11 :
Cho lăng trụ ABC.A’B’C’(hình vẽ minh họa)
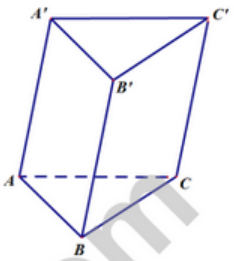
Vecto \(\overline {{A^\prime }A} \) không phải là vecto chỉ phương của đường thẳng nào sau đây?
- A BB’
- B AA’
- C BC
- D CC’
Đáp án: C
Phương pháp giải:
\(\overrightarrow {{A^\prime }A} \) là vecto chỉ phương của mọi đường thẳng song song với \({A^\prime }A\)
Lời giải chi tiết:
BC không song song với \(AA'\) nên BC không nhận \(AA'\) làm vecto chỉ phương.
Câu hỏi 12 :
Trong không gian, cho hai đường thẳng phân biệt a, b và mặt phẳng \(\alpha \). Phát hiểu nào sau đây đúng?
- A Nếu \(a//(\alpha )\) và \(b//(\alpha )\) thì \(a \bot b\).
- B Nếu \(a \bot (\alpha )\) và \(b \bot (\alpha )\) thì \(a \bot b\).
- C Nếu \(b//(\alpha )\) và \(a \bot (\alpha )\) thì \(a \bot b\).
- D Nếu \(b/4(\alpha )\) và \(a \bot b\) thì \(a \bot (\alpha )\).
Đáp án: C
Phương pháp giải:
Lý thuyết đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:
Nếu \(b//(\alpha )\) và \(a \bot (\alpha )\) thì \(a \bot b\).
Câu hỏi 13 :
Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA vuông góc với mặt phẳng (ABCD) (như hình vẽ minh họa)

Hãy chọn khẳng định đúng?
- A \(BD \bot (SAC)\).
- B \(CD \bot (SAD)\).
- C \(AC \bot (SBD)\).
- D \(BC \bot (SAB)\).
Đáp án: A
Phương pháp giải:
2 đường chéo của hình thoi vuông góc với nhau.
Lời giải chi tiết:
ABCD là hình thoi nên \(BD \bot AC\).
Mà \(BD \bot SA\) và AC và SA cắt nhau tại A nên \(BD \bot \left( {SAC} \right)\).
Câu hỏi 14 :
\(\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 4}}{{x - 2}}\) bằng
- A \( + \infty \)
- B 0
- C 2
- D 4
Đáp án: D
Phương pháp giải:
Khử mẫu. Thay x=2 tìm giới hạn.
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 4}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4\end{array}\)
Câu hỏi 15 :
\(\lim \dfrac{{n + 1}}{{2n - 3}}\) bằng
- A 0
- B \( - \infty \).
- C \(\dfrac{1}{2}\).
- D \( - \dfrac{1}{3}\).
Đáp án: C
Phương pháp giải:
Chia cả tử và mẫu cho n. Sử dụng \(\lim \dfrac{1}{n} = 0\)
Lời giải chi tiết:
\(\lim \dfrac{{n + 1}}{{2n - 3}} = \lim \dfrac{{n\left( {1 + \dfrac{1}{n}} \right)}}{{2\left( {1 - \dfrac{3}{n}} \right)}} = \dfrac{1}{2}\)
Câu hỏi 16 :
Cho hình chóp S.ABCD có đáy là hình bình hành (hình vẽ minh họa).

Hãy chọn khẳng định đúng.
- A \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
- B \(\overrightarrow {SA} + \overrightarrow {AB} = \overrightarrow {SD} + \overrightarrow {DC} \)
- C \(\overrightarrow {SA} + \overrightarrow {AD} = \overrightarrow {SB} + \overrightarrow {BC} \).
- D \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \)
Đáp án: A
Phương pháp giải:
M là trung điểm của AB thì \(\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {CM} \).
Lời giải chi tiết:
Gọi O là giao điểm của AC và BD.
Khi đó O là trung điểm chung của AC và BD.
\(\begin{array}{l}\overrightarrow {SC} + \overrightarrow {SA} = 2\overrightarrow {SO} ;\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \\ \Rightarrow \overrightarrow {SC} + \overrightarrow {SA} = \overrightarrow {SB} + \overrightarrow {SD} \end{array}\)
Câu hỏi 17 :
Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau (hình vẽ minh họa).
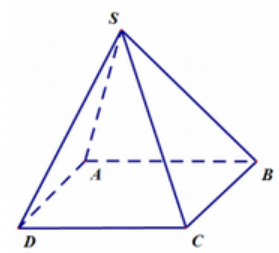
Số đo góc giữa hai đường thẳng SA và CD bằng
- A \(120^\circ \).
- B \(30^\circ \).
- C \(60^\circ \).
- D \(90^\circ \).
Đáp án: C
Phương pháp giải:
Từ một điểm trên a và kẻ đường thẳng c song song với đường thẳng b thì góc giữa a và b bằng góc giữa c và b.
Lời giải chi tiết:
\(\begin{array}{l}CD||AB \Rightarrow \widehat {\left( {SA,CD} \right)}\\ = \widehat {\left( {SA,AB} \right)} = \widehat {SAB} = 60^\circ \end{array}\)
Câu hỏi 18 :
Tìm đạo hàm của hàm số \(y = \sqrt {{x^2} + 1} \).
- A \({y^\prime } = \dfrac{{2x}}{{\sqrt {{x^2} + 1} }}\).
- B \({y^\prime } = \dfrac{x}{{\sqrt {{x^2} + 1} }}\).
- C \({y^\prime } = \dfrac{{2x + 1}}{{2\sqrt {{x^2} + 1} }}\).
- D \({y^\prime } = \dfrac{1}{{2\sqrt {{x^2} + 1} }}\).
Đáp án: B
Phương pháp giải:
Sử dụng \(\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}\)
Lời giải chi tiết:
\(y' = \dfrac{{\left( {{x^2} + 1} \right)'}}{{2\sqrt {{x^2} + 1} }} = \dfrac{{2x}}{{2\sqrt {{x^2} + 1} }} = \dfrac{x}{{\sqrt {{x^2} + 1} }}\)
Câu hỏi 19 :
Cho hàm số \(y = \sin 2x\). Mệnh đề nào sau đây đúng?
- A \({y^\prime }\left( {\dfrac{\pi }{6}} \right) = \sqrt 3 \).
- B \({y^\prime }\left( {\dfrac{\pi }{6}} \right) = - 1\).
- C \({y^\prime }\left( {\dfrac{\pi }{6}} \right) = 1\).
- D \({y^\prime }\left( {\dfrac{\pi }{6}} \right) = \dfrac{1}{2}\).
Đáp án: C
Phương pháp giải:
\(\left( {\sin u} \right)' = u'.\cos u\)
Thay \(x = \dfrac{\pi }{6}\) vào đạo hàm.
Lời giải chi tiết:
\(\begin{array}{l}y' = \left( {\sin 2x} \right)' = 2.\cos 2x\\ \Rightarrow y'\left( {\dfrac{\pi }{6}} \right) = 2.\cos \dfrac{\pi }{3} = 1\end{array}\)
Câu hỏi 20 :
Một chất điểm chuyển động theo phương trình \(S = - \dfrac{1}{3}{t^3} + 6{t^2}\), trong đó \(t > 0,t\) được tính bằng giây \((s)\) và \(S\) tính bằng mét \((m)\). Vận tốc của chất điểm tại thời điểm \(t = 3\) (giây) bằng
- A \(33m/s\)
- B \(9m/s\).
- C \(27m/s\).
- D \(3m/s\).
Đáp án: C
Phương pháp giải:
Hàm số của vận tốc: \(v\left( t \right) = S'\left( t \right)\).
Thay t=3 vào tính \(v\left( 3 \right)\).
Lời giải chi tiết:
\(\begin{array}{l}v\left( t \right) = S'\left( t \right) = - {t^2} + 12t\\ \Rightarrow v\left( 3 \right) = - 9 + 36 = 27m/s\end{array}\)
Câu hỏi 21 :
\(\lim \dfrac{{1 - {3^n}}}{{{2^n} + {{4.3}^n}}}\) bằng
- A \(\dfrac{3}{2}\).
- B 0
- C \( - \dfrac{1}{4}\).
- D \( - 1\)
Đáp án: C
Phương pháp giải:
Chia cả tử và mẫu cho \({3^n}\).
\(\lim \dfrac{1}{{{3^n}}} = 0;\lim \dfrac{{{2^n}}}{{{3^n}}} = 0\)
Lời giải chi tiết:
\(\lim \dfrac{{1 - {3^n}}}{{{2^n} + {{4.3}^n}}} = \lim \dfrac{{\dfrac{1}{{{3^n}}} - 1}}{{\dfrac{{{2^n}}}{{{3^n}}} + 4}} = \dfrac{{ - 1}}{4}\)
Câu hỏi 22 :
(2 điểm)
Câu 1:
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{\sqrt {x + 6} - 2}}{{x + 2}}}&{{\rm{ khi }}x > - 2}\\{x + 2m}&{{\rm{ khi }}x \le - 2}\end{array}} \right.\). Tìm tất cả các giá trị của tham số \(m\) để hàm số \(f(x)\) liên tục tại điểm \(x = - 2\).
Đáp án - Lời giảiCâu 2:
Cho hàm số \(y = f(x) = \dfrac{{2x - 1}}{{x + 1}}\), có đồ thị \((C)\). Viết phương trình tiếp tuyến của đồ thị \((C)\) biết tiếp tuyến vuông góc với đường thẳng \(d:y = - 3x + 4\).
Phương pháp giải:
Tìm \(f'\left( x \right)\).
Tiếp tuyến của hàm số tại \({x_0}\): \(y = f'\left( {{x_0}} \right).\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).
Lời giải chi tiết:
\(f'\left( x \right) = \dfrac{3}{{{{\left( {x + 1} \right)}^2}}}\)
Tiếp tuyến vuông góc với đường thẳng \(d:y = - 3x + 4\) nên
\(\dfrac{3}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{1}{3} \Leftrightarrow \left| {x + 1} \right| = 3\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 4\end{array} \right.\)
Câu hỏi 23 :
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, \(\alpha \) là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Xác định \(\alpha \) và tính \(\sin \alpha \).
Phương pháp giải:
Xác định đường thẳng qua G và vuông góc với (SAC).
Góc giữa CG và (SAC) là góc giữa CG và hình chiếu của nó lên (SAC).
Lời giải chi tiết:
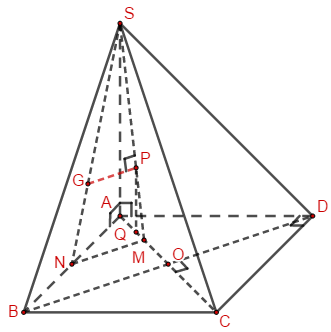
Gọi O là tâm của ABCD.
M là trung điểm của AO, N là trung điểm của AB.
Qua G kẻ GP song song với MN (\(P \in SM\)).
Ta có ABCD là hình vuông nên \(BD \bot AC\). Mà \(MN||BD\)\( \Rightarrow MN \bot AC\).
Ta lại có \(MN \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\)
=> \(MN \bot \left( {SAC} \right)\)
\(\begin{array}{l}GP||MN \Rightarrow GP \bot \left( {SAC} \right)\\ \Rightarrow \widehat {\left( {CG,\left( {SAC} \right)} \right)} = \widehat {GCP} = \alpha \end{array}\)
\(GP = \dfrac{2}{3}MN = \dfrac{2}{3}.\dfrac{1}{2}OB\)\( = \dfrac{1}{3}.\dfrac{1}{2}BD = \dfrac{1}{6}.a\sqrt 2 \)
Kẻ \(PQ||SA \Rightarrow PQ = \dfrac{1}{3}SA = \dfrac{{2a}}{3}\)
\(\begin{array}{l}CQ = \dfrac{1}{3}MA + 3MA = \dfrac{{10}}{3}.MA\\ = \dfrac{{10}}{3}.\dfrac{1}{4}AC = \dfrac{5}{6}AC = \dfrac{{5.a\sqrt 2 }}{6}\\ \Rightarrow CP = \sqrt {C{Q^2} + P{Q^2}} \\ = \sqrt {\dfrac{{25{a^2}}}{{18}} + \dfrac{{4{a^2}}}{9}} = a\sqrt {\dfrac{{11}}{6}} \\ \Rightarrow CG = \sqrt {C{P^2} + G{P^2}} = \dfrac{{a\sqrt {17} }}{3}\\ \Rightarrow \sin \alpha = \dfrac{{GP}}{{CG}} = \dfrac{{\sqrt 2 }}{6}.\dfrac{3}{{\sqrt {17} }} = \dfrac{1}{{\sqrt {34} }}\end{array}\)
