Câu hỏi 1 :
Trong các khẳng định sau, khẳng định nào sai:
- A \(\lim {(\sqrt 2 )^n} = 0\)
- B \(\lim {\left( {\dfrac{1}{3}} \right)^n} = 0\)
- C \(\lim {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^n} = 0\)
- D \(\lim {\left( {\dfrac{4}{3}} \right)^n} = + \infty \)
Đáp án: A
Phương pháp giải:
\(q > 1 = > \lim {q^n} = + \infty \)
Lời giải chi tiết:
\(\sqrt 2 > 1 = > \lim {(\sqrt 2 )^n} = + \infty \)
Đáp án A sai.
Câu hỏi 2 :
\(\mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3x} \right)\) bằng
- A 3
- B \( - \infty \)
- C 2
- D \( + \infty .\)
Đáp án: D
Phương pháp giải:
Đưa \({x^3}\) ra ngoài.
\(\mathop {\lim }\limits_{x \to - \infty } {x^{2k + 1}} = - \infty ,k \in \mathbb{Z}\)
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty ,k < 0\)\( = > \mathop {\lim }\limits_{x \to - \infty } k.f\left( x \right) = + \infty \)
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3x} \right) = \mathop {\lim }\limits_{x \to - \infty } {x^3}.\left( { - 1 + \dfrac{3}{{{x^2}}}} \right) = + \infty \)
Câu hỏi 3 :
Tiếp tuyến của đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 1\) tại điểm \(M( - 1; - 4)\) có hệ số góc bằng
- A 5
- B 12
- C 7
- D \( - 1\)
Đáp án: B
Phương pháp giải:
\(f'\left( {{x_0}} \right)\) là hệ số góc của tiếp tuyến đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\).
Lời giải chi tiết:
\(\begin{array}{l}y' = 6{x^2} - 6x\\y'\left( { - 1} \right) = 12\end{array}\)
Câu hỏi 4 :
Cho \(u = u(x)\) và \(v = v(x)\) là các hàm số có đạo hàm. Khẳng định nào sau đây sai
- A \((uv)' = u'v + v'u\).
- B \((u + v)' = {u^\prime } + {v^\prime }\).
- C \((u - v)' = u' - {v^\prime }\)
- D \({\left( {\dfrac{u}{v}} \right)^\prime } = \dfrac{{u'v + v'u}}{{{v^2}}}\).
Đáp án: D
Phương pháp giải:
Sử dụng quy tắc đạo hàm.
Lời giải chi tiết:
\({\left( {\dfrac{u}{v}} \right)^\prime } = \dfrac{{uv - vu}}{{{v^2}}}\)
Câu hỏi 5 :
Cho hình lập phương \(ABCD,{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có cạnh bằng 3a. Khoảng cách từ \({A^\prime }\) đến mặt phẳng \((ABCD)\) bằng
- A \(a\)
- B 2a
- C \(\dfrac{a}{2}\).
- D 3a.
Đáp án: D
Phương pháp giải:
Cạnh bên hình lập phương vuông góc với 2 đáy.
Lời giải chi tiết:
Ta có \(A'A \bot \left( {ABCD} \right) \Rightarrow d\left( {A',\left( {ABCD} \right)} \right) = A'A\)=3a
Câu hỏi 6 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot (ABCD)\). Mệnh đề nào đưới đây sai?
- A \(CD \bot (SAD)\).
- B \(BC \bot (SAB)\).
- C \(AC \bot (SBD)\).
- D \(BD \bot (SAC)\).
Đáp án: C
Phương pháp giải:
Xét từng đáp án.
Sử dụng lý thuyết:
Đường thẳng vuông góc với một mặt phẳng thì vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Lời giải chi tiết:
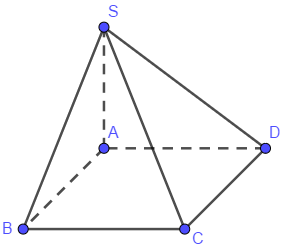
Đáp án C sai vì nếu \(AC \bot (SBD)\) thì \(AC \bot SO\left( {\left\{ O \right\} = AC \cap BD} \right)\)
Điều này không thể xảy ra vì từ S chỉ có thể kẻ được 1 đường thẳng \(SA \bot AC\).
Câu hỏi 7 :
Đạo hàm của hàm số \(y = x + {\sin ^2}x\) là
- A \(1 + 2\sin x\).
- B \(1 + \sin 2x\).
- C \(1 + 2\cos x\)
- D \(2\cos x\).
Đáp án: B
Phương pháp giải:
\(\left( {\sin x} \right)' = \cos x\)
Lời giải chi tiết:
\(y' = x' + \left( {{{\sin }^2}x} \right)'\)\( = 1 + 2.\sin x.\cos x = 1 + \sin 2x\)
Câu hỏi 8 :
Đạo hàm của hàm số \(y = {(5x - 1)^2}\) là
- A \({y^\prime } = 50x - 1\).
- B \({y^\prime } = 50x - 10\).
- C \({y^\prime } = 10x - 5\).
- D \({y^\prime } = 10x - 1\).
Đáp án: B
Phương pháp giải:
\(\left( {{u^n}} \right)' = n.u'.{u^{n - 1}}\)
Lời giải chi tiết:
\(y' = 2.5.\left( {5x - 1} \right) = 50x - 10\)
Câu hỏi 9 :
Trong không gian, cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) bằng
- A \(\overrightarrow {AC'} \)
- B \(\overrightarrow {AD'} \).
- C \(\overrightarrow {AB'} \)
- D \(\overrightarrow {AC} \).
Đáp án: A
Phương pháp giải:
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết:
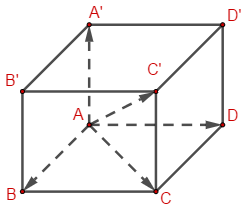
ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(ACC'A'\) là hình bình hành \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Câu hỏi 10 :
Đạo hàm của hàm số \(y = \cos 2x\) là
- A \( - 2\sin x\).
- B \( - 2\sin 2x\).
- C \(2\sin 2x\)
- D \(2\cos 2x\).
Đáp án: B
Phương pháp giải:
\(\left( {\cos u} \right)' = - u'.\sin u\)
Lời giải chi tiết:
\(y' = - 2.\sin 2x\)
Câu hỏi 11 :
\(\mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{2x - 1}}{{3 - x}}\) bằng
- A 1
- B \( - \infty \).
- C 0
- D \( + \infty \).
Đáp án: B
Phương pháp giải:
\(\begin{array}{l}\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L > 0;\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\\g\left( x \right) < 0khix \to {x_0}\end{array} \right.\\ \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = - \infty \end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ + }} 2x - 1 = 5 > 0\\\mathop {\lim }\limits_{x \to {3^ + }} 3 - x = 0\\3 - x < 0khix \to {3^ + }\\ \Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{2x - 1}}{{3 - x}} = - \infty \end{array}\)
Câu hỏi 12 :
Trong không gian cho điểm \(A\) và mặt phẳng \((P)\). Mệnh đề nào đưới đây đúng ?
- A Có đúng một mặt phẳng đi qua \(A\) và vuông góc với \((P)\).
- B Có đúng hai mặt phẳng đi qua \(A\) và vuông góc với \((P)\).
- C Có vô số mặt phẳng đi qua \(A\) và vuông góc với \((P)\).
- D Không tồn tại mặt phẳng đi qua \(A\) và vuông góc với \((P)\).
Đáp án: C
Phương pháp giải:
Lý thuyết hai đường thẳng vuông góc.
Lời giải chi tiết:
Có vô số mặt phẳng qua A và vuông góc với \((P)\).
Câu hỏi 13 :
Cho hàm số \(y = f(x)\) có đồ thị \((C)\). Phương trình tiếp tuyến của \((C)\) tại điểm \(M\left( {{x_0};{y_0}} \right)\) là
- A \(y + {y_0} = {f^\prime }\left( {{x_0}} \right)\left( {x + {x_0}} \right)\).
- B \(y + {y_0} = {f^\prime }\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
- C \(y - {y_0} = {f^\prime }\left( {{x_0}} \right)\left( {x + {x_0}} \right)\).
- D \(y - {y_0} = {f^\prime }\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
Đáp án: D
Phương pháp giải:
Lý thuyết phương trình tiếp tuyến.
Lời giải chi tiết:
\(\begin{array}{l}y = {f^\prime }\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\\ \Rightarrow y - {y_0} = {f^\prime }\left( {{x_0}} \right)\left( {x - {x_0}} \right)\end{array}\)
Câu hỏi 14 :
Đạo hàm của hàm số \(y = \dfrac{1}{{{x^2}}}\) là
- A \( - \dfrac{1}{{{x^3}}}\).
- B \( - \dfrac{1}{x}\).
- C \( - \dfrac{2}{{{x^3}}}\).
- D \( - \dfrac{1}{{{x^4}}}\).
Đáp án: C
Phương pháp giải:
\(\left( {{x^a}} \right)' = a.{x^{a - 1}}\)
Lời giải chi tiết:
\(\begin{array}{l}\dfrac{1}{{{x^2}}} = {x^{ - 2}}\\ \Rightarrow y' = \left( {{x^{ - 2}}} \right)' = - 2.{x^{ - 3}} = \dfrac{{ - 2}}{{{x^3}}}\end{array}\)
Câu hỏi 15 :
Đạo hàm của hàm số \(y = 2\sin x - 3\cos x\) là
- A \(3\sin x + 2\cos x\).
- B \(3\sin x - 2\cos x\)
- C \( - 3\sin x - 2\cos x\).
- D \( - 3\sin x + 2\cos x\)
Đáp án: A
Phương pháp giải:
\(\left( {\sin x} \right)' = \cos x;\left( {\cos x} \right)' = - \sin x\)
Lời giải chi tiết:
\(y' = \left( {2\sin x - 3\cos x} \right)'\)\( = 2.\cos x + 3\sin x\)
Câu hỏi 16 :
Cho \(\left( {{u_n}} \right)\) là cấp số nhân với \({u_1} = 3\) và công bội \(q = - \dfrac{1}{2}\). Gọi \({S_n}\) là tổng của \(n\) số hạng đầu tiên của cấp số nhân đã cho. Ta có \(\lim {S_n}\) bằng
- A 2
- B \(\dfrac{1}{2}\).
- C 6
- D \(\dfrac{3}{2}\).
Đáp án: A
Phương pháp giải:
\(\lim {S_n} = \dfrac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết:
\(\lim {S_n} = \dfrac{{{u_1}}}{{1 - q}} = \dfrac{3}{{1 + \dfrac{1}{2}}} = 2\)
Câu hỏi 17 :
Cho hàm số \(f(x)\) có đạo hàm \({f^\prime }(x) = 2x + 4\) với mọi \(x \in \mathbb{R}\). Hàm số \(g(x) = 2f(x) + 3x - 1\) có đạo hàm là
- A x+2
- B 2x+6
- C 4x+8
- D 4x+11
Đáp án: D
Phương pháp giải:
\(\left[ {f\left( x \right) + g\left( x \right)} \right]' = f'\left( x \right) + g'\left( x \right)\)
Lời giải chi tiết:
\(g'\left( x \right) = 2.f'\left( x \right) + 3\)\( = 2.\left( {2x + 4} \right) + 3 = 4x + 11\)
Câu hỏi 18 :
Cho hàm số \(f(x) = {(2x - 1)^3}\). Giá trị của \({f^\prime }(1)\) bằng
- A 12
- B 6
- C 24
- D 4
Đáp án: B
Phương pháp giải:
\(\left( {{u^n}} \right)' = n.u'.{u^{n - 1}}\)
Thay x=1 vào tính f’(1).
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = 3.2.{\left( {2x - 1} \right)^2} = 6.{\left( {2x - 1} \right)^2}\\f'\left( 1 \right) = 6\end{array}\)
Câu hỏi 19 :
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng \(a\sqrt 2 \). Khoảng cách từ điểm \(S\) đến mặt phẳng (ABCD) bằng
- A 2a.
- B \(\sqrt 3 a\).
- C a
- D \(\sqrt 2 a\).
Đáp án: C
Phương pháp giải:
Tính đường chéo AC.
Hình chóp đều có đáy là hình vuông và hình chiếu của S đến (ABCD) là tâm của đáy.
Lời giải chi tiết:
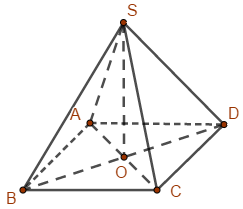
Gọi O là giao điểm của AC và BD.
Khi đó \(d\left( {S,\left( {ABCD} \right)} \right) = SO\)
ABCD là hình vuông nên
\(\begin{array}{l}AC = a\sqrt 2 .\sqrt 2 = 2a = > AO = a\\ = > S{O^2} = S{A^2} - A{O^2} = 2{a^2} - {a^2} = {a^2}\\ = > SO = a\end{array}\)
Câu hỏi 20 :
Cho hai dãy \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) thỏa mãn \(\lim {u_n} = - 5\) và \(\lim {v_n} = 4\). Giá trị của \(\lim \left( {3{u_n} + 4{v_n}} \right)\) bằng
- A 1
- B 6
- C 5
- D \( - 1\)
Đáp án: A
Phương pháp giải:
\(\lim {u_n} = M;\lim {v_n} = N\)\( \Rightarrow \lim \left( {a{u_n} + b{v_n}} \right) = a.M + b.N\)
Lời giải chi tiết:
\(\lim \left( {3{u_n} + 4{v_n}} \right) = 3.\left( { - 5} \right) + 4.4 = 1\)
Câu hỏi 21 :
Giá trị thực của tham số \(m\) để hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{x^2} - 1}&{{\rm{ khi }}x > 2}\\{m + 1}&{{\rm{ khi }}x \le 2}\end{array}} \right.\) liên tục tại \(x = 2\) bằng
- A 5
- B 2
- C 3
- D 1
Đáp án: B
Phương pháp giải:
\(f\left( x \right)\) liên tục tại \({x_0}\)\( \Leftrightarrow f\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\)
Lời giải chi tiết:
\(\begin{array}{l}f\left( 2 \right) = \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = m + 1\\\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {{x^2} - 1} \right) = 3\\ \Rightarrow m + 1 = 3 \Leftrightarrow m = 2\end{array}\)
Câu hỏi 22 :
\(\lim \left( {\dfrac{2}{n} + \dfrac{3}{{{n^2}}}} \right)\) bằng
- A 1
- B 0
- C \( + \infty \).
- D \(\dfrac{1}{2}\).
Đáp án: B
Phương pháp giải:
\(\lim \dfrac{1}{{{n^k}}} = 0\forall k \ge 1\)
Lời giải chi tiết:
\(\lim \left( {\dfrac{2}{n} + \dfrac{3}{{{n^2}}}} \right) = 0\)
Câu hỏi 23 :
Đạo hàm của hàm số \(y = 4\sqrt x \) tại điểm \(x = 4\) bằng
- A 9
- B 6
- C 1
- D 3
Đáp án: C
Phương pháp giải:
\(\left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\)
Thay x=4 vào tính đạo hàm.
Lời giải chi tiết:
\(y' = 4.\left( {\sqrt x } \right)' = \dfrac{2}{{\sqrt x }} \Rightarrow y'\left( 4 \right) = 1\)
Câu hỏi 24 :
\(\mathop {\lim }\limits_{x \to 1} \left( { - {x^2} + 3x - 2} \right)\) bằng
- A 1
- B \( - 1\)
- C \( - \infty \).
- D 0
Đáp án: D
Phương pháp giải:
Thay x=1 vào tính giới hạn.
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to 1} \left( { - {x^2} + 3x - 2} \right) = - {1^2} + 3.1 - 2 = 0\)
Câu hỏi 25 :
Đạo hàm của hàm số \(y = \dfrac{{2x - 3}}{{3x - 2}}\) là
- A \(\dfrac{5}{{{{(3x - 2)}^2}}}\).
- B \(\dfrac{{ - 5}}{{{{(3x - 2)}^2}}}\).
- C \(\dfrac{{ - 13}}{{{{(3x - 2)}^2}}}\).
- D \(\dfrac{6}{{{{(3x - 2)}^2}}}\).
Đáp án: A
Phương pháp giải:
\({\left( {\dfrac{u}{v}} \right)^\prime } = \dfrac{{u'.v - v'.u}}{{{v^2}}}\)
Lời giải chi tiết:
\(\begin{array}{l}y' = \dfrac{{\left( {2x - 3} \right)'.\left( {3x - 2} \right) - \left( {3x - 2} \right)'\left( {2x - 3} \right)}}{{{{\left( {3x - 2} \right)}^2}}}\\ = \dfrac{{2.\left( {3x - 2} \right) - 3.\left( {2x - 3} \right)}}{{{{\left( {3x - 2} \right)}^2}}}\\ = \dfrac{5}{{{{\left( {3x - 2} \right)}^2}}}\end{array}\)
Câu hỏi 26 :
Đạo hàm của hàm số \(y = \sin x - x\cos x\) là
- A \(x\sin x\).
- B \( - x\sin x\).
- C \(\sin x + \cos x\)
- D \(2\cos x - x\sin x\)
Đáp án: A
Phương pháp giải:
\(\left( {\sin x} \right)' = \cos x;\left( {\cos x} \right)' = - \sin x\)
Lời giải chi tiết:
\(y = \cos x - \cos x - x.\left( { - \sin x} \right) = x.\sin x\)
Câu hỏi 27 :
Trong không gian, với \(\vec a,\vec b\) là hai vectơ bất kỳ, mệnh đề nào dưới đây đúng ?
- A \(\vec a\vec b = |\vec a||\vec b|\).
- B \(\vec a\vec b = - |\vec a||\vec b|\cos (\vec a,\vec b)\).
- C \(\vec a\vec b = |\vec a||\vec b|\sin (\vec a,\vec b)\).
- D \(\vec a\vec b = |\vec a||\vec b|\cos (\vec a,\vec b)\).
Đáp án: D
Phương pháp giải:
Lý thuyết tích vô hướng của 2 vecto.
Lời giải chi tiết:
\(\vec a\vec b = |\vec a||\vec b|\cos (\vec a,\vec b)\)
Câu hỏi 28 :
Đạo hàm cấp hai của hàm số \(y = 3{x^2} - 2021x + 2020\) là
- A 6
- B 2020
- C 2021
- D 0
Đáp án: A
Phương pháp giải:
Tính y’, y’’=(y’)’
Lời giải chi tiết:
\(\begin{array}{l}y' = 6x - 2021\\ \Rightarrow y'' = \left( {y'} \right)' = 6\end{array}\)
Câu hỏi 29 :
Khẳng định nào sau đây sai
- A \({\left( {\dfrac{1}{x}} \right)^\prime } = \dfrac{1}{{{x^2}}}\).
- B \({(\sqrt x )^\prime } = \dfrac{1}{{2\sqrt x }}\), với \(x > 0\)
- C \({\left( {{x^n}} \right)^\prime } = n{x^{n - 1}}\). với \(n\) nguyên dương
- D \({(c)^\prime } = 0\), với \(c\) hằng số
Đáp án: A
Phương pháp giải:
Xét từng đáp án.
Lời giải chi tiết:
\(\left( {\dfrac{1}{x}} \right)' = - \dfrac{1}{{{x^2}}}\)
Câu hỏi 30 :
Đạo hàm của hàm số \(y = \tan x - \cot x\) là
- A \(\dfrac{1}{{{{\sin }^2}x \cdot {{\cos }^2}x}}\).
- B \( - \tan x + \cot x\)
- C \(\dfrac{{ - 1}}{{{{\sin }^2}x \cdot {{\cos }^2}x}}\)
- D 1
Đáp án: A
Phương pháp giải:
\(\begin{array}{l}\left( {\tan x} \right)' = \dfrac{1}{{{{\cos }^2}x}}\\\left( {\cot x} \right)' = - \dfrac{1}{{{{\sin }^2}x}}\end{array}\)
Lời giải chi tiết:
\(y' = \dfrac{1}{{{{\cos }^2}x}} + \dfrac{1}{{{{\sin }^2}x}} = \dfrac{1}{{{{\sin }^2}x.{{\cos }^2}x}}\)
Câu hỏi 31 :
Hình lăng trụ đứng có đáy là hình chữ nhật có bao nhiêu mặt là hình chữ nhật ?
- A 4
- B 5
- C 6
- D 3
Đáp án: C
Phương pháp giải:
Hình lăng trụ đứng có cạnh bên vuông góc với đáy.
Lời giải chi tiết:
Hình lăng trụ đứng có đáy là hình chữ nhật là hình hộp chữ nhật nên có 6 mặt là hình chữ nhật.
Câu hỏi 32 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a,SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Góc giữa đường thẳng SC và mặt phẳng \((ABCD)\) bằng
- A
\(45^0\).
- B
\(90^0\).
- C
\(30^0\).
- D
\(60^0\).
Đáp án: D
Phương pháp giải:
Xác định hình chiếu của SC lên (ABCD).
Tính góc giữa SC và hình chiếu.
Lời giải chi tiết:
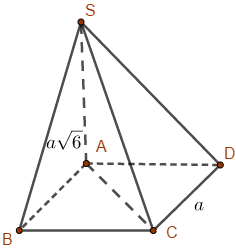
ABCD là hình vuông cạnh a nên \(AC = a\sqrt 2 \)
Ta có \(SA \bot (ABCD)\) nên AC là hình chiếu của SC lên (ABCD). Vậy góc giữa SC và (ABCD) là góc giữa SC và AC và bằng \(\widehat {SCA}\)
\(\begin{array}{l}\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 6 }}{{a\sqrt 2 }} = \sqrt 3 \\ \Rightarrow \widehat {SCA} = 60^\circ \end{array}\)
Câu hỏi 33 :
Cho hình chóp S.ABCD có SB vuông góc với mặt phẳng đáy. Mặt phẳng \((ABCD)\) vuông góc với mặt phẳng nào dưới đây?
- A (SAC)
- B (SBD)
- C (SCD)
- D (SAD)
Đáp án: B
Phương pháp giải:
Mặt phẳng chứa đường thẳng vuông góc với (ABCD) thì mặt phẳng đó vuông với (ABCD).
Lời giải chi tiết:
(SBD) chứa SB vuông góc với (ABCD) nên (SBD) vuông góc với (ABCD).
Câu hỏi 34 :
Đạo hàm của hàm số \(y = {\tan ^2}x\) là
- A \(2\cot x\)
- B 2
- C \(\dfrac{{2\tan x}}{{{{\cos }^2}x}}\)
- D \(2\tan x\).
Đáp án: C
Phương pháp giải:
\(\left( {\tan x} \right)' = \dfrac{1}{{{{\cos }^2}x}}\)
\(\left( {{u^n}} \right)' = n.u'.{u^{n - 1}}\)
Lời giải chi tiết:
\(y' = 2.\tan x.\dfrac{1}{{{{\cos }^2}x}} = \dfrac{{2\tan x}}{{{{\cos }^2}x}}\)
Câu hỏi 35 :
Trong không gian cho hai vectơ \(\vec u,\vec v\) tạo với nhau một góc \({120^0},|\vec u| = 4\) và \(|\vec v| = 3\). Tích vô hướng \(\vec u,\vec v\) bằng
- A 3
- B \( - 6\).
- C 2 .
- D \(3\sqrt 3 \).
Đáp án: B
Phương pháp giải:
\(\vec a\vec b = |\vec a||\vec b|\cos (\vec a,\vec b)\)
Lời giải chi tiết:
\(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|\cos (\overrightarrow u ,\overrightarrow v ) = 4.3.\cos 120^\circ = - 6\)
Câu hỏi 36 :
Câu 1:
Tính \(\mathop {\lim }\limits_{x \to + \infty } \left( {x - \sqrt {{x^2} - 2x + 3} } \right)\)
Phương pháp giải:
Nhân liên hợp.
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left( {x - \sqrt {{x^2} - 2x + 3} } \right)\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{{x^2} - \left( {{x^2} - 2x + 3} \right)}}{{x + \sqrt {{x^2} - 2x + 3} }}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{2x - 3}}{{x + \sqrt {{x^2} - 2x + 3} }}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x\left( {2 - \dfrac{3}{x}} \right)}}{{x\left( {1 + \sqrt {1 - 2.\dfrac{1}{x} + \dfrac{1}{{{x^2}}}} } \right)}}\\ = \dfrac{2}{{1 + 1}} = 1\end{array}\)
Câu 2:
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{\sqrt {3x - 5} - 1}}{{x - 2}},{\rm{ khi }}x \ne 2}\\{2m - 1,{\rm{ khi }}\quad x = 2}\end{array}} \right.\). Tìm \(m\) để hàm số \(f(x)\) liên tục tại điểm \(x = 2\).
Phương pháp giải:
\(f\left( x \right)\) liên tục tại \({x_0}\)\( \Leftrightarrow f\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\)
Lời giải chi tiết:
\(\begin{array}{l}f\left( 2 \right) = 2m - 1\\\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt {3x - 5} - 1}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{3\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {\sqrt {3x - 5} + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{3}{{\left( {\sqrt {3x - 5} + 1} \right)}} = \dfrac{3}{2}\\ \Rightarrow 2m - 1 = \dfrac{3}{2} \Leftrightarrow m = \dfrac{5}{4}\end{array}\)
Câu hỏi 37 :
Câu 1:
Tính đạo hàm của hàm số \(y = (3x - 1)\sqrt {{x^2} + 1} \)
Phương pháp giải:
\(\begin{array}{l}\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}\\\left( {u.v} \right)' = u'v + v'u\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}y' = 3.\sqrt {{x^2} + 1} + \left( {3x - 1} \right).\dfrac{x}{{\sqrt {{x^2} + 1} }}\\ = \dfrac{{3.\left( {{x^2} + 1} \right) + 3{x^2} - x}}{{\sqrt {{x^2} + 1} }}\\ = \dfrac{{6{x^2} - x + 3}}{{\sqrt {{x^2} + 1} }}\end{array}\)
Câu 2:
Cho hàm số \(y = \dfrac{{x - 1}}{{2x - 3}}\) có đồ thị \((C)\). Viết phương trình tiếp tuyến của \((C)\) tại \(M\) thuộc (C) sao cho tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân.
Phương pháp giải:
Gọi điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\). Tiếp tuyến có hệ số góc là \(f'\left( {{x_0}} \right)\).
Đường thẳng tạo với 2 trục tọa độ tam giác vuông cân khi hệ số góc thỏa mãn \(\left| k \right| = 1\)
Lời giải chi tiết:
Gọi điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là tiếp điểm của tiếp tuyến tại M.
Khi đó: \(\left| {f'\left( {{x_0}} \right)} \right| = 1\)
\(\begin{array}{l}f'\left( x \right) = \dfrac{{1.\left( {2x - 3} \right) - 2\left( {x - 1} \right)}}{{{{\left( {2x - 3} \right)}^2}}}\\ = \dfrac{{ - 1}}{{{{\left( {2x - 3} \right)}^2}}}\\ \Rightarrow \left| {f'\left( {{x_0}} \right)} \right| = \dfrac{1}{{{{\left( {2{x_0} - 3} \right)}^2}}} = 1\\ \Leftrightarrow \left| {2{x_0} - 3} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 1\end{array} \right.\end{array}\)
\({x_0} = 2 \Rightarrow f'\left( {{x_0}} \right) = - 1;f\left( {{x_0}} \right) = 1\).
Tiếp tuyến: \(y = - \left( {x - 2} \right) + 1 = - x + 3\)
\({x_0} = 1 \Rightarrow f'\left( {{x_0}} \right) = - 1;f\left( {{x_0}} \right) = 0\)
Tiếp tuyến: \(y = - \left( {x - 1} \right) = - x + 1\)
Câu hỏi 38 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \). Cạnh bên SA vuông góc với đáy, \(SA = 2a\).
Câu 1:
Tính góc giữa SC và mặt phẳng \((ABCD)\).
Phương pháp giải:
Xác định hình chiếu của SC lên (ABCD).
Lời giải chi tiết:
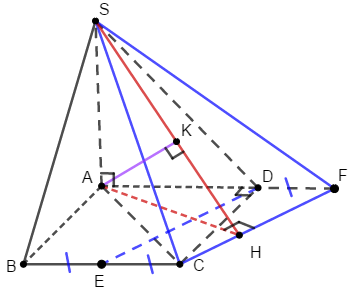
\(SA \bot \left( {ABCD} \right)\) nên AC là hình chiếu của SC lên (ABCD).
Góc giữa SC và (ABCD) bằng \(\widehat {SCA}\)
\(AC = a\sqrt 2 .\sqrt 2 = 2a\)
\(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = 1 \Rightarrow \widehat {SCA} = 45^\circ \)
Vậy góc giữa SC và (ABCD) là \(45^\circ \)
Câu 2:
Gọi \({\rm{E}}\) là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng DE và SC.
Phương pháp giải:
Xác định mặt phẳng (P) qua SC và song song với DE.
\(d\left( {SC,DE} \right) = d\left( {D,\left( P \right)} \right)\)
Tìm mối quan hệ \(d\left( {A,\left( P \right)} \right)\) và \(d\left( {D,\left( P \right)} \right)\).
Tìm hình chiếu của A lên (P).
Lời giải chi tiết:
Kẻ CF||DE ( F thuộc AD).
=> DE||(SCF)
=>d(DE,SC)=d(DE,(SCF))=d(D,(SCF)).
ECFD là hình bình hành nên
\(\begin{array}{l}DF = EC = \dfrac{{AD}}{2} \Rightarrow \dfrac{{AF}}{{DF}} = 3\\ \Rightarrow d\left( {D,\left( {SCF} \right)} \right) = \dfrac{1}{3}d\left( {A,\left( {SCF} \right)} \right)\end{array}\).
Kẻ \(AH \bot CF;AK \bot SH\)
\(\begin{array}{l}\left. \begin{array}{l} \Rightarrow CF \bot AH\\CF \bot SA\end{array} \right\} \Rightarrow CF \bot \left( {SAH} \right)\\ \Rightarrow CF \bot AK \Rightarrow AK \bot \left( {SCF} \right)\\ \Rightarrow d\left( {A,\left( {SCF} \right)} \right) = AK\\\tan \widehat {HFA} = \tan \widehat {CFD} = \dfrac{{DC}}{{DF}} = 2\\ \Rightarrow AH = 2HF\\ \Rightarrow A{H^2} + \dfrac{{A{H^2}}}{4} = A{F^2} = {\left( {\dfrac{3}{2}.a\sqrt 2 } \right)^2}\\ \Rightarrow \dfrac{5}{4}A{H^2} = \dfrac{{9{a^2}}}{2} \Rightarrow A{H^2} = \dfrac{{18{a^2}}}{5}\\\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}}\\ = \dfrac{5}{{18{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{19}}{{36{a^2}}}\\ \Rightarrow AK = \dfrac{{6a}}{{\sqrt {19} }}\\ \Rightarrow d\left( {SC,DE} \right) = \dfrac{{6a}}{{\sqrt {19} }}\end{array}\)
