Đề bài
Từ một điểm P nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến PA, PB đến (O) ( A, B là hai tiếp điểm). Trên dây AB lấy M bất kì. Qua M kẻ đường vuông góc với OM cắt PA tại S và PB tại Q. Chứng minh rằng: \(MS = MQ\).
Phương pháp giải - Xem chi tiết
Sử dụng:
+Tính chất tiếp tuyến
+Hai góc nội tiếp cùng chắn 1 cung thì bằng nhau
+Hai góc cùng bù 1 góc thì bằng nhau
Ta chứng minh: OM vừa là đường cao, vừa là đường phân giác trong tam giác OPQ nên OPQ là tam giác cân.
Lời giải chi tiết
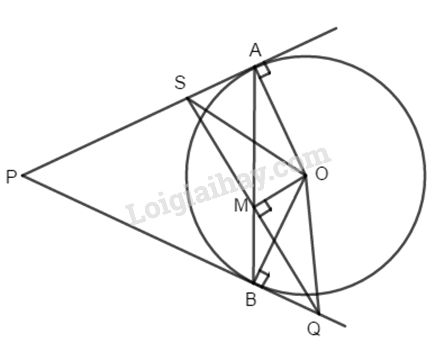
Ta có \(PA \bot OA\) hay \(SA \bot OA\) ( tính chất tiếp tuyến)
\(\Rightarrow \widehat {SAO} = 90^\circ \) nên A thuộc đường tròn đường kính SO.
\(OM \bot SQ\) (gt) \(\Rightarrow \widehat {SMO} = 90^\circ \) nên M thuộc đường tròn đường kính SO.
Suy ra 4 điểm S, A, O, M cùng thuộc đường tròn đường kính SO.
Xét đường tròn đường kính SO có \(\widehat {SAM} = \widehat {SOM}\) (1) (2 góc nội tiếp cùng chắn cung SM)
Xét tứ giác MOQB có \(\widehat {MOQ} = \widehat {OBQ} = {90^0}\) nên M và B là 2 đỉnh kề nhau cùng nhìn cạnh OQ dưới 1 góc vuông nên tứ giác MOQB là tứ giác nội tiếp.
Suy ra \(\widehat {MOQ} = \widehat {PBA}\) (2) (cùng bù với góc MBQ)
Lại có PA=PB (tính chất 2 tiếp tuyến cắt nhau) nên tam giác PAB cân tại P.
Suy ra \(\widehat {PAB} = \widehat {PBA}\) (3) (tính chất tam giác cân)
Từ (1), (2) và (3) suy ra \(\widehat {POM} = \widehat {MOQ}\) hay OM là tia phân giác góc POQ.
Như vậy OM vừa là đường cao, vừa là đường phân giác trong tam giác OPQ nên OPQ là tam giác cân.
Từ đó OM cũng là đường trung tuyến của tam giác OPQ nên suy ra MP=MQ (đpcm).
soanvan.me
