Đề bài
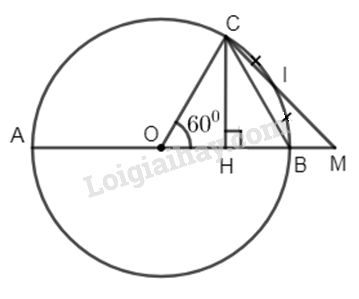
Cho đường tròn (O; R) đường kính AB. Lấy C thuộc đường tròn sao cho\(\widehat {COB} = 60^\circ \). Gọi I là điểm chính giữa của cung CB và M là giao điểm của OB và CI.
a) Tính \(\widehat {CMO}\).
b) Kẻ đường cao AH của ∆COM. Tính độ dài OM theo R.
Phương pháp giải - Xem chi tiết
Sử dụng:
+Số đo của góc ở tâm bằng số đo của cung bị chắn
+Số đo góc có đỉnh bên ngoài đường tròn
+Trong tam giác đều đường cao đồng thời là đường trung tuyến
+Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền nhân sin góc đối
Lời giải chi tiết
a) Ta có : \(sd\overparen{COB} = {60^o}\) (gt)
\( \Rightarrow sd\overparen{CB} = {60^o}\)
Do đó \(sd\overparen{AC} = 180^o - 60^o = 120^o\)
I là điểm chính giữa cung CB nên
\(sd\overparen{IC} = sd\overparen{IB} = \dfrac{{sdCB}}{2} = {30^o}\)
Vậy \(\widehat {CMO} = \dfrac{{sdAC - sdIB}}{2}\)\(\, = \dfrac{{{{120}^o} - {{30}^o}}}{2} = {45^o}\) ( góc có đỉnh bên ngoài đường tròn).
b) \(∆OCB\) cân có \(\widehat {COB} = 60^\circ \) nên là tam giác đều.
Do đó đường cao CH đồng thời là đường trung tuyến
Hay \(HO = HB = \dfrac{R }{2}\) và \(CH = OC.\sin 60^\circ = \dfrac{{R\sqrt 3 } }{2}.\)
Tam giác CHM vuông có \(\widehat {CMO} = 45^\circ \) (cmt) nên là tam giác vuông cân
\(\Rightarrow HM = CH = \dfrac{{R\sqrt 3 }}{2}.\)
Do đó\(OM = OH + HM = \dfrac{R}{2} +\dfrac {{R\sqrt 3 } }{ 2}\)\(\, = \dfrac{{R\left( {1 + \sqrt 3 } \right)} }{ 2}.\)
soanvan.me
